
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы механического подобияСодержание книги
Поиск на нашем сайте
Полученные на модели результаты опытных исследований обобщаются и затем переносятся на натуру. Выполнение этой процедуры требует знаний законов, связывающих между собой величины, полученные при исследованиях на модели, и соответствующие им величины в натуре. Эти законы называются законами подобия. Они устанавливают определенные соотношения между геометрическими размерами, кинематическими и динамическими характеристиками потоков в модели и натуре. Законы подобия подробно изучаются в специальных курсах теории подобия и моделирования. Следует отметить, что теория подобия имеет большое теоретическое и практическое значение не только для моделирования различных явлений и процессов, но и прежде всего для научного обоснования экспериментальных исследований, обработки их результатов и построения на их основе рациональных эмпирических формул. Следует иметь в виду, что динамическое или вообще физическое подобие является обобщением геометрического подобия. Рассмотрим способы получения масштабных коэффициентов для геометрического, кинематического и динамического подобия.
Геометрическое подобие Пусть имеем натурный объект (поток) (рис. 7.1), подлежащий гидродинамическому исследованию, и его модель.
Рис. 7.1 Обозначим геометрические размеры объекта (натурного потока) индексом 1, а модельного – индексом 2. Чтобы получить область течения в модели, геометрически подобную натурному потоку, разделим все линейные размеры натурного потока на некоторое число k, которое называется линейным масштабом. Таким образом получаем связь между геометрическими размерами а 1 и а 2, b 1 и b 2, в виде равенств:
Линейные размеры, связанные соотношением (7.1), называют соответственными, или сходственными. Точки, координаты которых удовлетворяют этому соотношению, называют сходственными. Безразмерные координаты сходственных точек одинаковы. Обычно за единицу измерения всех линейных величин в соответствующих потоках принимают L 1 (натура), L 2 (модель) и находят линейный масштаб kl:
Для площадей и объемов соответственно имеем:
Очевидно, что для геометрических подобных потоков необходима пропорциональность соответствующих площадей и объемов.
Кинематическое подобие Кинематическое подобие обязательно включает в себя геометрическое подобие, т.е. для кинематического подобия необходимо, чтобы траектории частиц обоих потоков были подобны геометрически. Кроме того, для кинематически подобных потоков отрезки траекторий соответствующих частиц натурного и модельного потоков, а также отрезки времени, в течение которых протекают соответствующие процессы в натуре и в модели, должны быть пропорциональны. Другими словами, если в первом потоке (натуре) частицы проходят путь L 1 за время t 1, то во втором потоке (модели) – путь L 2 за t 2. Причем, отрезки L 1 и L 2 должны быть геометрически подобны, а отношение Отношение
Тогда
Очевидно, что
Аналогично находим масштаб ускорений:
Таким образом, скорости и ускорения в сходственных точках потока связаны соотношениями
Динамическое подобие Динамическое подобие обязательно включает в себя геометрическое и кинематическое подобия. В любых потоках, если физическая природа действующих на жидкость сил одинакова и силы образуют геометрически подобные силовые многоугольники, они являются динамически подобными. В динамически подобных потоках отношение одноименных сил в сходственных точках в натуре и на модели постоянны, т.е.
К силам, действующим в потоке жидкости, можно отнести: силы внутреннего трения жидкости, силы тяжести, силы поверхностного натяжения и др. Для динамически подобных потоков отношение плотностей жидкости в натуре и на модели должно быть постоянным:
Обозначим действующие в сходственных точках натурного и модельного потоков силы Р 1 и Р 2 соответственно. По основному уравнению динамики, известному из теоретической механики, сила равна произведению массы на ускорение:
Учитывая, что масса равна произведению плотности на ее объем
где тогда
Ускорение определяется приращением скорости Следовательно,
Таким образом, для динамического подобия необходимо, чтобы силы находились в соотношении
Выражение (7.8) является математическим выражением общего закона динамического подобия, впервые сформулированным Ньютоном. Преобразуем выражение (7.8) к виду
Следовательно, В гидродинамических исследованиях во многих случаях оказывается невозможным найти количественные оценки действующих внешних сил, а следовательно, и их равнодействующей. Поэтому при исследованиях гидравлических явлений часто выделяют только одну силу, а действием остальных пренебрегают. В этом случае применяют частные критерии Рейнольдса, Фруда, Вебера и др.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.102.136 (0.01 с.) |


 . (7.1)
. (7.1) . (7.2)
. (7.2)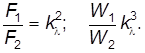 (7.3)
(7.3) должно быть одинаковым для сходственных точек обоих потоков.
должно быть одинаковым для сходственных точек обоих потоков.
 .
.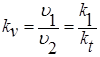 .
. .
.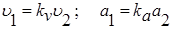 . (7.4)
. (7.4) , (7.5)
, (7.5)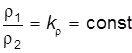 . (7.6)
. (7.6)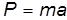 ,
,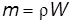 ,
, ,
,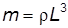 .
.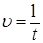 в единицу времени t, т.е.
в единицу времени t, т.е. 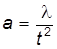 .
.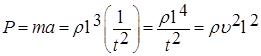 . (7.7)
. (7.7) . (7.8)
. (7.8)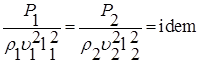 . (7.9)
. (7.9)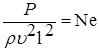 – критерий Ньютона. Критерий Ньютона является обобщенным критерием динамического подобия механических систем.
– критерий Ньютона. Критерий Ньютона является обобщенным критерием динамического подобия механических систем.


