
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная теорема гидростатикиСодержание книги
Поиск на нашем сайте
Гидростатическое давление в данной точке не зависит от направления, т.е. остается одинаковым по всем направлениям. Докажем, что рх = ру = р z = р n, где рх, р y, р z, р n –представляют собой гидростатическое давление соответственно в направлении координатных осей ox, oy, oz и в некотором произвольном направлении N- N (рис. 2.2).
Рис. 2.2 Выделим внутри массы жидкости, находящейся в равновесии, малый объем в форме тетраэдра с ребрами dx, dy, dz, соответст-венно параллельными координатным осям, и с массой dm =
Представим, что жидкость внутри тетраэдра – в виде твердого тела. Это не изменяет условий равновесия. Воспользуемся известными уравнениями статики твердого тела, а именно уравнениями проекций сил и уравнениями моментов:
Учитывая, что при стягивании тетраэдра в точку, уравнения моментов такой системы удовлетворяются тождественно, а действующие на него силы сводятся к системе сил, проходящих через одну и ту же точку. Таким образом, остается только три проекции сил:
К действующим силам относятся поверхностные и массовые (объемные) силы. К поверхностным силам относятся силы давления жидкости, окружающей элементарный тетраэдр. Таких сил будет четыре (по числу граней). На грань АВС действует сила
Сила dPx параллельна оси ox, направлена в противоположную сторону оси и, следовательно, войдет в уравнение со знаком «плюс». Силы dPy и dPz,действующие на грани ABD и ACD, соответственно параллельны осям oy и oz и их проекции на ось ox равны нулю. Четвертая сила dPn – сила давления на грань ВС D равна:
Произведение d wcos(N, ox) представляет собой проекцию площади треугольника BCD на плоскость у oz и равно:
Тогда проекция силы dPn на ось ox численно равна:
Аналогично можно записать проекции силы dPn на оси oy и oz:
Массовые силы, действующие на тетраэдр, приводятся к равнодействующей dR, образующей с координатными осями углы a, b, g и равной:
Обозначим проекции ускорения j по координатным осям x, y, z, т.е. примем, что
Тогда проекции объемной силы dR равны:
Запишем сумму проекций всех сил на ось ox с учетом уравнений (2.12):
Или после сокращения на
Пренебрегая Аналогично py = pn и pz = pn. Следовательно, px = py = pz = pn. (2.14) Что и надо было доказать. Таким образом, гидростатическое давление в точке по любому направлению оказывается одинаковым, т.е. не зависит от направления действия.
2.4. Условие равновесия жидкости Жидкость может сохранять свое равновесное состояние в том случае, если внешние силы, действующие в точках граничной поверхности, направлены только по внутренним нормалям к этой поверхности. Очевидно, что действие силы давления по внешней нормали приводит к нарушению равновесия, т.к. жидкость не оказывает сопротивления растягивающим силам. Касательные силы возникают при движении жидкости, поэтому при равновесии жидкости, находящейся в покое, они равны нулю. Следствие. Так как гидростатическое давление одинаково по всем направлениям в данной точке, а в различных точках данного объема жидкости в общем случае различно, то
В общем случае, когда изменяется атмосферное давление во времени:
2.5. Дифференциальное уравнение равновесия жидкости (Уравнение Эйлера) Выделим в жидкости элементарный параллелепипед ABCDA ¢ B ¢ C ¢ D ¢ (рис. 2.3). Полагая его твердым телом, составим три уравнения проекций действующих сил:
Рис. 2.3 Уравнение моментов исключается. Составим уравнение проекции сил на ось ox, т.е. уравнение Равновесие параллелепипеда обеспечивается шестью проекциями (по числу граней). В уравнение Сила давления на грань ABCD
Сила давления на грань A ¢ B ¢ C ¢ D ¢
Определим р ¢. Так как p = f(x, y, z), то при переходе от одной грани к другой давление должно изменяться в зависимости от одной координаты, так как в сходственных точках (A и A ¢, B и B ¢ и т.д.) давление зависит только от изменения одного аргумента x. Аргументы y и z для сходственных точек (А и А ¢) остаются неизменными. Следовательно
Тогда
Сила dP ¢войдет в уравнение проекции со знаком «минус». Проекции объемных сил. Проекция объемной силы dR равна произведению массы на соответствующую проекцию ускорения объемной силы, т.е.
Сумма проекций поверхностных и объемных сил на ось Ох равна:
После некоторого преобразования и деления на dxdydz (объем параллелепипеда dW) получим уравнение проекций сил на ось Ох, отнесенных к единице объема:
Аналогично получим два других уравнения: Таким образом, при равновесии жидкости имеем три дифферен-циальных уравнения:
Система уравнений (2.19) равновесия жидкости относится как к несжимаемой, так и к сжимаемой жидкости. Эта система уравнений впервые была получена Эйлером в 1755 г.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |


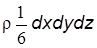 ,
,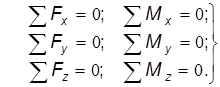 (2.3)
(2.3)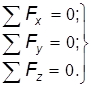 (2.4)
(2.4)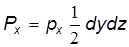 , (2.5)
, (2.5)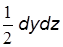 .
.
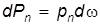 , (2.6)
, (2.6) Проекция этой силы на ось ox:
Проекция этой силы на ось ox:
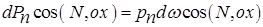 . (2.7)
. (2.7) Эта сила направлена в отрицательную сторону оси ox.
Эта сила направлена в отрицательную сторону оси ox.
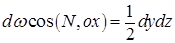 . (2.8)
. (2.8)
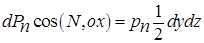 . (2.9)
. (2.9)

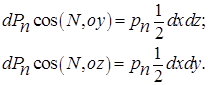 (2.10)
(2.10) , (2.11)
, (2.11)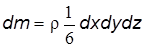 ,
,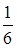 dxdydz –
dxdydz –
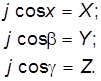
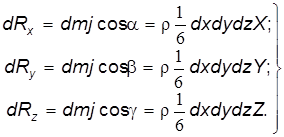 (2.12)
(2.12)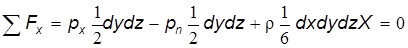 . (2.13)
. (2.13)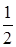 dydz:
dydz: .
.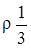 dxX как бесконечно малым относительно px и pn, получаем px – pn = 0или px = pn.
dxX как бесконечно малым относительно px и pn, получаем px – pn = 0или px = pn.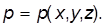 (2.15)
(2.15)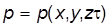 . (2.16)
. (2.16)
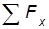 =0;
=0; 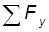 =0;
=0; 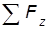 =0.
=0.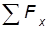 = 0.
= 0.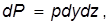
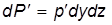 ,
,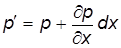 .
.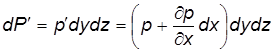 .
.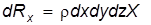 ,
, . (2.17)
. (2.17)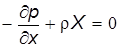 . (2.18)
. (2.18)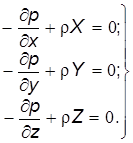 (2.19)
(2.19)


