
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приборы для измерения давленияСодержание книги
Поиск на нашем сайте
Приборы К приборам жидкостного типа относятся: пьезометр, ртутные манометры, поршневые манометры, дифференциальные манометры, микроманометры, вакуумметры. К приборам механического типа относятся пружинные и мембранные манометры. Простейшим прибором жидкостного типа является пьезометр (рис. 2.17).
Рис. 2.17 Пьезометр представляет собой стеклянную трубку диаметром не менее 5 мм, открытую с одного конца. Второй конец трубки присоединен к сосуду, в котором измеряется давление. При р 0 > р атм на свободной поверхности жидкости в сосуде жидкость в пьезометре поднимается выше уровня в сосуде на некоторую высоту h п. Гидростатическое давление в точке А на глубине h от свободной поверхности определяется по основному уравнению гидростатики:
Отсюда
Учитывая, что
находим
Таким образом, пьезометрическая высота характеризует избыточное давление в сосуде и может быть мерой для определения его значения. Измерение давления пьезометрами весьма удобно и часто применяется в технике измерений, так как пьезометр очень чувствительный и точный прибор. При измерении давления надо иметь в виду следующие соотношения: давление в 1Па соответствует 0,0075 мм рт. ст. или 0,102 мм вод. ст. Пьезометры применяются при измерении небольших давлений, так как высота трубки пьезометра ограничена. При более высоких давлениях используют жидкостные манометры, в которых давление уравновешивается не жидкостью, находящейся в сосуде, а жидкостью большей плотности, например, ртутью, так как ее плотность в 13,6 раза больше плотности воды. Ртутный манометр (рис. 2.18) представляет U - образную стеклянную трубку, изогнутое колено которой заполняется ртутью.
Рис. 2.18 Давление жидкости p 0 в сосуде уравновешивается столбом ртути h рт. Для точки А имеем
Для точки В
Для измерения высоких давлений применяют поршневой манометр (рис. 2.19), представляющий собой обращенный гидравлический пресс.
Поршневой манометр состоит из входной трубки 1 для входного давления r0, поршня 2, металлической пластины 3, резиновой диафрагмы 4, соприкасающейся с водой, короткого колена манометра 5, открытой трубки 6, которые заполнены ртутью.
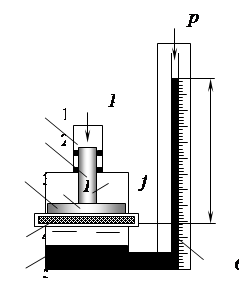
Рис. 2.19 Обозначая площадь поршня f, площадь металлической пластины F, высоту ртути в манометрической трубке h, найдем выражение для определения давления p 0 согласно уравнению равновесия:
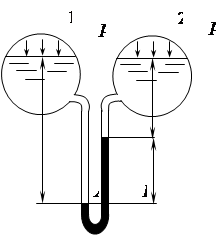
Видно, что поршневой манометр при сравнительно малой высоте ртутного столба позволяет измерять весьма высокие давления. Для измерения разности давления в двух сосудах применяется дифференциальный манометр (рис. 2.20).
Рис. 2.20 Он также используется при измерении разности давления в двух точках жидкости в одном и том же сосуде. Давление в левом колене в точке А
Отсюда
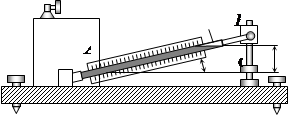
т.к. Микроманометры используются при измерении низких давлений с повышенной точностью. Микроманометры с наклонной шкалой представлены на рис. 2.21.
Рис. 2.21 Манометр состоит из резервуара А, присоединенного к сосуду, в котором измеряется давление, и манометрической трубки В, угол наклона которой к горизонту a можно изменять. Давление у основания трубки определяется выражением:
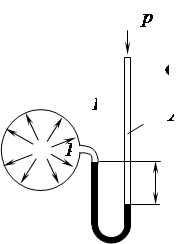
Для измерения вакуума служат приборы, называемые вакуумметрами. Вакуумметр (рис. 2.22) представляет собой изогнутую трубку.
Рис. 2.22 Конец трубки А присоединен к сосуду В, в котором измеряется вакуум. Трубка с открытым концом сообщается с атмосферой. Применяя основное уравнение гидростатики p = p атм – rрт× qh рт, находим высоту h рт = Применение рассмотренных приборов жидкостного типа ограничивается областью сравнительно невысоких давлений. В основном, их используют в лабораторной практике. Для измерения высоких давлений применяют механические приборы. Существуют два типа приборов: пружинные и мембранные.
2.15. Равновесие тела в покоящейся жидкости.
Определим силу давления со стороны жидкости на погруженное в нее тело (рис. 2.23). Рассмотрим тело, погруженное в жидкость объемом W и плотностью Плотность жидкости r. Поверхностные силы
Рис. 2.23 Вертикальные силы давления, действующие на поверхности АВ и СD, равны весу жидкости в объеме соответствующего тела давления:
Равнодействующая этих сил
Сила Р называется Архимедовой силой и направлена вверх. Формула (2.89) отражает закон Архимеда: на погруженное в жидкость тело действует выталкивающая сила, равная весу вытесненной им жидкости. Силу Р называют взвешивающей силой, подъемной силой или водоизмещением, а точку ее приложения к телу, соответствующую центру давления, называют центром водоизмещения. При полном погружении тела в однородную жидкость сила Р зависит не от глубины погружения, а только от плотности жидкости (если r = const) и от объема тела W. Линия действия Архимедовой силы Р проходит через центр тяжести объема вытесненной жидкости W i. Рассмотрим условия равновесия плавающих тел. Условия равновесия погруженного в жидкость тела определяются характером погружения тела и соотношением действующих на тело вертикальных сил: веса тела
При полном погружении однородного тела ( 1) Следовательно, тело тонет, т.е. равнодействующая сил направлена вниз. 2) В этом случае тело находится в состоянии безразличного равновесия. Равнодействующая сил равна нулю. 3) Тело всплывает на поверхность жидкости. Равнодействующая сил направлена вверх. Все вышеизложенное относится и к подводному плаванию неоднородного тела с той лишь разницей, что центр тяжести его будет лежать ниже центра водоизмещения. Вес жидкости в объеме погруженной части тела называется водоизмещением, а центр тяжести этого объема D – центром водоизмещения (рис. 2.24).
Рис. 2.24 Линия А-А называется ватерлинией, а внутренняя часть – плоскостью плавания. Линия О-О является осью плавания. Расстояние CD называется эксцентриситетом. Способность плавающего тела восстанавливать начальное положение после воздействия внешней силы называется остойчивостью (рис. 2.25).
Рис. 2.25. Тогда
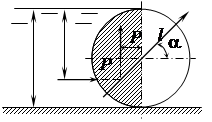
Примеры Пример 1. Определить силу, точку приложения и направление ее действия, если вода действует на затвор диаметром D = 2 м, шириной В = 3 м (рис. 2.26).
Рис. 2.26 Решение: 1. Cила, действующая на вертикальную проекцию,
2. Вертикальная составляющая силы
3. Полная сила гидростатического давления
4. Угол наклона результирующей силы с горизонтальной осью
Сила Р проходит через центр окружности и приложена в точке D.
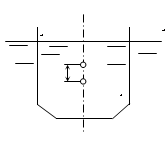
Пример 2. Определить плотность шара r, плавающего в сосуде, при полном погружении, если центр тяжести шара лежит в плоскости раздела жидкостей r1 = 1000 кг/м3 и r2 = 1200 кг/м3 (рис.2.27).
Рис.2.27 Решение: Обозначим объем шара 2 W. Так как центр шара находится в плоскости раздела, то ясно, что он вытеснил равные объемы W каждой из жидкостей. Очевидно, что на шар действуют выталкивающие силы:
После сокращения на
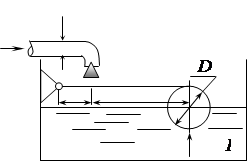
Пример 3. Определить минимально необходимый диаметр шарового поплавка, обеспечивающего автоматическое закрытие клапана при наполнении резервуара, если вода под давлением Cобственной массой рычага, клапана и поплавка пренебречь (рис. 2.28).
Рис. 2.28 Решение: 1. Сила, действующая на клапан:
2.Подъемная сила, приложенная к шару:
3. Необходимый объем поплавка:
4.Диаметр шара:
Контрольные вопросы 1. По каким формулам определяется сила давления и центр давления на цилиндрические поверхности? 2. Что такое тело давления? Как определяется тело давления при отсутствии свободной поверхности? 3. Как определяется давление жидкости в круглой трубе? 4. По какой формуле определяется сила гидростатического давления жидкости на колено трубы? 5. Как формулируется закон Архимеда? 6. Что такое остойчивость плавающего тела? 7. Что называется метацентром и метацентрическим радиусом?
3.1. Основные понятия и определения Кинематика жидкости изучает связь между геометрическими характеристиками движения и времени (скоростью и ускорением). Динамика жидкости (или гидродинамика) изучает законы движения жидкости как результат действия сил. Классификация видов движения жидкости основана на ряде признаков. По характеру протекания процесса: 1. Неустановившееся движение жидкости – движение, изменяющееся во времени, т.е. скорость и давление в данной точке изменяются с течением времени. Иллюстрацией неустановившегося движения жидкости может быть истечение из резервуара при его опорожнении. 2. Установившееся движение жидкости – это такое, при котором в любой точке пространства скорость и давление не изменяются ни по направлению, ни по величине.
Установившееся движение может быть равномерным и неравномерным. Равномерным движением называется такое, при котором скорости в сходственных точках двух смежных сечений равны между собой, а траектории частиц – прямолинейны и параллельны оси ох, т.е. поле скоростей не изменяется вниз по течению. Ускорение частиц жидкости при этом равно нулю. В символической форме это условие можно записать Неравномерное движение – это движение, не удовлетворяющее определению равномерного движения, т.е. Равномерное и неравномерное движение может быть напорным и безнапорным. При напорном жидкость соприкасается с твердой стенкой (р > р атм) по всему периметру своего сечения, а при безнапор- При поступательном движении частиц жидкости наблюдается их вращательное движение. Такое движение называется вихревым. Поступательное движение в направлении одной координаты называется одномерным движением жидкости.
Если параметры жидкости при движении изменяются в направлении двух координат, то движение называется двухмерным: При изменении параметров жидкости по трем координатам движение называется трехмерным:
или
Прикладная механика жидкости и газа занимается одномерным движением жидкости при решении практических задач.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.66 (0.009 с.) |

 для измерения гидростатического давления можно подразделить на две группы: жидкостные и механические.
для измерения гидростатического давления можно подразделить на две группы: жидкостные и механические.

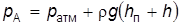 .
. .
.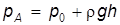 ,
,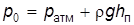 .
.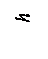
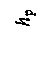

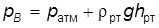 . Так как pА = pВ, приравнивая выражения правой части уравнений, получим
. Так как pА = pВ, приравнивая выражения правой части уравнений, получим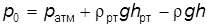 ,
,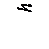
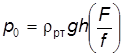 .
.

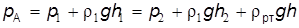 .
.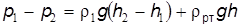 или
или 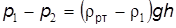 ,
, .
.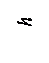
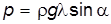 ,
,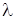 –
–
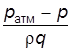 , соответствующую вакууму в сосуде, которую обычно называют вакуумметрической высотой и обозначают h вак.
, соответствующую вакууму в сосуде, которую обычно называют вакуумметрической высотой и обозначают h вак.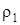 .
. и
и 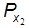 взаимно уравновешены.
взаимно уравновешены.

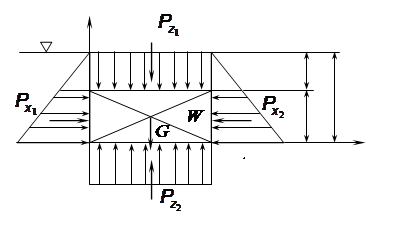
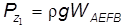 и
и 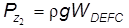 ,
,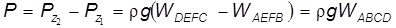 . (2.89)
. (2.89)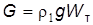 и архимедовой силы:
и архимедовой силы: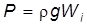 ,
,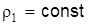 )
)  под уровень свободной поверхности
под уровень свободной поверхности 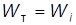 центр водоизмещения совпадает с центром тяжести тела, а силы G и P направлены по одной вертикали. Можно выделить три случая:
центр водоизмещения совпадает с центром тяжести тела, а силы G и P направлены по одной вертикали. Можно выделить три случая: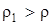 или G-P =
или G-P = 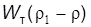 > 0,т.е. G > P.
> 0,т.е. G > P.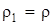 или G-P =
или G-P = 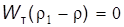 , т.е. G = P.
, т.е. G = P.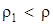 или G-P =
или G-P = 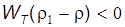 , т.е. P > G.
, т.е. P > G.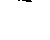
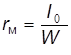

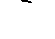

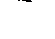

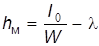 ;
;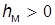 – плавание остойчивое и
– плавание остойчивое и 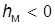 – неостойчивое.
– неостойчивое.
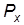 :
: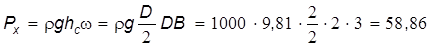 кН.
кН.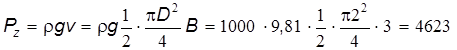 кН.
кН.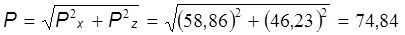 кН.
кН. .
.
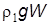 верхней его половины и
верхней его половины и 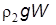 нижней половины. В равновесии алгебраическая сумма силы тяжести
нижней половины. В равновесии алгебраическая сумма силы тяжести 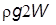 и архимедовых сил равна нулю, т.е.
и архимедовых сил равна нулю, т.е.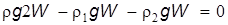 .
. получим
получим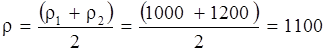 кг/м3.
кг/м3.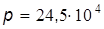 Па заполняет резервуар через трубу диаметром d = 15 мм, при а = 15 мм и b = 500 мм.
Па заполняет резервуар через трубу диаметром d = 15 мм, при а = 15 мм и b = 500 мм.
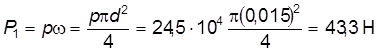 .
.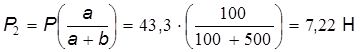 .
.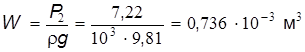 .
.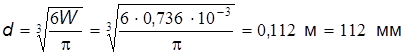 .
. 3. ОСНОВЫ КИНЕМАТИКИ И ДИНАМИКИ ЖИДКОСТИ
3. ОСНОВЫ КИНЕМАТИКИ И ДИНАМИКИ ЖИДКОСТИ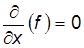 ; здесь (f) означает тот или иной параметр, например скорость, глубину h, путь
; здесь (f) означает тот или иной параметр, например скорость, глубину h, путь 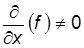 .
.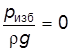 .
.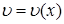 ; р = р (х) – установившееся одномерное движение жидкости;
; р = р (х) – установившееся одномерное движение жидкости;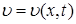 ; р = р (х, t) – неустановившееся одномерное движение жидкости.
; р = р (х, t) – неустановившееся одномерное движение жидкости.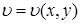 ; р = р (х, у) или
; р = р (х, у) или 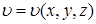 ; р = р (х, у, t).
; р = р (х, у, t).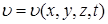 ; р = р(х, у, z, t).
; р = р(х, у, z, t).


