Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы исследования движения жидкости
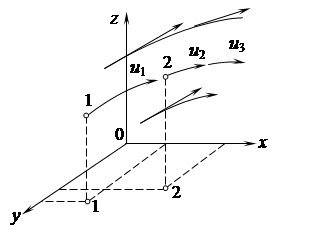
Существует два метода изучения движения жидкости: метод Лагранжа и метод Эйлера. Метод Лагранжа изучает изменение положения в пространстве отдельных частиц жидкости, т.е. траектории их движения. Метод Эйлера изучает поле скоростей, т.е. картину движения частиц жидкости в отдельных точках пространства в данный момент времени. Метод Лагранжа в гидродинамике используется редко, ввиду его сложности. Обычно изучение движения основано на методе Эйлера, суть которого заключается в следующем. Метод основан на понятии местной скорости или скорости в точке в данный момент времени. В общем случае местные скорости различны в один и тот же момент времени (рис. 3.8) в разных точках. Они могут изменяться во времени в каждой точке.
Рис. 3.8 Проекции скорости на оси координат можно записать в виде функций:
Функция (3.5) характеризует поле скоростей движущейся жидкости. Используя метод Эйлера, можно выразить ускорение а жидкой частицы в соответствии с физическим смыслом:
Если учесть, что для движущейся частицы ее координаты являются функциями времени:
то проекции скорости будут сложными функциями времени:
Используя правило дифференцирования сложных функций, для проекций полного ускорения получим:
Учитывая, что для движущейся жидкости
преобразуем функции (3.6) к виду:
Уравнение Эйлера По основному закону механики равнодействующая всех внешних сил, действующих на данное тело, равна массе тела, умноженной на ускорение, с которым движется это тело:
Выделим в потоке жидкости элементарный объем в форме параллелепипеда (рис. 3.9) и запишем основное уравнение (3.8) в проекциях по осям:
Рис. 3.9 Для первого уравнения (3.9) найдем массу
Ускорение вдоль оси Ох равно первой производной скорости по времени t, т.е.
Учитывая, что где получим
На выделенную элементарную массу действуют поверхностные силы давления и объемные силы (или массовые), т.е. в силу dRx включаются эти силы. Рассмотрим проекцию силы давления на боковую грань АВСD и А ¢ В ¢ С ¢ D ¢:
Тогда
Проекция объемной силы dFx определяется выражением:
Проекция равнодействующей с учетом выражений (3.10) и (3.11) имеет вид:
Подставляя выражение (3.9а) в уравнение (3.12), получим:
После сокращения на
Аналогично составив выражения для сил dRy и dRz и для dmay и dmaz, получим три уравнения Эйлера:
Система (3.14) описывает движение как капельной, так и газообразной жидкости. В системе 3-х уравнений пять неизвестных uх, uу, uz, p и r, поэтому необходимо иметь еще два уравнения. Такими уравнениями являются уравнения неразрывности и характеристическое уравнение. При
Контрольные вопросы 1. Что изучает кинематика и динамика жидкости? 2. Что представляет собой линия потока и траектория движения? В чем различие? 3. Что называется трубкой тока, элементарной струйкой и каковы их свойства? 4. Что называется потоком жидкости? 5. Что называется живым сечением, смоченным периметром и гидравлическим радиусом? 6. Что называется средней скоростью потока и расходом? 7. Напишите уравнение неразрывности (сплошности) потока. 8. Приведите примеры равномерного и неравномерного, напорного и безнапорного движения. 9. Что изучает метод Лагранжа? 10. Что изучает метод Эйлера? 3.9. Интегрирование уравнения Эйлера
При установившемся движении частные производные по времени равны нулю, т.е.
В этом случае движение жидкости может быть вихревым. Запишем уравнение Эйлера в следующем виде:
Умножим первое уравнение на dx, второе на dy и третье на dz; здесь dx, dy и dz являются проекциями элементарного перемещения. Тогда, для первого уравнения будем иметь:
Учитывая, что
где выражение в скобках представляет полный дифференциал проекции скорости на ось ox т.е.
С учетом уравнения (3.17) первое уравнение запишем в виде
Оставшиеся два уравнения записываются по аналогии:
Сложив почленно уравнения (3.17а, б, в), после некоторых преобразований получим:
Здесь u 2представляет полную скорость в данной точке. Левую часть уравнения можно представить в виде силовой функции U(x, y, z) и полного дифференциала dp, т.е.
и
тогда имеем
или
После интегрирования уравнения (3.18) получаем:
Выражение (3.19) называют интегралом Бернулли-Эйлера. Если движение жидкости протекает под действием только сил тяжести и жидкость несжимаемая, т.е.
С учетом выражений (3.20) интеграл Бернулли (3.19) принимает вид:
или после деления членов уравнения на g получим известное уравнение Бернулли в его обычной форме:
Для установившегося вихревого движения значение Н постоянно только вдоль одной линии тока или траектории (для элементарной струйки). Это следует из условий интегрирования для потенциальных течений. Уравнение Бернулли имеет большое практическое и теоретическое значение. Согласно уравнению Бернулли сумма трех высот остается неизменной вдоль данной элементарной струйки (рис 3.10). Высота z называется геометрической высотой, или высотой положения центра тяжести сечения струйки;
Рис. 3.10 Энергетический смысл уравнения Бернулли представляет собой полную энергию, отнесенную к единице веса жидкости. Сопоставляя основное уравнение гидростатики
Так как
В связи с этим уравнение Бернулли часто называют уравнением энергии.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 895; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.2.15 (0.024 с.) |
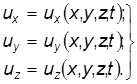 (3.5)
(3.5)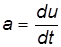 .
.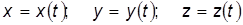 ,
,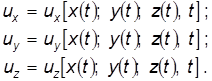
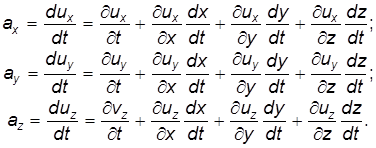 (3.6)
(3.6)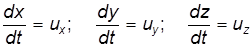 ,
,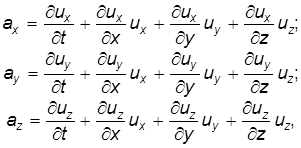 (3.7)
(3.7)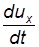 ;
; 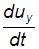 ;
; 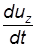 –
–
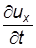 ;
; 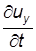 ;
; 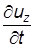 –
–
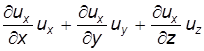 –
–
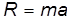 . (3.8)
. (3.8)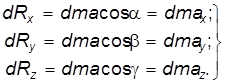 (3.9)
(3.9)

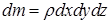 .
.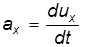 :
: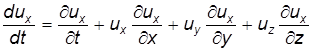 .
.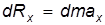 ,
,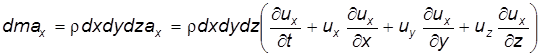 ,
,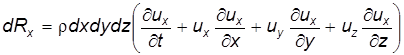 . (3.9а)
. (3.9а)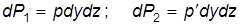 ,
,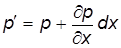 .
.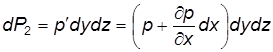 . Сила dP 2войдет в основное уравнение со знаком «минус», т.е. в сумму проекций сил давления на боковые грани:
. Сила dP 2войдет в основное уравнение со знаком «минус», т.е. в сумму проекций сил давления на боковые грани: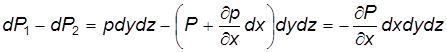 . (3.10)
. (3.10)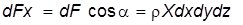 , (3.11)
, (3.11)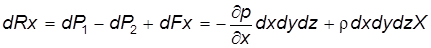 . (3.12)
. (3.12)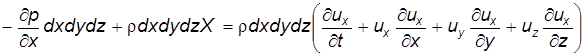 .
.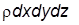 , т.е. отнеся уравнение к единице массы, получим:
, т.е. отнеся уравнение к единице массы, получим: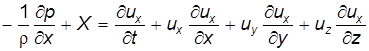 . (3.13)
. (3.13)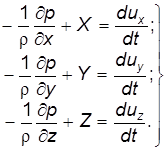 (3.14)
(3.14)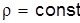 (для капельной жидкости) достаточно уравнения неразрывности:
(для капельной жидкости) достаточно уравнения неразрывности: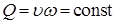 .
.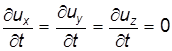 .
.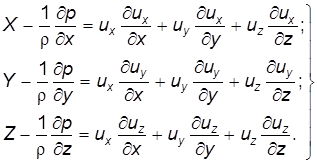 (3.15)
(3.15)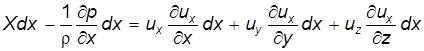 . (3.16)
. (3.16)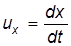 ;
; 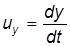 и
и 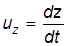 , преобразуем правую часть уравнения (3.16) к виду:
, преобразуем правую часть уравнения (3.16) к виду: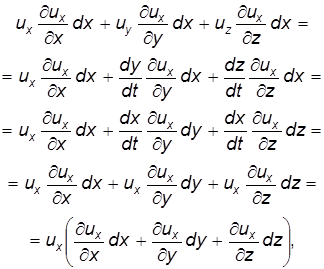
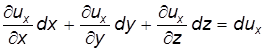 . (3.17)
. (3.17)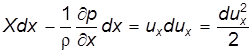 . (3.17а)
. (3.17а)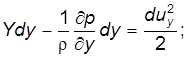 (3.17б)
(3.17б)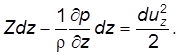 (3.17в)
(3.17в)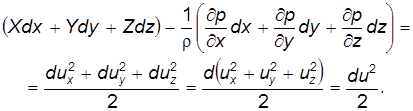
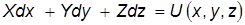
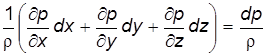 ;
;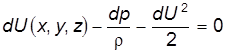
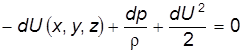 . (3.18)
. (3.18)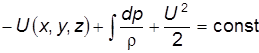 . (3.19)
. (3.19)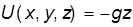 и
и 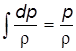 . (3.20)
. (3.20)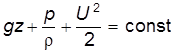
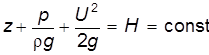 . (3.21)
. (3.21)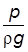 – высота, определяемая величиной гидродинамического давления, или пьезометрическая высота;
– высота, определяемая величиной гидродинамического давления, или пьезометрическая высота; 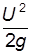 – скоростная высота, или скоростной напор.
– скоростная высота, или скоростной напор.
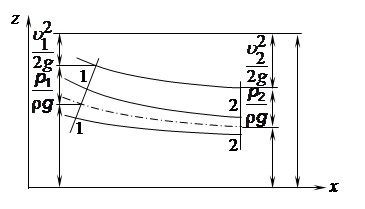

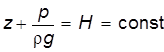 с уравнением Бернулли, видим, что слагаемое
с уравнением Бернулли, видим, что слагаемое 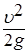 можно рассматривать как кинетическую энергию, отнесенную к единице веса жидкости:
можно рассматривать как кинетическую энергию, отнесенную к единице веса жидкости: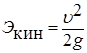 .
.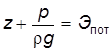 , то полный запас энергии элементарной струйки, отнесенной к весу жидкости, будет равен сумме:
, то полный запас энергии элементарной струйки, отнесенной к весу жидкости, будет равен сумме: