
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Организация статистического моделирования. Метод монте - карло.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КЛАССИФИКАЦИЯ МОДЕЛЕЙ Общие понятия моделирования. Прежде чем перейти к вопросу о классификации, определим понятия «модель» и «моделирование». В самом общем случае МОДЕЛЬ (от лат. - мера, образец) - упрощенное представление о реальном объекте, процессе или явлении. МОДЕЛЬ – это некоторый материальный или абстрактный объект или явление, замещающий оригинальный объект или явление, сохраняя только некоторые важные его свойства. Другими словами, МОДЕЛЬ – это объект или явление, в достаточной степени повторяющие свойства моделируемого объекта или явления (прототипа), существенные для целей конкретного моделирования, и опускающие несущественные свойства, в которых они могут отличаться от прототипа. МОДЕЛИРОВАНИЕ – исследование объектов познания на их моделях; построение и изучение моделей реально существующих предметов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя. Моделирование (в широком смысле) является основным методом исследований во всех областях знаний и научно обоснованным методом оценок характеристик сложных систем, используемым для принятия решений в различных сферах инженерной деятельности. ОСНОВНОЕ ТРЕБОВАНИЕ К МОДЕЛИ – это её адекватность (степень соответствия процессов, протекающих в модели, процессам, имеющих место, в системе, и, следовательно, степень соответствия свойств и характеристик модели свойствам и характеристикам системы). ГЛАВНЫЕ ФУНКЦИИ МОДЕЛИ - упрощение получения информации о свойствах объекта; передача информации и знаний; управление и оптимизация объектами и процессами; прогнозирование; диагностика. v Многообразие объектов исследования предопределяет использование для их изучения множества различных моделей. Способов классификации необычайно много. Приведем лишь некоторые, наиболее известные ВИДЫ МОДЕЛЕЙ И ПРИЗНАКИ ИХ КЛАССИФИКАЦИИ: ® Детерминированные и стохастические (по наличию случайного фактора) При моделировании сложных реальных систем исследователь часто сталкивается с ситуациями, в которых случайные воздействия играют существенную роль. Стохастические модели, в отличие от детерминированных, учитывают вероятностный характер параметров моделируемого объекта. Анализ стохастических моделей выполняется на компьютере на основе статистики, набираемой в ходе имитационных экспериментов при многократном прогоне модели для различных значений исходных случайных величин, выбранных в соответствии с их статистическими характеристиками. ® Динамические и статические (с учетом фактора времени) Статическая модель – это единовременный срез информации по данному объекту (модели, описывающие состояние системы в определенный момент времени). Пример: строение молекулы. Динамическая модель – представляет картину изменения объекта во времени. Примеры: описание движения тел, процесс химических реакций. ® Одномерные и многомерные (по числу переменных) Наличие параметров у матричной модели говорит о ее большей сложности и, возможно, точности по сравнению со скалярной. Например, если не выделить в населении страны все возрастные группы, рассматривая его изменение как целое, получим скалярную модель (например, модель Мальтуса), если выделить, - матричную (половозрастную). Именно матричная модель позволила объяснить колебания рождаемости после войны. ® Аналитические и численные (по характеру решений) Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат. Численная модель характеризуется зависимостью такого вида, который допускает только частные решения для конкретных начальных условий и количественных параметров моделей. ® Вычислительные и аналоговые (по характеру используемой ВТ) Аналоговые модели – при моделировании процессов на ВМ непрерывного действия (аналоговых или моделирующих машинах); вычислительные – при моделировании процессов на цифровых ВМ. ® Непрерывные и дискретные (для моделирования систем с дискретным и непрерывным состоянием) ® Физические, математические и др. (в зависимости от способа представления системы или от способа реализации модели). Физические модели – это «материальные» модели, эквивалентные или подобные в той или иной степени оригиналу. В общем случае физические модели – это модели, процесс функционирования которых такой же, как у оригинала, имеет ту же или подобную физическую породу. Математические модели – это «абстрактные» модели, представляющие собой формализованное описание изучаемой системы с помощью абстрактного языка, в частности, с помощью математических соотношений, отображающих процесс функционирования системы. ® Линейные и нелинейные Линейная модель – модель, отображающая состояние или функционирование системы таким образом, что все взаимозависимости в ней принимаются линейными, и, как следствие, она может формулироваться в виде одного линейного уравнения или СЛАУ. Нелинейная – модель, отображающая состояние или функционирование системы таким образом, что все взаимозависимости в ней принимаются нелинейными. Основная область применения нелинейных моделей – нелинейное программирование. Имеются и другие признаки классификации, например: по области использования (учебные, научно-технические, игровые), по степени адекватности (полные, приближенные), в зависимости от метода анализа (аналитические; имитационные - модель воспроизводит процесс функционирования системы во времени, причем модель имитирует все элементарные составляющие процесса с обязательным сохранением их взаимосвязанности и взаимообусловленности, логической структуры и последовательности протекания по времени; комбинированные).
ИЕРАРХИЯ МОДЕЛЕЙ:
ЛОГИЧЕСКИЕ УРОВНИ МОДЕЛИРОВАНИЯ: ·
·
· X- входной сигнал F(X) - объект (модель - правило) Y –выходной сигнал
Методы решения.
ξ - СВ равномерно распределенная на [a,b]
Оценка интеграла J:
С(b-a) – общая площадь прямоугольника; оценка интеграла Q2:
Имеем две оценки:
Для того, чтобы уйти от усреднения, вводим
DQ – дисперсия оценки.
15. РЕГЕНЕРАТИВНЫЙ МЕТОД АНАЛИЗА МОДЕЛЕЙ Методы понижения дисперсии для имитационного моделирования: - Метод стратифицированной выборки (метод расслоения) - Регенеративный метод анализа модели
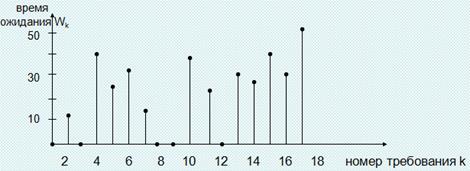
Примем за критерий качества функционирования системы E{W} – среднее время ожидания требованием (без учета времени обслуживания) в стационарном режиме.
Каждый цикл начинается при одних и тех же условиях и система в эти моменты «восстанавливается», группы данных последовательных циклов статистически независимы и имеют одинаковые распределения. Итак, если положить, например, Yk равной сумме значений длительностей ожидания на k-м цикле, а αk – числу требований, обслуженных на k-м цикле, то пары (Y1,α1), (Y2,α2), (Y3,α3), (Y4,α4) и (Y5,α5) – независимые и одинаково распределенные. Следовательно, сильно коррелированные данные {W1, W2….} разбились на статистически независимые и одинаково распределенные группы. Если N – общее число требований, обслуженных на n циклах, то
и E{W} = E{Y1}/E{α1}. Последовательность {Xn, n≥1} случайных векторов размерности K является регенерирующим процессом, если существует возрастающая последовательность 1≤β1<β2<…случайных дискретных моментов времени, называемых моментами регенерации, такая, что развитие процесса, начиная с каждого из этих моментов, определяется теми же вероятностными законами, что и в момент β1. Это значит, что между любыми двумя последовательными моментами регенерации, например βj и βj+1, часть процесса
{Xn, βj ≤ n < βj+1}
является независимой «вероятностной копией» части процесса между любыми двумя другими последовательными моментами регенерации. Однако для части процесса, заключенного между моментом 1 и моментом β1, хотя и независимой от остальных частей, допускается отличие от них по распределению. Часть процесса {Xn, βj ≤ n < βj+1} будем называть j-м циклом. Любой регенерирующий процесс с дискретным временем, представляющий практический интерес, имеет в некотором смысле стационарное распределение и наиболее часто в следующем привычном значении: существует К-мерный случайный вектор Х такой, что распределение Xn сходится к распределению X при n→∞, т.е.
24. МЕТОД СТРАТИФИЦИРОВАННОЙ ВЫБОРКИ Методы понижения дисперсии для имитационного моделирования: - Метод стратифицированной выборки (метод расслоения) - Регенеративный метод анализа модели Рассмотрение выборки может показать, есть ли сгущения. Пусть - μ величина среднего потребления некоторой группы населения. Необходимо оценить μ.
, где xi - потребление i-го выбранного индивидуума.
* - среднее значение для слоя,
* - количество индивидуумов в слое,
дисперсия оценки:
- оценивается с помощью S2:
Для заданной надежности (1-α) можно рассчитать доверительный интервал оценки μ: Zα/2 берем или из таблиц нормального распределения, или из распределения Стьюдента.
Если же сгущения большие, то:
Метод применим, когда есть явное сгущение данных. 11. МЕТОДОЛОГИЯ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ - это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте). ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. ИМИТАЦИОННАЯ МОДЕЛЬ — логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта. К имитационному моделированию прибегают, когда:
Имитационное моделирование, сохраняя основные приемы статистического моделирования, представляет собой современную технологию исследования сложных систем, использующую языковые и программные средства. ПРИМЕР ПРЕДСТАВЛЕНИЯ СМО В ВИДЕ АГРЕГАТА. АГРЕГАТ – это обобщенный объект, определяемый множествами T, X, Y, Z, B, g и операторами H и R, где: Оператор U:
ψ- длительность обслуживания,, где αj заменяется z3.
w//: время, когда заявка, l покидает систему необслуженной:
Операторы выхода
Z2y - если заявка уходит не обслуженной, y(t)=(y1,y2), где y1 - статус, y2 - содержание. y1 = 1, если обслуженная заявка покидает систему. y1 = 0, если заявка покидает систему не обслуженной.
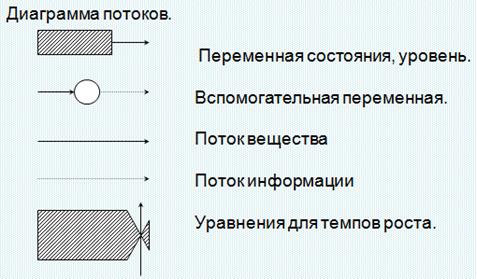
СИСТЕМНАЯ ДИНАМИКА СИСТЕМНАЯ ДИНАМИКА — направление в изучении сложных систем, исследующее их поведение во времени и в зависимости от структуры элементов системы и взаимодействия между ними. В том числе: причинно-следственных связей, петель обратных связей, задержек реакции, влияния среды и других. Особенное внимание уделяется компьютерному моделированию таких систем. Объект - организационно- экономические системы. Синергия - кооперативные действия: в экономической системе нельзя представить свойства единого целого как сумму свойств отдельных элементов системы. Синергия – это взаимодействие различных факторов, кооперативные действия которых выдают качественно новую характеристику системы – новое качество. Метод системной динамики позволяет анализировать объект в целом, так же имитационное моделирование позволяет исследовать динамику системы. В основе концепции системной динамики лежит представление о функционировании системы как совокупности потоков информации, энергии, промышленной продукции, денежных средств и т.п. Особенность метода системной динамики состоит в приближении программной реализации к виду, удобному для пользователя. Философия системной динамики базируется на предположении, что поведение (или история развития во времени) организации главным образом определяется ее информационно-логической структурой. Она отражает не только физические и технологические аспекты производственных процессов, но, что гораздо важнее, политику и традиции, которые явно или неявно определяют процесс принятия решений в организации. Методология системной динамики была построена так, чтобы сделать применимой на практике философию развития. Для этого были использованы и модифицированы известные методы представления потоковых диаграмм, математического и имитационного моделирования. На основе схем сигнальных потоков, применяемых для анализа электронных систем, были разработаны причинно-следственные диаграммы для визуального представления текущей ситуации. Как следующий шаг, для большинства системно-динамических проектов были созданы формальные потоковые диаграммы, представляемые в виде систем дифференциальных уравнений. Как потоковые диаграммы, так и системы уравнений выражают управленческие связи в помощью двух категорий: накопителей и потоков. Накопители представляют собой такие объекты реального мира, в которых сосредотачиваются некоторые ресурсы: знания (идеи), фонды, источники рабочей силы и т.п. Потоки – это все активные компоненты системы: потоки усилий (попыток), информационные потоки, расходные платежи и т.п. Если система управления представима в виде сети накопителей и потоков, то соответствующая системно-динамическая модель может быть реализована в виде компьютерной программы. С помощью такой программы можно провести экспериментальное тестирование предлагаемых изменений управленческой политики. Исследовательская группа из Mассачусетского технологического института разработала компилятор DYNAMO [1]. С помощью этого языка моделирования можно эффективно решать системы линейных и нелинейных алгебраических и дифференциальных уравнений, содержащих до нескольких тысяч переменных, при этом от пользователя не требуется глубоких знаний программирования. С появлением графических средств доступа язык моделирования DYNAMO, ранее более походивший на язык программирования высокого уровня, стал языком графического моделирования сложных динамических систем. Динамо (совокупность агрегированных операторов). В системе есть понятие «уровень», который меняется во времени, на выходе – «поток». Вся системная динамика сводится к двум моделям: модель потоков (динамика потоков), модель причинно-следственных связей (диаграмма причинно-следственных связей).
СВОЙСТВА СДВИГА БЕРНУЛЛИ. 1. Чувствительная зависимость итерации σ от начальных условий. Даже если две точки x и x/ отличаются друг от друга лишь в (n+1) знаке an+1, то под действием функции σ это различие увеличивается и их n -ые итерации σn(x) и σn(x/) будут отличаться уже в первом шаге. 2. У последовательности итераций σn(х0) сдвига Бернулли те же статические свойства, что и у последовательности подбрасывания монеты.
Зависимость порождается значением первой цифры после запятой, т.е. для σn(x0) это an+1. х0 = (0,10010…),
ХАРАКТЕРИСТИКИ ХАОТИЧЕСКОГО ДВИЖЕНИЯ Многоэтапные модели Рассматривается многоэтапная модель в предположении, что не учитывается стоимость размещения заказа. Кроме того, в модели предусматривается возможность задолженности и нулевое время поставки. Предполагается также, что спрос D в каждый период описывается стационарной (независящей от времени) плотностью вероятности f(D).
Метод Бокса-Уилсона. Метод Бокса — Уилсона простейший из методов планирования эксперимента. Однако его успешное применение зависит от решения многих вопросов, связанных с принятием неформализованных решений при выборе параметра оптимизации, факторов, плана экспериментов и при интерпретации результатов. (Верхний уровень обозначим «-»,Нижний – «+») «+»=Sio+λi «-»=Siо-λi Для S1: «+»=5,6 «-»=4,4; Для S2: «+»=5,2 «-»=3,8; Для S3: «+»=6,5 «-»=3,5; Для S4: «+»=125 «-»=75; Для S5: «+»=2,3 «-»=1,7; 2. Расчёт коэффициентов уравнения регрессии. -Свободный член уравнения: b0= -Коэффициент регрессии i-го фактора: bi= b1 = b4 = Корреляционные функции Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции. Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным. Свойства потоков 1. Стационарность. Означает независимость от времени вероятностных характеристик потока, т.е. вероятность попадания того или иного числа событий на участок времени длиной зависит только от длины участка и не зависит от того, где именно на оси Ot расположен этот участок. 2. Последействие. Введем два понятия – отсутствие последействия и ограниченность последействия. Отсутствие последействия – независимость числа событий, происходящих в непересекающиеся промежутки времени. Ограниченность последействия – независимость промежутков времени между наступлениями событий. Заметим, что обычно, если входной поток не имеет последействия, то выходной имеет последействие 3. Ординарность. Соответствует случаю, если вероятность попадания на элементарный участок Δt двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Имитация потока событий 1. Поток однородных событий ti - момент времени i-го события, т.е. требуется задать последовательность СВ t1,t2,…tm ξ1,ξ2…ξm – длины интервалов между событиями
Переходим к рассмотрению СВ ξ и пусть их совместная функция плотности f(z1,z2…zk)
Рассмотрим класс потоков с ограниченным последействием. Случайный поток однородных событий называется с ограниченным последействием, если СВ ξi независимы. Отсюда вытекает, что в этом случае совместная функция плотности f(z1,z2…zn)=f1(z1)*f2(z2)*…fn(zn). Функции fi(zi) при i>1 – условные функции плотности величин ξi при условии, что в начальный момент интервала ξi поступила заявка.
М – средняя длина интервала между последовательными заявками.
Формула Пальма связывает плотности f1(z1) и f(z)
Имитация векторных случайных величин
Cтандартный метод
частной (маргинальной) плотности распределения величины ξ1 и условных плотностей распределения ξк при условии, что ξ1=x1, ξ2=x2,… ξk-1=xk-1. Таким образом вектор ξ может моделироваться покомпонентно: сначала величина ξ1 с плотностью φ1(x) = f1(x1), далее ξ2 с φ2(x) = f2(x|ξ1) … последней ξm c φm(x)=fm(x|ξ1…ξm-1). Стандартный метод требует определенной вычислительной работы, связанной с нахождением условных и частных плотностей распределения компонент. После вычисления плотностей каждая компонента моделируется как скалярная величина известными методами.
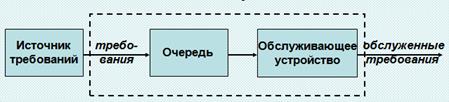
Производственные функции. ОСОБЕННОСТИ: · Иерархическая структура. · Наличие коллектива людей. · Многокритериальность. · Большой объем разнообразной информации (числовая, текстовая, символьная). · Неопределенность (по информации, по постановке задач, по критериям). · Трудности в подборе исходной информации, т.к. большое число скрытых внутренних закономерностей. · Высокий субъективный фактор. Аналитическим методом. Примеры: телефонные станции, ремонтные мастерские, билетные кассы и т.п. ОБЩАЯ ХАРАКТЕРИСТИКА: Каждая СМО состоит из какого-то числа обслуживающих единиц – КАНАЛОВ обслуживания (линии связи, рабочие точки). СМО могут быть одноканальными и многоканальными. СМО предназначена для обслуживания какого-то потока заявок, поступающих в общем случае в произвольные случайные промежутки времени. Обслуживание поступивших заявок продолжается какое-то время, после чего канал освобождается и снова готов к принятию заявок. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на вх. СМО скапливается излишне большое число заявок, в другие же периоды СМР будет работать с недогрузкой, либо вообще простаивать. Каждая СМО обладает какой-то пропускной способностью. В качестве характеристик эффективности могут выступать различные величины в зависимости от целей исследования. Предмет теории массового обслуживания – установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективностью обслуживания. Случайный характер потока заявок, а в общем случае, и длительности обслуживания, приводит к тому, что в СМО будет происходить какой-то случайный процесс. КЛАССИФИКАЦИЯ: 1) СМО с отказами; 2)СМО с очередями (*с неограниченным ожиданием, *с ограниченным ожиданием). Известна классификация, которая произведена, исходя из характеристик СМО. СМО классифицируют следующим образом. По потокам заявок СМО делятся на СМО с однородным потоком и приоритетные СМО. По дисциплинам обслуживания СМО делятся на СМО с дисциплиной FIFO (первый пришел – первый обслуживается), СМО с дисциплиной LIFO (последний пришел - первый обслуживается), СМО со случайным выбором на обслуживание. Моделирование систем с применением схем СМО предусматривает определение выходных параметров и параметров состояния, которые могут быть представлены как показатели эффективности СМО. Моделью, описывающей функционирование системы, может служить описание времени задержки в системе. В виде моделей могут быть применены коэффициент использования СМО, вероятность того, что поступившая в СМО заявка застанет ее свободной от обслуживания, описание периода занятости системы, вероятность отказа на обслуживание, среднее число заявок в очереди, описание выходных потоков заявок, интегральные характеристики функционирования СМО. Математическую модель СМО в виде системы уравнений Эрланга, как наиболее простую аналитическую модель, можно получить при пуассоновском потоке заявок и экспоненциальном распределении времени обслуживания. Удобство пользования данной моделью ограничивается требованием стационарности процессов и отсутствием необходимости оценки изменения вероятностных характеристик во времени. Если же перед исследователем ставится более слож
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 584; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.1.23 (0.012 с.) |



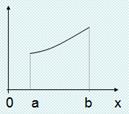 1) Вычисление среднего значения функции.
1) Вычисление среднего значения функции.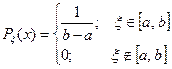
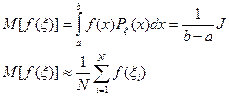
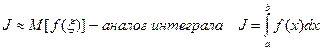

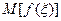 - оцениваемый параметр
- оцениваемый параметр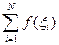 - оценка.
- оценка.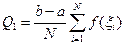
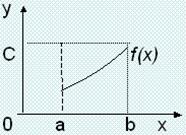 2) Метод геометрической интерпретации
2) Метод геометрической интерпретации 
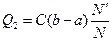
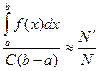
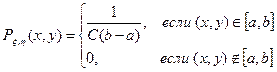 (ξ,η) двумерная точка с функцией плотности Рξ,η(х, у)
(ξ,η) двумерная точка с функцией плотности Рξ,η(х, у)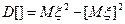
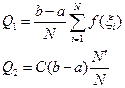
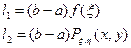 l – единичная реализация,
l – единичная реализация,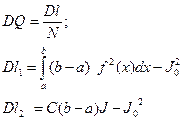
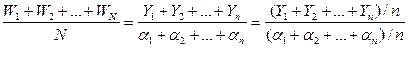
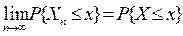
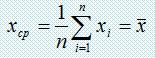
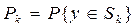 Для расслоения вводим стратифицирующую переменную yi – доход группы населения. Для получения yi необходимо отнести того или иного индивидуума к одному из k-слоев. Sk – слой из k-слоев (k=1,…,K). Пусть известна вероятность того, что индивидуум принадлежит k-слою:
Для расслоения вводим стратифицирующую переменную yi – доход группы населения. Для получения yi необходимо отнести того или иного индивидуума к одному из k-слоев. Sk – слой из k-слоев (k=1,…,K). Пусть известна вероятность того, что индивидуум принадлежит k-слою: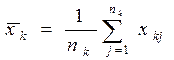
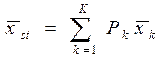 Тогда для оценки μ можно ввести стратифицирующую переменную
Тогда для оценки μ можно ввести стратифицирующую переменную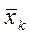
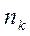
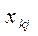
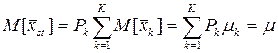 * - потребление j- индивидуума из k слоя.
* - потребление j- индивидуума из k слоя.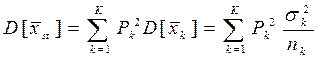 Оценка
Оценка 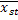 - несмещенная, т.к. математическое ожидание оценки:
- несмещенная, т.к. математическое ожидание оценки: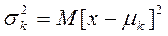
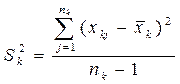
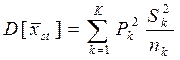 Следовательно, формула для практического счета дисперсии оценки выглядит следующим образом:
Следовательно, формула для практического счета дисперсии оценки выглядит следующим образом: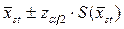
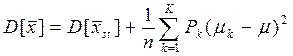 Дисперсия среднего арифметического, найденного без применения разделения на страты находится по следующей формуле:
Дисперсия среднего арифметического, найденного без применения разделения на страты находится по следующей формуле: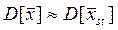
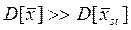 Таким образом, при малых сгущениях, т.е. когда μk и μ различаются мало, тогда
Таким образом, при малых сгущениях, т.е. когда μk и μ различаются мало, тогда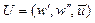
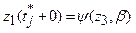
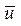 w/ - обслуживание очередной заявки окончено в момент времени;
w/ - обслуживание очередной заявки окончено в момент времени;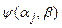 w/ - заявка покидает систему обслуживания:
w/ - заявка покидает систему обслуживания: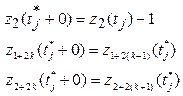
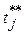
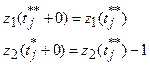
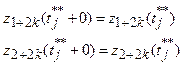 Для k<l:
Для k<l: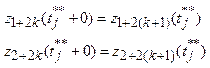 Для k>l:
Для k>l: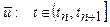 - оператор
- оператор 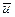 - это интервал между особыми состояниями. Особое состояние – это скачок в значении какой-л. переменной.
- это интервал между особыми состояниями. Особое состояние – это скачок в значении какой-л. переменной.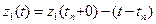 - время, оставшееся до конца обслуживания заявки.
- время, оставшееся до конца обслуживания заявки.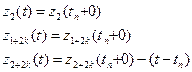
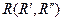
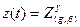
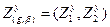 Z1y - если заявка уходит обслуженной,
Z1y - если заявка уходит обслуженной, 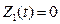
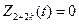
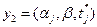 , где αj - параметр заявки, β - состояние системы, tj* - момент времени, в который ушла заявка.
, где αj - параметр заявки, β - состояние системы, tj* - момент времени, в который ушла заявка.
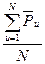 =
= 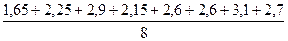 =
= 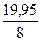 =2,49
=2,49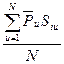
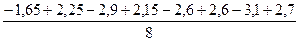 =-0.55; b2 =
=-0.55; b2 = 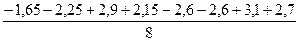 =1.75 b3 =
=1.75 b3 = 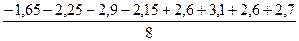 =2.05
=2.05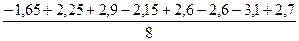 =0.95 b5 =
=0.95 b5 = 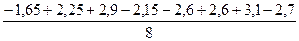 =1.75
=1.75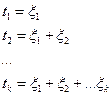
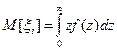
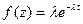
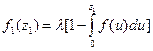 Допустим, что в стационарном потоке однородных заявок с ограниченным последействием имеет место равномерное распределение интервалов времени между заявками.
Допустим, что в стационарном потоке однородных заявок с ограниченным последействием имеет место равномерное распределение интервалов времени между заявками.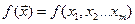 Рассмотрим моделирование непрерывной СВ ξ = (ξ1,ξ2…ξm). Ее полное описание задается совместной плотностью распределения
Рассмотрим моделирование непрерывной СВ ξ = (ξ1,ξ2…ξm). Ее полное описание задается совместной плотностью распределения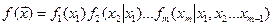 основан на представлении f(x) в виде произведения
основан на представлении f(x) в виде произведения


