
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип согласованного управленияСодержание книги
Поиск на нашем сайте
- это т. несогласованного оптимума.
Например: Центр планирует не только кол-во выпущенной продукции, но и затраты на производство.
Пусть wi – планируемые затраты i-го производства, которые определяются на основе оценок si, т.е. (wi = xi2/2si).
Конкретные запасы СУ получаются при выборе конкретных функций предпочтения для всех предприятий и процедуры выбора решения. Причем ХУ и ОУ – могут входить как частные случаи. Если обозначить αi(λ,xi,si) – некоторая функция предпочтения i-го предприятия, а ψ(x,s) – ц.ф. центра ψ(x,s)→min, ∑xi = R, xi ≥0 αi(xi,λ,si)= max z αi(λ,z,xi) Производственными функциями называют соотношения между используемыми в производстве материальными благами и трудовыми ресурсами к выпускаемой продукции. Q = f(K,L) Q – объем выпускаемой продукции (нац. доход) K – затраты капитала (фиксированные фонды, введенные в производство) L – объем трудовых затрат (производительно затраченное время) Использование ПФ предполагает решение двух взаимосвязанных задач: - спецификации ПФ, т.е. выделение существенных факторов и определение вида функции; - параметризации ПФ, т.е. расчета численных значений параметров на основе систематизированных статистических данных при помощи регрессионного и корреляционного анализа. ПФ могут быть построены в статическом (синхронном) аспекте на базе множества показателей для одного определенного момента (интервала) времени или в динамическом аспекте, на основе временных рядов. Спецификация ПФ должна удовлетворять некоторым логическим, экономическим и математическим требованиям: Оценку параметров ПФ часто производят МНК. Но статистические данные не вполне удовлетворяют требованиям МНК (например, корреляционная зависимость между факторами, тогда как способ НК требует их независимости). Поэтому применяются некоторые специальные приемы для устранения автокорреляции переменных и ослабления мультиколлениарности аргументов ПФ.
Показывает, сколько второго ресурса может быть высвобождено при увеличении затрат первого ресурса, если выпуск продукции остается неизменным.
Изокванты имеют отрицательный Сложная производственная функция сформулирована в 1930 г. Коббом и Дугласом. Они предположили, что нашли в ней наиболее адекватную форму выражения эффективности соотношения труда и основных фондов в образовании национального дохода. Известно, что α1+ α2 = 1 соответствует прирост производства пропорционален общему увеличению основных фондов к фонду заработной платы
|
|||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.74.47 (0.008 с.) |

 Согласованный оптимум означает преобразование конфликтной ситуации в такую, при которой ни один из участников конфликта не может улучшить свое состояние, не причинив вреда остальным партнерам (принцип Парето).
Согласованный оптимум означает преобразование конфликтной ситуации в такую, при которой ни один из участников конфликта не может улучшить свое состояние, не причинив вреда остальным партнерам (принцип Парето). Т. согласованного оптимума определяется Df/Dx, где D/Dx – якобиан, а f = (f1,…fn).
Т. согласованного оптимума определяется Df/Dx, где D/Dx – якобиан, а f = (f1,…fn).
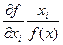
 При анализе эффективности использования ресурсов важно знать на сколько процентов возрастает объем продукции при увеличении затрат ресурса на 1%.
При анализе эффективности использования ресурсов важно знать на сколько процентов возрастает объем продукции при увеличении затрат ресурса на 1%. Предполагается, что ПФ удовлетворяет двум аксиомам.
Предполагается, что ПФ удовлетворяет двум аксиомам.


 ∂Q/∂K = QK> 0, QKK<0, ∂Q/∂L = QL> 0, QLL<0.
∂Q/∂K = QK> 0, QKK<0, ∂Q/∂L = QL> 0, QLL<0.


