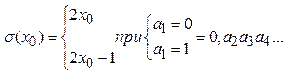Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод лемера и сдвиг бернулли. Детерминированный хаосСодержание книги
Поиск на нашем сайте
Первоначально слово хаос означало бесконечное пространство, существующее до появления всего остального. Позднее римляне интерпретировали хаос как изначальную сырую бесформенную массу, в которую Создатель привнес порядок и гармонию. В современном понимании хаос означает состояние беспорядка и нерегулярности. Будем рассматривать физические системы, поведение которых во времени детерминированно, т.е. существует правило в виде дифференциальных или разностных уравнений, определяющее их будущее исходя из заданных начальных условий. Всегда казалось, что детерминированное движение достаточно регулярно и далеко от хаотичности, поскольку последовательные состояния непрерывно развиваются одно из другого. Но еще на грани 19 и 20 веков А.Пуанкаре открыл, что в некоторых механических системах, эволюция которых определяется уравнениями Гамильтона, может появляться хаотическое движение. Все это воспринималось как курьез, пока в 1963 г. метеоролог Е.Н.Лоренц не обнаружил, что простая система из трех связанных нелинейных дифференциальных уравнений первого порядка может привести к совершенно хаотическим траекториям. Под детерминированным хаосом подразумевается нерегулярное или хаотическое движение, порожденное нелинейными системами, для которых динамические законы однозначно определяют эволюцию состояния системы во времени при известной предыстории. Нелинейность – необходимое, но не достаточное условие для возникновения хаотического движения. Хаос возникает не из-за внешних источников шума, не из-за бесконечного числа степеней свободы. Настоящая первопричина – свойство нелинейных систем экспоненциально быстро разводить первоначально близкие траектории в ограниченной области фазового пространства. Практически невозможно предсказать длительное поведение таких систем, поскольку реально начальные условия можно задать лишь с конечной точностью, а ошибки экспоненциально нарастают. Если пытаться решить такую нелинейную систему на ЭВМ, результат на все более дальних временах зависит от все большего количества цифр в числах, представляющих начальные условия. Так как цифры в иррациональных числах распределены нерегулярно, траектория становится хаотической. Рациональные числа – это положительные, отрицательные, 0, целые, дробные. Всякое рациональное число можно представить в виде m/n, где m и n – целые числа. Иррациональные числа так представить нельзя. π, е – иррациональные (трансцендентные) числа. Естественно возникают фундаментальные вопросы: 1. Можно ли по виду соответствующих дифференциальных уравнений предсказать наличие в системе детерминированного хаоса? 2. Можно ли более строго с точки математики определить понятие хаотического движения? 3. Означает ли существование детерминированного хаоса конец долговременно предсказуемости. СДВИГ БЕРНУЛЛИ.МЕТОД ЛЕМЕРА. Рассмотрим одномерное отображение:
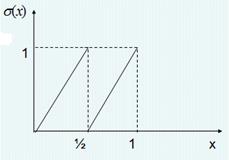
Это кусочно-линейное отображение, в котором наблюдается детерминированный хаос. При начальном значении х0 это отображение порождает последовательность итераций х0, х1=σ(х0), х2=σ(х1)…
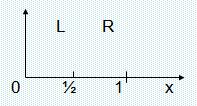
Тогда графическое представление преобразования σ(х) = 2х mod1: Первая итерация
Действие σ на двоичное представление х сводится к удалению первого знака после запятой и сдвигу оставшейся последовательности влево – это сдвиг Бернулли.
СВОЙСТВА СДВИГА БЕРНУЛЛИ. 1. Чувствительная зависимость итерации σ от начальных условий. Даже если две точки x и x/ отличаются друг от друга лишь в (n+1) знаке an+1, то под действием функции σ это различие увеличивается и их n -ые итерации σn(x) и σn(x/) будут отличаться уже в первом шаге. 2. У последовательности итераций σn(х0) сдвига Бернулли те же статические свойства, что и у последовательности подбрасывания монеты.
Зависимость порождается значением первой цифры после запятой, т.е. для σn(x0) это an+1. х0 = (0,10010…),
ХАРАКТЕРИСТИКИ ХАОТИЧЕСКОГО ДВИЖЕНИЯ
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.70.0 (0.005 с.) |

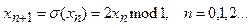
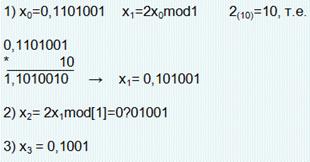
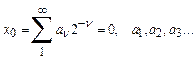
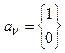
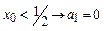 При:
При: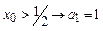
 :
: