
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этапы имитационного моделированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Формулировка проблемы. обоснование применения имитационного моделирования, определение целей. 2. Выявление существенных элементов системы, анализ взаимодействия элементов и внешних воздействий. 3. Формулировка математической модели. 4. Разработка алгоритмов и программирование имитационных моделей. 5. Оценка адекватности модели. Имитационное моделирование имеет особые трудности при решении проблемы адекватности модели, т.к. велик информационный фонд и сама модель – это совокупность большого количества моделей. *методы внешней оценки (эксперт оценивает входы, выходы, структуру, примерные результаты); *трассировка (анализируется логика моделирования); *внутренняя оценка (статистические критерии, типа критерия Фишера); *исторические подходы. 6. Планирование эксперимента При планировании эксперимента предполагается решение следующих проблем: *определение объема выборки; *большое число факторов; *многокомпонентная функция реализации. 7. Реализация машинных экспериментов в соответствии с выбранным планом. Особая роль отводится подготовке информации к диалоговой системе. 8. Обработка результатов экспериментов машинного и имитационного моделирования. Большая роль отводится методам понижения дисперсии.
29. МЕТОДЫ ПОНИЖЕНИЯ ДИСПЕРСИИ И МЕТОДЫ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
МЕТОДЫ ПОНИЖЕНИЯ ДИСПЕРСИИ ДЛЯИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ. Методы решения.
ξ - СВ равномерно распределенная на [a,b]
Оценка интеграла J:
С(b-a) – общая площадь прямоугольника; оценка интеграла Q2:
Имеем две оценки:
Для того, чтобы уйти от усреднения, вводим
DQ – дисперсия оценки.
15. РЕГЕНЕРАТИВНЫЙ МЕТОД АНАЛИЗА МОДЕЛЕЙ Методы понижения дисперсии для имитационного моделирования: - Метод стратифицированной выборки (метод расслоения) - Регенеративный метод анализа модели
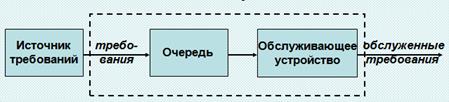
Примем за критерий качества функционирования системы E{W} – среднее время ожидания требованием (без учета времени обслуживания) в стационарном режиме.
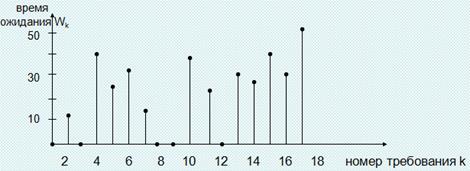
Каждый цикл начинается при одних и тех же условиях и система в эти моменты «восстанавливается», группы данных последовательных циклов статистически независимы и имеют одинаковые распределения. Итак, если положить, например, Yk равной сумме значений длительностей ожидания на k-м цикле, а αk – числу требований, обслуженных на k-м цикле, то пары (Y1,α1), (Y2,α2), (Y3,α3), (Y4,α4) и (Y5,α5) – независимые и одинаково распределенные. Следовательно, сильно коррелированные данные {W1, W2….} разбились на статистически независимые и одинаково распределенные группы. Если N – общее число требований, обслуженных на n циклах, то
и E{W} = E{Y1}/E{α1}. Последовательность {Xn, n≥1} случайных векторов размерности K является регенерирующим процессом, если существует возрастающая последовательность 1≤β1<β2<…случайных дискретных моментов времени, называемых моментами регенерации, такая, что развитие процесса, начиная с каждого из этих моментов, определяется теми же вероятностными законами, что и в момент β1. Это значит, что между любыми двумя последовательными моментами регенерации, например βj и βj+1, часть процесса
{Xn, βj ≤ n < βj+1}
является независимой «вероятностной копией» части процесса между любыми двумя другими последовательными моментами регенерации. Однако для части процесса, заключенного между моментом 1 и моментом β1, хотя и независимой от остальных частей, допускается отличие от них по распределению. Часть процесса {Xn, βj ≤ n < βj+1} будем называть j-м циклом. Любой регенерирующий процесс с дискретным временем, представляющий практический интерес, имеет в некотором смысле стационарное распределение и наиболее часто в следующем привычном значении: существует К-мерный случайный вектор Х такой, что распределение Xn сходится к распределению X при n→∞, т.е.
24. МЕТОД СТРАТИФИЦИРОВАННОЙ ВЫБОРКИ Методы понижения дисперсии для имитационного моделирования: - Метод стратифицированной выборки (метод расслоения) - Регенеративный метод анализа модели Рассмотрение выборки может показать, есть ли сгущения. Пусть - μ величина среднего потребления некоторой группы населения. Необходимо оценить μ.
, где xi - потребление i-го выбранного индивидуума.
* - среднее значение для слоя,
* - количество индивидуумов в слое,
дисперсия оценки:
- оценивается с помощью S2:
Для заданной надежности (1-α) можно рассчитать доверительный интервал оценки μ: Zα/2 берем или из таблиц нормального распределения, или из распределения Стьюдента.
Если же сгущения большие, то:
Метод применим, когда есть явное сгущение данных. 11. МЕТОДОЛОГИЯ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ - это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте). ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. ИМИТАЦИОННАЯ МОДЕЛЬ — логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта. К имитационному моделированию прибегают, когда:
Имитационное моделирование, сохраняя основные приемы статистического моделирования, представляет собой современную технологию исследования сложных систем, использующую языковые и программные средства.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.219 (0.006 с.) |

 СТРУКТУРА ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ.
СТРУКТУРА ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ. 
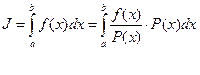

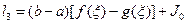
 МЕТОДЫ ПОНИЖЕНИЯ ДИСПЕРСИИ ДЛЯ МЕТОДА МОНТЕ-КАРЛО.
МЕТОДЫ ПОНИЖЕНИЯ ДИСПЕРСИИ ДЛЯ МЕТОДА МОНТЕ-КАРЛО.  l – единичная реализация
l – единичная реализация 3) Метод симметризации подынтегральной функции.
3) Метод симметризации подынтегральной функции.

 1) Вычисление среднего значения функции.
1) Вычисление среднего значения функции.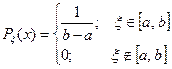
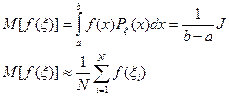
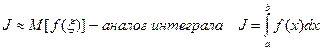

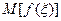 - оцениваемый параметр
- оцениваемый параметр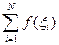 - оценка.
- оценка.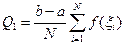
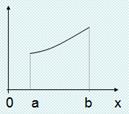
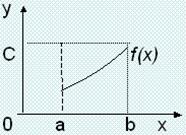 2) Метод геометрической интерпретации
2) Метод геометрической интерпретации 
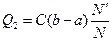
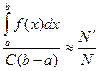
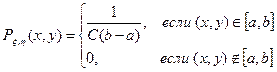 (ξ,η) двумерная точка с функцией плотности Рξ,η(х, у)
(ξ,η) двумерная точка с функцией плотности Рξ,η(х, у)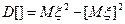
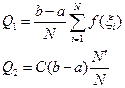
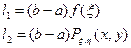 l – единичная реализация,
l – единичная реализация,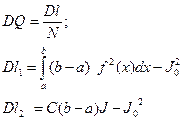
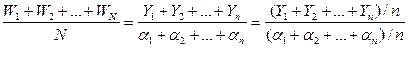
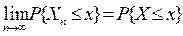
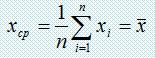
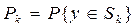 Для расслоения вводим стратифицирующую переменную yi – доход группы населения. Для получения yi необходимо отнести того или иного индивидуума к одному из k-слоев. Sk – слой из k-слоев (k=1,…,K). Пусть известна вероятность того, что индивидуум принадлежит k-слою:
Для расслоения вводим стратифицирующую переменную yi – доход группы населения. Для получения yi необходимо отнести того или иного индивидуума к одному из k-слоев. Sk – слой из k-слоев (k=1,…,K). Пусть известна вероятность того, что индивидуум принадлежит k-слою: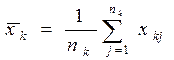
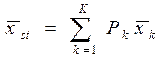 Тогда для оценки μ можно ввести стратифицирующую переменную
Тогда для оценки μ можно ввести стратифицирующую переменную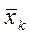
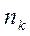
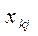
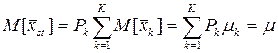 * - потребление j- индивидуума из k слоя.
* - потребление j- индивидуума из k слоя.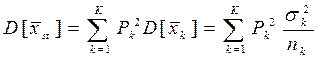 Оценка
Оценка 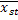 - несмещенная, т.к. математическое ожидание оценки:
- несмещенная, т.к. математическое ожидание оценки: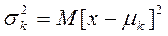
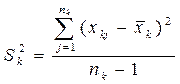
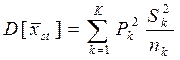 Следовательно, формула для практического счета дисперсии оценки выглядит следующим образом:
Следовательно, формула для практического счета дисперсии оценки выглядит следующим образом: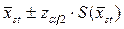
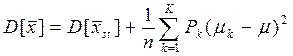 Дисперсия среднего арифметического, найденного без применения разделения на страты находится по следующей формуле:
Дисперсия среднего арифметического, найденного без применения разделения на страты находится по следующей формуле: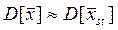
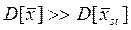 Таким образом, при малых сгущениях, т.е. когда μk и μ различаются мало, тогда
Таким образом, при малых сгущениях, т.е. когда μk и μ различаются мало, тогда


