
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы математической теории активных системСодержание книги
Поиск на нашем сайте
ЗАДАЧИ ПРОИЗВОДСТВА ПРОДУКЦИИ. Описание модели: Система состоит из планирующего органа – Центра и “n” предприятий - производителей однородной продукции – элементов. Исследуется функционирование системы в дискретные периоды (месяц, квартал, год) Задача центра – назначить план каждому предприятию при условии, чтобы суммарный выпуск продукции был равен заданному количеству R (плановое задание для системы в целом), а суммарные затраты на производство продукции были минимальными. xi - план «i»-го предприятия zi - затраты «i»-го предприятия на выпуск продукции в количестве xi. При заданном плане xi существует минимальная величина Зi(xi) затрат. Реальные затраты могут быть значительно выше этой величины (причины – плохая организация производства, отсутствие заинтересованности предприятия к снижению затрат). Так как затраты растут с ростом плана, то Зi(xi) – неубывающая функция xi. Для упрощения примем Задача центра - минимизировать затраты при выполнении планового задания
Задача предприятия
Формируем функцию:
μ – множитель Лагранжа. Дифференцируя по xi, получаем xi = μri:
оптимальный план:
Пусть λ = сonst. Для предприятия:
max (2-я производн. стр.)
А со стороны центра xi = siR/s Если xi(s*) < vi, то выгодная для предприятия оценка своих возможностей si*= D, т.к. xi(s) – возрастающая функция si. Если xi(s*)> vi, то si* = d. Если d<si*<D, то обязательно xi*=xi(s*)=vi. Нестрого, но видно, что при ∑vi>R и ∑vi<R решение при s*=D и s*=d - это x*=R/n.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.17.171 (0.007 с.) |

 Присутствие человека приводит к определенной активности системы. Активным называется элемент, имеющий собственные цели (интересы), способный искажать информацию и работать с разной эффективностью, в соответствии со своими интересами. ГЛАВНАЯ ЗАДАЧА, решаемая в теории активных систем – построение эффективных организационных механизмов (законов стимулирования, процедур планирования и др.)
Присутствие человека приводит к определенной активности системы. Активным называется элемент, имеющий собственные цели (интересы), способный искажать информацию и работать с разной эффективностью, в соответствии со своими интересами. ГЛАВНАЯ ЗАДАЧА, решаемая в теории активных систем – построение эффективных организационных механизмов (законов стимулирования, процедур планирования и др.)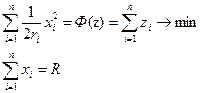
 а) Если бы центр знал коэффициент эффективности {ri} всех предприятий, то задача оптимального управления системой решается методом множителей Лагранжа.
а) Если бы центр знал коэффициент эффективности {ri} всех предприятий, то задача оптимального управления системой решается методом множителей Лагранжа.

 μ определяем из ∑ xi = R, т.е.
μ определяем из ∑ xi = R, т.е.
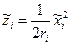 В этом случае центру достаточно назначить каждому “i” предприятию соответствующий план xi и обеспечить контроль за его выполнением. А предприятие заинтересовано реализовать план с минимальными затратами (fi = λxi – zi, т.к. λ и xi – фиксированы, тогда прибыль ↑).
В этом случае центру достаточно назначить каждому “i” предприятию соответствующий план xi и обеспечить контроль за его выполнением. А предприятие заинтересовано реализовать план с минимальными затратами (fi = λxi – zi, т.к. λ и xi – фиксированы, тогда прибыль ↑). Затраты на выпуск всей продукции будут при этом также минимальны
Затраты на выпуск всей продукции будут при этом также минимальны б) Проблемы возникают в том случае, если центр имеет ограниченную информацию о коэффициенте эффективности предприятий. Центру известны только границы возможных значений ri. Как центру принимать решение в этих условиях неопределенности?
б) Проблемы возникают в том случае, если центр имеет ограниченную информацию о коэффициенте эффективности предприятий. Центру известны только границы возможных значений ri. Как центру принимать решение в этих условиях неопределенности? т.е. прибыль предприятия зависит от оценок, сообщенных другими предприятиями. Игра «n» лиц с функциями выигрыша ρi(s), si – стратегия i-го игрока, [d,D] –множество возможных стратегий, S = {si}. Решение игры – ситуация равновесия в смысле Нэша, т.е.
т.е. прибыль предприятия зависит от оценок, сообщенных другими предприятиями. Игра «n» лиц с функциями выигрыша ρi(s), si – стратегия i-го игрока, [d,D] –множество возможных стратегий, S = {si}. Решение игры – ситуация равновесия в смысле Нэша, т.е.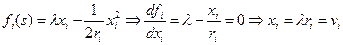 т.е. отдельному предприятию невыгодно менять стратегию, если остальные предприятия придерживаются прежних стратегий. План, выгодный предприятию:
т.е. отдельному предприятию невыгодно менять стратегию, если остальные предприятия придерживаются прежних стратегий. План, выгодный предприятию:


