
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование невырожденного многомерного нормального распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
µ = (µ1…µm)T – мат. ожидание ξ µ=Мξ R=[ρij] – заданная симметрич. положительно определенная матрица порядка «m»: (x-µ)TR-1(x-µ) квадратичная форма переменных y=x-µ с матрицей B=R-1 R=M(ξ-µ)(ξ-µ)T – корреляционная матрица вектора ξ B=R-1 – матрица точности. Распределение полностью описывается двумя параметрами вектором µ и матрицей R. Обозначим ξ ~ N(µ,R) Если м. о. равно нулю, а корреляционная матрица R равна единичной Im, т.е. ε~N(0,Im), то распределение называется стандартным нормальным распределением. Стандартное распределение легко моделируется. Для этого нужно положить все компоненты ξ равными независимым реализациям СВ ε ~ N(0,1). В общем случае многомерное нормальное распределение моделируется с помощью линейного преобразования ξ=Aε+µ ε ~ N(0,Im). Здесь матрица A=[aij] порядка «m» определяется условием R=A*AT (метод Холецкого) 8. АНАЛИЗ МЕТОДОВ ИМИТАЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ (ОДНОМЕРНЫЙ И МНОГОМЕРНЫЙ СЛУЧАИ)
2. ИМИТАЦИЯ РЕДКИХ СОБЫТИЙ Имитация случайных величин, подчиненныхзакону распределения Пуассона.
𝜆 – параметр распределения Если M[ ] = D[ ] = λ в заданном интервале с заданной точностью, то можно говорить, что это закон Пуассона. Распределение Пуассона является предельным для биномиального, когда (n→∞) и (p→∞) так, что np = 𝜆 = const Основное утверждение, на котором базируется имитация редких событий, гласит следующее:
1) P0(t) – вероятность того, что на интервале [0, t] не произойдет ни одного события.
12. ОЦЕНКА КОЛИЧЕСТВА РЕАЛИЗАЦИЙ, НЕОБХОДИМЫХ ДЛЯ ДОСТИЖЕНИЯ ТРЕБУЕМОЙ ТОЧНОСТИ В МЕТОДЕ СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ
Обозначим
Для уменьшения ε возможны два варианта:
5. МЕТОД МОНТЕ – КАРЛО И ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ - методология исследования и моделирования сложных систем – глобальное моделирование. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ - это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику. МЕТОД МОНТЕ-КАРЛО – метод решения математических задач с помощью моделирования случайных величин. МЕТОД МОНТЕ-КАРЛО - это численный метод, моделирующий на ЭВМ псевдослучайные числовые последовательности с заданными вероятностными характеристиками.
1) Универсальность 2) Простота реализации 3) Погрешность:
e - погрешность «-» медленная сходимость (сходимость по вероятности)
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.29 (0.007 с.) |

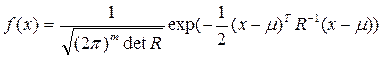 Случайный вектор ξ=(ξ1…ξm) имеет невырожденное m-мерное нормальное распределение, если его плотность распределения имеет вид
Случайный вектор ξ=(ξ1…ξm) имеет невырожденное m-мерное нормальное распределение, если его плотность распределения имеет вид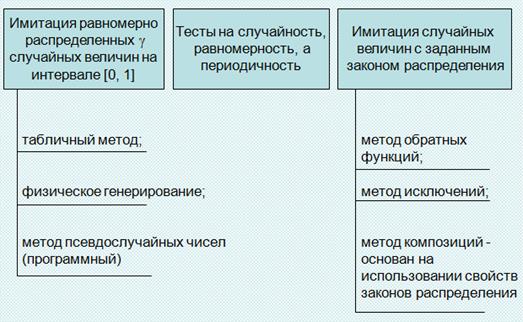 Имитация СВ с заданным законом распределения. Общая схема:
Имитация СВ с заданным законом распределения. Общая схема: Дискретная случайная величина х, принимающая целочисленные значения, распределена по закону Пуассона, если:
Дискретная случайная величина х, принимающая целочисленные значения, распределена по закону Пуассона, если: ---- > закон редких событий
---- > закон редких событий подчинено распределению Пуассона.
подчинено распределению Пуассона.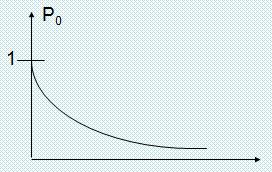
 P0(t+dt)= P0(t)(1- λdt)
P0(t+dt)= P0(t)(1- λdt) 2)
2) T – случайная величина, равная длине временного интервала между последовательными событиями.
T – случайная величина, равная длине временного интервала между последовательными событиями. Таким образом, для генерирования случайных величин, подчиненных з-ну Пуассона, сначала генерируются экспоненциально распределенные моменты {tij} наступления событий с м.о. I, которые потом суммируются до тех пор, пока итог не превысит
Таким образом, для генерирования случайных величин, подчиненных з-ну Пуассона, сначала генерируются экспоненциально распределенные моменты {tij} наступления событий с м.о. I, которые потом суммируются до тех пор, пока итог не превысит
 величину 𝜆.Как показал опыт, для большего быстродействия, можно применять следующее модифицированное выражение (λ=1 из экспоненциального закона)
величину 𝜆.Как показал опыт, для большего быстродействия, можно применять следующее модифицированное выражение (λ=1 из экспоненциального закона)



 - неравенство Чебышева (устанавливает верхнюю границу вероятности)
- неравенство Чебышева (устанавливает верхнюю границу вероятности) D[
D[  ] – дисперсия оценки а
] – дисперсия оценки а
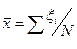
 Пусть ξ случайная величина с математическим ожиданием
Пусть ξ случайная величина с математическим ожиданием  :
: 

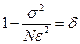

 При реализации метода Монте-Карло общее число реализаций велико, поэтому среднее арифметическое как СВ, подчиняется нормальному закону распределения с м.о. М[]=a и дисперсией D[]=σ2/N. В этом случае формула для погрешности принимает вид:
При реализации метода Монте-Карло общее число реализаций велико, поэтому среднее арифметическое как СВ, подчиняется нормальному закону распределения с м.о. М[]=a и дисперсией D[]=σ2/N. В этом случае формула для погрешности принимает вид: 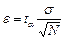 , где
, где 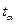 - находится из таблицы нормального распределения.
- находится из таблицы нормального распределения. ); *увеличить число реализаций (N)
); *увеличить число реализаций (N) ОСОБЕННОСТИ МЕТОДА МОНТЕ –КАРЛО:
ОСОБЕННОСТИ МЕТОДА МОНТЕ –КАРЛО:



