Модель с непрерывным контролем уровня запаса
Похожие статьи вашей тематики
Рассмотрим две модели управления запасами:
▪ обобщение детерминированной модели экономичного размера заказа на вероятностный случай, в которой используется буферный запас, отвечающий за случайный спрос;
▪ вероятностная модель экономичного размера заказа, учитывающая вероятностный характер спроса непосредственно в постановке задачи.
1.1 «Рандомизированная» модель эконом. размера заказа
Адаптируем детерминированную модель экономичного размера заказа для вероятностного спроса. Используем приближенный метод, который предполагает существование постоянного буферного запаса на протяжении всего планового периода. Размер резерва устанавливается так, чтобы вероятность истощения запаса в течение периода выполнения заказа (интервала между моментом размещения заказа и его поставкой) не превышала наперед заданной величины.
Введем следующие обозначения.
▪ L — срок выполнения заказа, т.е. время от момента размещения заказа до его поставки;
▪ X1— случайная величина, представляющая величину спроса на протяжении срока выполнения заказа;
▪ m1 — средняя величина спроса на протяжении срока выполнения заказа,
▪ σ1 — среднеквадратическое отклонение величины спроса на протяжении срока выполнения заказа;
▪ В — размер резервного запаса;
▪ α — максимально возможное значение вероятности истощения запаса на протяжении срока выполнения заказа.
Основным предположением при построении модели является то, что величина спроса Х1 на протяжении срока выполнения заказа L является нормально распределенной случайной величиной со средним μ1и стандартным отклонением σ1 т.е. имеет распределение N(μ1,σ1)
На рис. 1 показана зависимость между размером резервного запаса В и параметрами детерминированной модели экономичного размера заказа, которая включает срок выполнения заказа L, среднюю величину спроса μ1 а протяжении срока выполнения заказа и экономичный размер заказа у*. Заметим, что L должно быть равно эффективному времени выполнения заказа.
 Уровень запаса Уровень запаса
     Вероятностное условие, которое определяет размер резервного запаса В, имеет вид: Вероятностное условие, которое определяет размер резервного запаса В, имеет вид:
По определению случайная величина
является нормированной нормально распределенной случайной величиной, т.е. имеет распределение N(0, 1). Следовательно,
На рис. 2 показана величина, которая определяется из таблицы стандартного нормального распределения, так что
Следовательно, размер резервного запаса должен удовлетворять неравенству B≥σL.
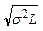 Величина спроса на протяжении срока выполнения заказа L обычно описывается плотностью распределения вероятностей, отнесенной к единице времени (например, к дню или неделе), из которой можно определить распределение спроса на протяжен периода L. В частности, если спрос за единицу времени является нормально распределенной случайной величиной со средним D и стандартным отклонением σ, то общий спрос на протяжении срока выполнения заказа L будет иметь распределение N(μL, σL), где μL=DL и σL=. Формула для σL получена на основании того, что значение L является целым числом (или же округлено до целого числа). Величина спроса на протяжении срока выполнения заказа L обычно описывается плотностью распределения вероятностей, отнесенной к единице времени (например, к дню или неделе), из которой можно определить распределение спроса на протяжен периода L. В частности, если спрос за единицу времени является нормально распределенной случайной величиной со средним D и стандартным отклонением σ, то общий спрос на протяжении срока выполнения заказа L будет иметь распределение N(μL, σL), где μL=DL и σL=. Формула для σL получена на основании того, что значение L является целым числом (или же округлено до целого числа).
1.2. Стохастический вариант модели экономичного размера заказа
"Рандомизированная" модель экономичного размера заказа не дает оптимальную политику управления запасами. Информация, имеющая отношение к вероятностной природе спроса первоначально не учитывается, а используется лишь независимо на последнем этапе вычислений. Рассмотрим более точную модель, в которой вероятностная природа спроса учитывается непосредственно в постановке задачи.
В новой модели допускается неудовлетворенный спрос (рис. 3). Заказ размером у размещается тогда, когда объем запаса достигает уровня R. Как и в детерминированном случае, уровень R, при котором снова размещается заказ, является функцией периода времени между размещением заказа и его выполнением. Оптимальные значения у и R определяются минимизацией ожидаемых затрат системы управления запасами, отнесенных к единице времени; они включают расходы на размещение заказа, на хранение, так и потери, связанные с неудовлетворенным спросом.

В рассматриваемой модели приняты три допущения.
1. Неудовлетворенный в течение срока выполнения заказа спрос накапливается.
2. Разрешается не более одного невыполненного заказа.
3. Распределение спроса в течение срока выполнения заказа является стационарным (неизменным) во времени.
Для определения функции, отражающей суммарные затраты, отнесенные к единице времени, введем следующие обозначения.
▪ f(x) — плотность распределения спроса х в течение срока выполнения заказа,
▪ D — ожидаемое значение спроса в единицу времени,
▪ h — удельные затраты на хранение (на единицу продукции за единицу времени),
▪ р — удельные потери от неудовлетворенного спроса (на единицу продукции за единицу времени),
▪ К — стоимость размещения заказа.
Основываясь на этих определениях, вычислим компоненты функции затрат.
1.  Стоимость размещения заказов. Приближенное число заказов в единицу времени равно D/y, так что стоимость размещения заказов в единицу времени равна KD/y. Стоимость размещения заказов. Приближенное число заказов в единицу времени равно D/y, так что стоимость размещения заказов в единицу времени равна KD/y.
2. Ожидаемые затраты на хранение. Средний уровень запаса равен
Следовательно, ожидаемые затраты на хранение за единицу времени равны hI.
Приведенная формула получена в результате усреднения ожидаемых запасов в начале и конце временного цикла, т.е. величин у + M{R-х} и M{R-х} соответственно. При этом игнорируется случай, когда величина R - М{х} может быть отрицательной, что является одним из упрощающих допущений рассматриваемой модели.
3. Ожидаемые потери, связанные с неудовлетворенным спросом.
2. Одноэтапные модели
Одноэтапные модели управления запасами отражают ситуацию, когда для удовлетворения спроса в течение определенного периода продукция заказывается только один раз. Например, модный сезонный товар устаревает к концу сезона, и, следовательно, заказы на него могут не возобновляться. В данном разделе рассматривается два типа таких моделей: с учетом и без учета затрат на оформление заказов.
При изложении данного материала используются следующие обозначения.
с — стоимость закупки (или производства) единицы продукции,
К — стоимость размещения заказа,
h — удельные затраты на хранение единицы продукции в течение рассматриваемого периода,
р — удельные потери от неудовлетворенного спроса (на единицу продукции за рассматриваемый период),
D — величина случайного спроса за рассматриваемый период,
f(D) — плотность вероятности спроса за рассматриваемый период,
у — объем заказа,
х — наличный запас продукта перед размещением заказа.
Модель определяет оптимальный объем заказа у, который минимизирует суммарные ожидаемые затраты, связанные с закупкой (или производством), хранением и неудовлетворенным спросом. При известном оптимальном значении у (обозначается у*) оптимальное управление запасами состоит в размещении заказа объемом у* - х, если х < y; в противном случае заказ не размещается.
2.1. Модель при отсутствии затрат на оформление заказа
В этой модели принято следующее.
1. Спрос удовлетворяется мгновенно в начале периода непосредственно после получения заказа.
2. Затраты на размещение заказа отсутствуют.
Рис. 4 иллюстрирует состояние запаса после удовлетворения спроса D. Если D<y, запас у—D хранится на протяжении периода. Если же D > у, возникает дефицит объема D — у.

2.2. Модель при наличии затрат на оформление заказа
Данная модель отличается от выше представленной тем, что учитывается стоимость К размещения заказа.
Многоэтапные модели
Рассматривается многоэтапная модель в предположении, что не учитывается стоимость размещения заказа. Кроме того, в модели предусматривается возможность задолженности и нулевое время поставки. Предполагается также, что спрос D в каждый период описывается стационарной (независящей от времени) плотностью вероятности f(D).
В многоэтапной модели учитывается приведенная стоимость денег. Если α (< 1) – коэффициент дисконтирования (процент скидки) для одного этапа, то сумма А спустя n этапов будет эквивалентна сумме α n А в настоящий момент.
Предположим, что горизонт планирования охватывает n этапов и неудовлетворенный спрос может оставаться таковым лишь на протяжении одного этапа. Пусть Fi(xi) — максимальная суммарная ожидаемая прибыль для этапов от i до n, определенная при условии, что хi — уровень имеющегося запаса перед размещением заказа на i-м этапе.
Метод Бокса-Уилсона.
Метод Бокса — Уилсона простейший из методов планирования эксперимента. Однако его успешное применение зависит от решения многих вопросов, связанных с принятием неформализованных решений при выборе параметра оптимизации, факторов, плана экспериментов и при интерпретации результатов.
При изложении материала были использованы элементы программированного обучения — «метод многовариантного ответа». Это сравнительно новый метод изложения, хотя тенденция к его распространению очевидна. Его цель — активизировать усвоение материала, выработать необходимые навыки.
1. Найдём физические значения верхнего и нижнего уровней факторов.
(Верхний уровень обозначим «-»,Нижний – «+»)
«+»=Sio+λi «-»=Siо-λi
Для S1: «+»=5,6 «-»=4,4; Для S2: «+»=5,2 «-»=3,8; Для S3: «+»=6,5 «-»=3,5;
Для S4: «+»=125 «-»=75; Для S5: «+»=2,3 «-»=1,7;
2. Расчёт коэффициентов уравнения регрессии.
-Свободный член уравнения: b0= 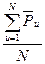 = = 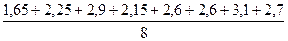 = = 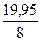 =2,49 =2,49
-Коэффициент регрессии i-го фактора: bi= 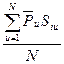
b1 = 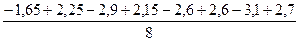 =-0.55; b2 = =-0.55; b2 = 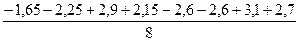 =1.75 b3 = =1.75 b3 = 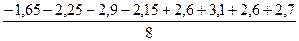 =2.05 =2.05
b4 = 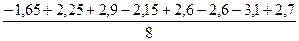 =0.95 b5 = =0.95 b5 = 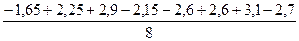 =1.75 =1.75
|




 Уровень запаса
Уровень запаса



 Вероятностное условие, которое определяет размер резервного запаса В, имеет вид:
Вероятностное условие, которое определяет размер резервного запаса В, имеет вид: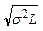 Величина спроса на протяжении срока выполнения заказа L обычно описывается плотностью распределения вероятностей, отнесенной к единице времени (например, к дню или неделе), из которой можно определить распределение спроса на протяжен периода L. В частности, если спрос за единицу времени является нормально распределенной случайной величиной со средним D и стандартным отклонением σ, то общий спрос на протяжении срока выполнения заказа L будет иметь распределение N(μL, σL), где μL=DL и σL=. Формула для σL получена на основании того, что значение L является целым числом (или же округлено до целого числа).
Величина спроса на протяжении срока выполнения заказа L обычно описывается плотностью распределения вероятностей, отнесенной к единице времени (например, к дню или неделе), из которой можно определить распределение спроса на протяжен периода L. В частности, если спрос за единицу времени является нормально распределенной случайной величиной со средним D и стандартным отклонением σ, то общий спрос на протяжении срока выполнения заказа L будет иметь распределение N(μL, σL), где μL=DL и σL=. Формула для σL получена на основании того, что значение L является целым числом (или же округлено до целого числа).
 Стоимость размещения заказов. Приближенное число заказов в единицу времени равно D/y, так что стоимость размещения заказов в единицу времени равна KD/y.
Стоимость размещения заказов. Приближенное число заказов в единицу времени равно D/y, так что стоимость размещения заказов в единицу времени равна KD/y.
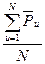 =
= 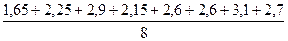 =
= 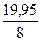 =2,49
=2,49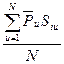
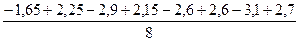 =-0.55; b2 =
=-0.55; b2 = 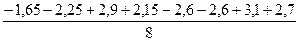 =1.75 b3 =
=1.75 b3 = 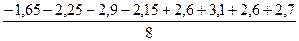 =2.05
=2.05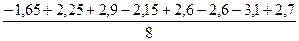 =0.95 b5 =
=0.95 b5 = 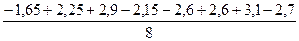 =1.75
=1.75


