
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы массового обслуживания; классификация и решение задачСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Аналитическим методом. Примеры: телефонные станции, ремонтные мастерские, билетные кассы и т.п. ОБЩАЯ ХАРАКТЕРИСТИКА: Каждая СМО состоит из какого-то числа обслуживающих единиц – КАНАЛОВ обслуживания (линии связи, рабочие точки). СМО могут быть одноканальными и многоканальными. СМО предназначена для обслуживания какого-то потока заявок, поступающих в общем случае в произвольные случайные промежутки времени. Обслуживание поступивших заявок продолжается какое-то время, после чего канал освобождается и снова готов к принятию заявок. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на вх. СМО скапливается излишне большое число заявок, в другие же периоды СМР будет работать с недогрузкой, либо вообще простаивать. Каждая СМО обладает какой-то пропускной способностью. В качестве характеристик эффективности могут выступать различные величины в зависимости от целей исследования. Предмет теории массового обслуживания – установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективностью обслуживания. Случайный характер потока заявок, а в общем случае, и длительности обслуживания, приводит к тому, что в СМО будет происходить какой-то случайный процесс. КЛАССИФИКАЦИЯ: 1) СМО с отказами; 2)СМО с очередями (*с неограниченным ожиданием, *с ограниченным ожиданием). Известна классификация, которая произведена, исходя из характеристик СМО. СМО классифицируют следующим образом. По потокам заявок СМО делятся на СМО с однородным потоком и приоритетные СМО. По дисциплинам обслуживания СМО делятся на СМО с дисциплиной FIFO (первый пришел – первый обслуживается), СМО с дисциплиной LIFO (последний пришел - первый обслуживается), СМО со случайным выбором на обслуживание. Моделирование систем с применением схем СМО предусматривает определение выходных параметров и параметров состояния, которые могут быть представлены как показатели эффективности СМО. Моделью, описывающей функционирование системы, может служить описание времени задержки в системе. В виде моделей могут быть применены коэффициент использования СМО, вероятность того, что поступившая в СМО заявка застанет ее свободной от обслуживания, описание периода занятости системы, вероятность отказа на обслуживание, среднее число заявок в очереди, описание выходных потоков заявок, интегральные характеристики функционирования СМО. Математическую модель СМО в виде системы уравнений Эрланга, как наиболее простую аналитическую модель, можно получить при пуассоновском потоке заявок и экспоненциальном распределении времени обслуживания. Удобство пользования данной моделью ограничивается требованием стационарности процессов и отсутствием необходимости оценки изменения вероятностных характеристик во времени. Если же перед исследователем ставится более сложная задача оценки таких критериев, как функции распределения вероятностей времени задержки, периода занятости, числа заявок в очереди. Наиболее широко применяется описание математических моделей в виде характеристических функций, в частности, в виде преобразований Лапласа-Стильтьеса. Модель времени задержки представима в виде интегро-дифференциального уравнения Линди-Такача-Севастьянова, причем в данной модели предполагается произвольный вид распределения времени обслуживания. Однако при всей универсальности аппарата характеристических функций для применения его при описании моделей СМО, у него имеется один существенный недостаток, заключающийся в том, что получить реальные распределения действительного параметра времени далеко не всегда возможно. Это связано с тем, что не всегда существуют обратные преобразования Лапласа. Если же рассматривать сложные структуры СМО (многофазные, многоканальные, приоритетные), то получить математическую модель в виде аналитических зависимостей невозможно. Поэтому для исследования сложных структур СМО разрабатывают имитационные модели. Аналитически решение задач теории МО сводится к составления систем дифференциальных уравнений Колмогорова. Методика построения имитационной модели СМО сложной структуры сводится к разработке модульной структуры алгоритмической модели. Структуру СМО необходимо декомпозировать на отдельные модули генерации заявок, распределения заявок при постановке в очередь и выбора из очереди, обслуживания заявок и набора статистических данных. При алгоритмизации СМО сложной структуры важно правильно выбрать последовательность обращений к подпрограммам в рассматриваемом такте моделирования. ОСНОВНЫЕ СООТНОШЕНИЯ СМО:
Распределение Пуассона
Где Pn(t) – вероятность того, что за промежуток t поступит n требований. СВОЙСТВА: е-λt - вероятность отсутствия требований в интервале t; λt(e-λt) - вероятность поступления одного требования за время t; Следовательно вероятность поступления за время t более одного требования:
т.е. функция, которая ведет себя как t2. Отсюда следует, что при малых t, все члены с t2 - пренебрежимо малы.
(1) - исходные выражения для пуассоновского распределения
*модель Эрланга (изменение Pn(t) в зависимости от t описывается Pn/(t), т.е. Pn/(t) = 0); * формула Поллачека- Хинчина (из рассмотрения, что также приводит к Pn(t), не зависящим от t.
Пусть случайная величина ξ принимает значения x1, x2, x3, x4, с вероятностями, соответственно, p1, p2, p3, p4. Требуется провести имитацию ξ. Для этого на отрезке [0, 1] обозначаем точки p1, p1 + p2, p1 + p2 + p3. Далее, после розыгрыша случайной равномерно распределенной величины γi, определим ее координату на отрезке [0—1]. Итак, если 0 ≤ γi, ≤ p1, то ξ принимает значение x1, то есть ξ = x1; если p1 ≤ γi, ≤ p1 + p2, то ξ = x2; если p1 + p2 ≤ γi, ≤ p1 + p2 + p3, то ξ = x3; если p1 + p2 + p3 ≤ γi, ≤ 1, то ξ = x4. Этот общий метод моделирования дискретной случайной величины основан на следующем соотношении:
где Случайная величина называется дискретной, если в результате испытания она может принимать значения из конечного либо счетного множества возможных числовых значений. 30.Задача определения давления в пласте с помощью метода Монте-Карло. Большое значение при разработке месторождений имеет задача определение давлений в нефтяном пласте. Для простоты ограничимся рассмотрением горизонтально расположенного нефтяного пласта. Бурение в пласте скважин вызывает приток жидкости к скважинам, т.е. имеет место перераспределение давления в пласте. Естественно, что технические решения разработки нефтяных и газовых пластов потребуют определения давления Задача может быть сформулирована следующим образом: отыскать внутри области функцию
и граничным условиям:
Здесь pi – давление на стенках пробуренных скважин; pk – давление в граничных узлах; k=k(x,y) – гидравлическая проводимость, отражающая основную характеристику поровой среды пласта. Заменим уравнение (19) системой конечно-разностных уравнений:
где p0 – искомое давление в узловой точке 0; p1, p2, p3, p4 – давление в соседних точках (в узлах 1, 2, 3, 4). Перепишем уравнения системы (21) следующим образом:
Здесь
Очевидно, что
Пусть требуется определить давление P0, то есть блуждания начинаются в точке 0. Правила перехода из начальной точки в соседнюю точку: 1. Моделируется равномерно распределенная в интервале [0,1] псевдослучайная величина. 2. Производится сравнение величины с коэффициентами Видно, что вероятность попадания в любой из окружающих узлов пропорциональна гидравлической проводимости пласта. Точно так же производятся последующие шаги – до попадания на границу скважины или области. После выхода на границу процесс блуждания снова повторяется. Отметим, что число испытаний N,будет определять точность вычислений. Если блуждающая точка n1 попала на граничную точку Pг1, ni - на граничную точку Pгi, nk – на граничную точку Pгк, то среднее значение функции p(x,y) в точке 0 подсчитывается по формуле
где N=n1+…+ni+…+nk.
|
||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 В теории МО обычно рассматривается один параметр – время. Базовый случайный процесс – пуассоновский.
В теории МО обычно рассматривается один параметр – время. Базовый случайный процесс – пуассоновский.
 При малых t вероятность наступления более одного требования пренебрежимо мала.
При малых t вероятность наступления более одного требования пренебрежимо мала.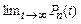 Рассмотрим стационарный режим. Понятие стационарного состояния классически поясняется в решении двух задач МО:
Рассмотрим стационарный режим. Понятие стационарного состояния классически поясняется в решении двух задач МО:



 ,
, , m = 0, 1, 2, …
, m = 0, 1, 2, … = Р(х, у).
= Р(х, у). (19)
(19) (20)
(20) (21)
(21) (22)
(22) (23)
(23)
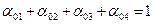 (24)
(24) : если
: если  , то блуждающая точка попадает в узел 1; если
, то блуждающая точка попадает в узел 1; если 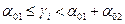 - в узел 2; если
- в узел 2; если  - в узел 3; если
- в узел 3; если 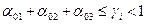 - в узел 4.
- в узел 4. (25)
(25)


