
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Имитация потоков событий и случайных векторных величин.Содержание книги
Поиск на нашем сайте
Общие характеристики потоков Поток событий – последовательность событий, происходящих одно за другим в какие-то моменты времени. Поток однородных событий – поток, события в котором различаются только моментами появления. Поток однородных случайных событий – случайный процесс с целочисленными неотрицательными значениями и непрерывным временем. Задается поток случайных событий двумя способами: • распределением числа событий, происходящих в интервале времени произвольной длины и расположенных произвольно относительно начала отсчета • распределением длительности интервалов между осуществлениями событий Поток событий регулярный, если события следуют одно за другим через строго определенные промежутки времени (предельный случай). Свойства потоков 1. Стационарность. Означает независимость от времени вероятностных характеристик потока, т.е. вероятность попадания того или иного числа событий на участок времени длиной зависит только от длины участка и не зависит от того, где именно на оси Ot расположен этот участок. 2. Последействие. Введем два понятия – отсутствие последействия и ограниченность последействия. Отсутствие последействия – независимость числа событий, происходящих в непересекающиеся промежутки времени. Ограниченность последействия – независимость промежутков времени между наступлениями событий. Заметим, что обычно, если входной поток не имеет последействия, то выходной имеет последействие 3. Ординарность. Соответствует случаю, если вероятность попадания на элементарный участок Δt двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Имитация потока событий 1. Поток однородных событий ti - момент времени i-го события, т.е. требуется задать последовательность СВ t1,t2,…tm ξ1,ξ2…ξm – длины интервалов между событиями
Переходим к рассмотрению СВ ξ и пусть их совместная функция плотности f(z1,z2…zk)
Рассмотрим класс потоков с ограниченным последействием. Случайный поток однородных событий называется с ограниченным последействием, если СВ ξi независимы. Отсюда вытекает, что в этом случае совместная функция плотности f(z1,z2…zn)=f1(z1)*f2(z2)*…fn(zn). Функции fi(zi) при i>1 – условные функции плотности величин ξi при условии, что в начальный момент интервала ξi поступила заявка.
М – средняя длина интервала между последовательными заявками.
Формула Пальма связывает плотности f1(z1) и f(z)
Имитация векторных случайных величин
Cтандартный метод
частной (маргинальной) плотности распределения величины ξ1 и условных плотностей распределения ξк при условии, что ξ1=x1, ξ2=x2,… ξk-1=xk-1. Таким образом вектор ξ может моделироваться покомпонентно: сначала величина ξ1 с плотностью φ1(x) = f1(x1), далее ξ2 с φ2(x) = f2(x|ξ1) … последней ξm c φm(x)=fm(x|ξ1…ξm-1). Стандартный метод требует определенной вычислительной работы, связанной с нахождением условных и частных плотностей распределения компонент. После вычисления плотностей каждая компонента моделируется как скалярная величина известными методами.
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.60.132 (0.009 с.) |

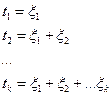
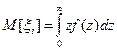
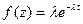
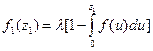 Допустим, что в стационарном потоке однородных заявок с ограниченным последействием имеет место равномерное распределение интервалов времени между заявками.
Допустим, что в стационарном потоке однородных заявок с ограниченным последействием имеет место равномерное распределение интервалов времени между заявками.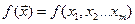 Рассмотрим моделирование непрерывной СВ ξ = (ξ1,ξ2…ξm). Ее полное описание задается совместной плотностью распределения
Рассмотрим моделирование непрерывной СВ ξ = (ξ1,ξ2…ξm). Ее полное описание задается совместной плотностью распределения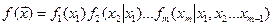 основан на представлении f(x) в виде произведения
основан на представлении f(x) в виде произведения


