
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение запаса для движения в направлении крутого восхождения
∆4 =150-100=50 ∆5 =3.5-2=1.5 4. Определение значимости коэффициентов регрессии. Найдём доверительный интервал N=8, t=2.31, Если (bi)> (b2 )=1,75>0.11 (b4) =0,95 >0.11 5. Расчёт критичности i-го фактора ( ( 6. Выбор шага крутого восхождения. обычно выбирают 5-8 шагов в направлении крутого восхождения пусть m=6 4-й фактор обладает минимальной критичностью
Проводим пошаговое приращение в каждом последующем опыте величины уровня фактора, учитывая знаки коэффициентов регрессии. b1 <0, проводим снижение величины уровня фактора на величину шага.
Классификация случайных процессов и корреляционные функции. Определение случайного процесса Теория случайных процессов – наука, изучающая закономерности случайных явлений и динамики их развития. Например: напряжение в сети, население в городе, броуновское движение, население города, запуск ракеты в космос и т.д. Случайной функцией называют функцию неслучайного аргумента t, которая при каждом фиксированном значении аргумента является случайной величиной. Случайные функции аргумента t обозначают прописными буквами X(t), Y(t) и т.д. Сечением случайного процесса называют случайную величину, соответствующую фиксированному значению в момент времени t = t0. Реализацией случайного процесса X(t) называют конкретный вид случайного процесса, который наблюдался на каком-то отрезке времени от 0 до τ Классификация случайных процессов Случайный процесс X(t) называется процессом дискретным во времени, если система в которой он протекает, меняет свои состояния только в моменты времени t1, t2,…,tn, число которых конечно или счетно.
1.а. дискретное время, дискретное состояние Корреляционные функции Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции. Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
|
|||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.123 (0.007 с.) |
 ,если bi>0 или
,если bi>0 или 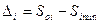 ∆1 =5-0=5 ∆2 =8.9-4.5=4.4 ∆3 =20-5=15
∆1 =5-0=5 ∆2 =8.9-4.5=4.4 ∆3 =20-5=15 =2;
=2; 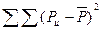 =2*0.16=0.32;
=2*0.16=0.32;  =2.31
=2.31  =2.31*0.496=0.11
=2.31*0.496=0.11 , то i-тый фактор значим (b1 )=0,55>0.11
, то i-тый фактор значим (b1 )=0,55>0.11 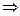 1-ый фактор значим
1-ый фактор значим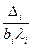 ) (
) ( )=
)=  =15,15
=15,15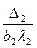 )=
)=  =3,59 (
=3,59 ( )=
)= 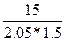 =4,88(
=4,88( )=
)=  =2,11 (
=2,11 ( )=
)=  =2,86
=2,86 =
= 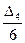 =50/6=8.33
=50/6=8.33 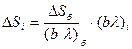
 =0.12
=0.12  =0.43
=0.43  =1.19
=1.19 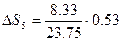 =0.18
=0.18


