
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие детерминированного хаоса и показатель Ляпунова.Содержание книги
Поиск на нашем сайте
хаос означает состояние беспорядка и нерегулярности. Будем рассматривать физические системы, поведение которых во времени детерминированно, т.е. существует правило в виде дифференциальных или разностных уравнений, определяющее их будущее исходя из заданных начальных условий. Под детерминированным хаосом подразумевается нерегулярное или хаотическое движение, порожденное нелинейными системами, для которых динамические законы однозначно определяют эволюцию состояния системы во времени при известной предыстории. Настоящая первопричина – свойство нелинейных систем экспоненциально быстро разводить первоначально близкие траектории в ограниченной области фазового пространства. Практически невозможно предсказать длительное поведение таких систем, поскольку реально начальные условия можно задать лишь с конечной точностью, а ошибки экспоненциально нарастают. Рациональные числа – это положительные, отрицательные, 0, целые, дробные. Всякое рациональное число можно представить в виде m/n, где m и n – целые числа. Иррациональные числа так представить нельзя. Показатель Ляпунова Под действием отображения соседние точки могут разбегаться, что ведет к хаотическому движению
В пределе при ε→0 и N→∞
λ(х0) – показатель Ляпунова определяет среднюю потерю информации о положении точки в [0,1] за одну итерацию.
Оценим потерю информации за одну итерацию.
Если длина интервала ↑, то n↓, I0 ↓. б) Линейное отображение f(x) изменяет длину интервала в a = │f /(0)│
Теперь сравним полученное выражение с формулой
Тогда
|
||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.110.45 (0.009 с.) |

 - показатель Ляпунова, характеризующий степень экспоненциального разбегания.
- показатель Ляпунова, характеризующий степень экспоненциального разбегания.
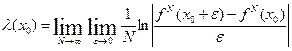
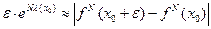 Cогласно определению показателя Ляпунова найдем λ(х0)
Cогласно определению показателя Ляпунова найдем λ(х0)
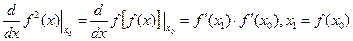 Термин «средняя потеря информации» появляется в связи с тем, что показатель Ляпунова характеризует хаотическое движение, т.е. отсутствие порядка, а информация непосредственно вычисляется на основе расчета энтропии.
Термин «средняя потеря информации» появляется в связи с тем, что показатель Ляпунова характеризует хаотическое движение, т.е. отсутствие порядка, а информация непосредственно вычисляется на основе расчета энтропии. а) Разобьем интервал [0,1] на n равных подинтервалов и предположим, что х0 может содержаться в каждом из них с вероятностью 1/n.
а) Разобьем интервал [0,1] на n равных подинтервалов и предположим, что х0 может содержаться в каждом из них с вероятностью 1/n.
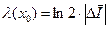

 Обобщение этого выражения, когда │f / (x)│ зависит от х, после усреднения по итерациям приводит к формуле для средней потери информации:
Обобщение этого выражения, когда │f / (x)│ зависит от х, после усреднения по итерациям приводит к формуле для средней потери информации:


