
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смо; классификация и решение задач с помощью имитационного моделированияСодержание книги
Поиск на нашем сайте
Примеры: телефонные станции, ремонтные мастерские, билетные кассы и т.п. ОБЩАЯ ХАРАКТЕРИСТИКА: Каждая СМО состоит из какого-то числа обслуживающих единиц – КАНАЛОВ обслуживания (линии связи, рабочие точки). СМО могут быть одноканальными и многоканальными. СМО предназначена для обслуживания какого-то потока заявок, поступающих в общем случае в произвольные случайные промежутки времени. Обслуживание поступивших заявок продолжается какое-то время, после чего канал освобождается и снова готов к принятию заявок. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на вх. СМО скапливается излишне большое число заявок, в другие же периоды СМР будет работать с недогрузкой, либо вообще простаивать. Каждая СМО обладает какой-то пропускной способностью. В качестве характеристик эффективности могут выступать различные величины в зависимости от целей исследования. Предмет теории массового обслуживания – установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективностью обслуживания. Случайный характер потока заявок, а в общем случае, и длительности обслуживания, приводит к тому, что в СМО будет происходить какой-то случайный процесс. КЛАССИФИКАЦИЯ: 1) СМО с отказами; 2)СМО с очередями (*с неограниченным ожиданием, *с ограниченным ожиданием). Известна классификация, которая произведена, исходя из характеристик СМО. СМО классифицируют следующим образом. По потокам заявок СМО делятся на СМО с однородным потоком и приоритетные СМО. По дисциплинам обслуживания СМО делятся на СМО с дисциплиной FIFO (первый пришел – первый обслуживается), СМО с дисциплиной LIFO (последний пришел - первый обслуживается), СМО со случайным выбором на обслуживание. Моделирование систем с применением схем СМО предусматривает определение выходных параметров и параметров состояния, которые могут быть представлены как показатели эффективности СМО. Моделью, описывающей функционирование системы, может служить описание времени задержки в системе. В виде моделей могут быть применены коэффициент использования СМО, вероятность того, что поступившая в СМО заявка застанет ее свободной от обслуживания, описание периода занятости системы, вероятность отказа на обслуживание, среднее число заявок в очереди, описание выходных потоков заявок, интегральные характеристики функционирования СМО. Математическую модель СМО в виде системы уравнений Эрланга, как наиболее простую аналитическую модель, можно получить при пуассоновском потоке заявок и экспоненциальном распределении времени обслуживания. Удобство пользования данной моделью ограничивается требованием стационарности процессов и отсутствием необходимости оценки изменения вероятностных характеристик во времени. Если же перед исследователем ставится более сложная задача оценки таких критериев, как функции распределения вероятностей времени задержки, периода занятости, числа заявок в очереди. Наиболее широко применяется описание математических моделей в виде характеристических функций, в частности, в виде преобразований Лапласа-Стильтьеса. Модель времени задержки представима в виде интегро-дифференциального уравнения Линди-Такача-Севастьянова, причем в данной модели предполагается произвольный вид распределения времени обслуживания. Однако при всей универсальности аппарата характеристических функций для применения его при описании моделей СМО, у него имеется один существенный недостаток, заключающийся в том, что получить реальные распределения действительного параметра времени далеко не всегда возможно. Это связано с тем, что не всегда существуют обратные преобразования Лапласа. Если же рассматривать сложные структуры СМО (многофазные, многоканальные, приоритетные), то получить математическую модель в виде аналитических зависимостей невозможно. Поэтому для исследования сложных структур СМО разрабатывают имитационные модели. Аналитически решение задач теории МО сводится к составления систем дифференциальных уравнений Колмогорова. Методика построения имитационной модели СМО сложной структуры сводится к разработке модульной структуры алгоритмической модели. Структуру СМО необходимо декомпозировать на отдельные модули генерации заявок, распределения заявок при постановке в очередь и выбора из очереди, обслуживания заявок и набора статистических данных. При алгоритмизации СМО сложной структуры важно правильно выбрать последовательность обращений к подпрограммам в рассматриваемом такте моделирования. ОСНОВНЫЕ СООТНОШЕНИЯ СМО: В теории МО обычно рассматривается один параметр – время. Базовый случайный процесс – пуассоновский.
Где Pn(t) – вероятность того, что за промежуток t поступит n требований. СВОЙСТВА: е-λt - вероятность отсутствия требований в интервале t; λt(e-λt) - вероятность поступления одного требования за время t; Следовательно вероятность поступления за время t более одного требования:
т.е. функция, которая ведет себя как t2. Отсюда следует, что при малых t, все члены с t2 - пренебрежимо малы.
(1) - исходные выражения для пуассоновского распределения
*модель Эрланга (изменение Pn(t) в зависимости от t описывается Pn/(t), т.е. Pn/(t) = 0); * формула Поллачека- Хинчина (из рассмотрения, что также приводит к Pn(t), не зависящим от t.
|
||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.119.34 (0.006 с.) |

 Распределение Пуассона
Распределение Пуассона
 При малых t вероятность наступления более одного требования пренебрежимо мала.
При малых t вероятность наступления более одного требования пренебрежимо мала.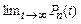 Рассмотрим стационарный режим. Понятие стационарного состояния классически поясняется в решении двух задач МО:
Рассмотрим стационарный режим. Понятие стационарного состояния классически поясняется в решении двух задач МО:








