
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однопродуктивна статична модельСодержание книги
Поиск на нашем сайте
Модель управління запасами простого типу характеризується сталим у часі попитом, миттєвим збільшенням запасу і відсутністю дефіциту. На рис. 23.1 показано зміну рівня запасу з часом. Припускається, що інтенсивність попиту (в одиницю часу) дорівнює
Рис. 23.2. Зміна рівня запасу з часом в однопродуктовій статичній моделі
Найвищого рівня запас досягає в момент постачання замовлення розміром у (припускається, що запізнення постачання є заданою константою). Рівень запасу досягає нуля протягом у/ Чим менший розмір замовлення у, тим частіше потрібно розміщувати нові замовлення. Однак при цьому середній рівень запасу буде зменшуватися. З іншого боку, зі збільшенням розміру замовлень рівень запасу збільшується, але замовлення розміщуються рідше (рис. 2.3). Так як витрати залежать від частоти розміщення замовлення й об’єму запасу, що зберігається, то величина у обирається згідно з умовою забезпечення оптимального балансу між двома видами витрат. Це лежить в основі побудови відповідної моделі управління запасами. Нехай К – витрати на оформлення замовлення, що мають місце щоразу при його розміщенні в припущенні, що витрати на зберігання одиниці замовлення в одиницю часу рівні h. Отже, сумарні витрати в одиницю часу С(у) як функцію від у можна представити у вигляді (23.3): С (у) =
Рисунок. 2.3. Зміна рівня запасу з часом в залежності від частоти розміщення замовлень
Тривалість циклу руху замовлення складає:
і середній рівень запасу становить у / 2. Оптимальне значення у отримується в результаті мінімізації С(у) по у. Таким чином, у припущенні, що у* неперервна змінна, одержуємо:
звідки оптимальне значення розміру замовлення визначається виразом:
Оскільки друга похідна в точці у* строго додатна, досягається мінімум. Отриманий вираз для розміру замовлення, зазвичай, називають формулою економічного розміру замовлення Уілсона. Оптимальна стратегія моделі передбачає замовлення у* через кожні t0*=у * /
L L Рис. 2.4. Функціонування системи з запізненням Для більшості реальних ситуацій існує (позитивний) термін виконання замовлення (тимчасове запізнення) L від моменту розміщення замовлення до його дійсної поставки. Стратегія розміщення замовлень у наведеній моделі повинна визначати точку відновлення замовлення. Рис. 2.4. ілюструє випадок, коли точка відновлення замовлення повинна випереджати на L одиниць часу очікуване надходження. У практичних цілях цю інформацію можна просто перетворювати, визначивши точку відновлення замовленнячерез рівень запасу, який відповідає моменту відновлення замовлення. На практиці це реалізується шляхом неперервного контролю рівня запасу до моменту досягнення чергової точки відновлення замовлення. Можливо, з цієї причини модель економічного розміру замовлення деколи називають моделлю неперервного контролю стану замовлення. Потрібно відзначити, що з точки зору аналізу в умовах стабілізації системи термін виконання замовлення L можна завжди прийняти меншим за тривалість циклу t*0. Прийняті в розглянутій вище моделі припущення можуть не відповідати деяким реальним умовам внаслідок вірогіднішого характеру попиту. На практиці отримав розповсюдження наближений метод, який зберігає простоту моделі економічного розміру замовлення і в той же час у якійсь мірі враховує вірогідніший характер попиту. Ідея методу надзвичайно проста. Вона передбачає створення деякого (постійного) буферного запасу на всьому горизонті планування. Розмір резерву визначається таким чином, щоб вірогідність зменшення запасу протягом періоду виконання замовлення L не перевищувала наперед заданої величини. Припустимо, що f(r) – щільність розподілу вірогідності попиту протягом цього терміну. Надалі припустимо, що вірогідність зменшення запасу протягом періоду L не повинна перевищувати а.Тоді розмір резервного запасу В визначиться з умови P (r>B+Lß)<a, де L ß є споживання протягом часу L. Немає причин припускати, що загальний результат використання процедур визначення В й економічного розміру замовлення обов’язково оптимальний або близький до оптимального. Відхилення від оптимуму пояснюється тим, що на початку деяка суттєва інформація не враховується, а потім використовується зовсім неявно на останньому етапі обчислень. По суті, витрати на зберігання резерву В можна розглядати просто як деяку «ціну» за те, що вся наявна інформація у процесі аналізу одночасно не використовується.
Різновиди моделей економічного розміру замовлення (партії) припускають можливість дефіциту і рівномірного (а не миттєвого) збільшення запасу. Останній випадок є типовим для виробничих систем, в яких інтенсивність збільшення є функцією інтенсивності виробництва. В цих ситуаціях у моделях управління запасами, як і раніше, співставляються витрати на зберігання запасів і оформлення замовлень. В функцію сумарних витрат включаються також втрати від дефіциту, якщо він має місце. В загальному випадку втрати від дефіциту припускаються пропорційними середній величині дефіциту. 24. [16 с.34-38 ]
Однопродуктова статична модель з«розривами» цін В попередніх моделях не враховуються окремі витрати на придбання товарів, так як вони сталі і не впливають на рівень запасу. Однак в багатьох випадках ціна одиниці продукції залежить від розмірів закупленої партії. У таких випадках ціни змінюються стрибкоподібно або надаються гуртові знижки. При цьому в моделі управління запасами необхідно враховувати витрати на придбання. Розглянемо модель управління запасами з миттєвим збільшенням запасу за відсутності дефіциту. Припустимо, що ціна одиниці продукції дорівнює с1, при у<q і рівна с2, при у>q, де с1>с2 і q – розмір замовлення, при перевищенні якого надається знижка. Тоді сумарні витрати за цикл, незважаючи на затримки в оформленні замовлення і зберігання запасу, повинні включати затримки придбання. Сумарні витрати в одиницю часупри у<q становлять:
а при у>q ці витрати становлять:
Графіки цих двох функцій наведені на рис. 2.5. Нехтуючи впливом зниження цін, позначимо через у т розмір замовлення, при якому досягається мінімум величин С 1 і С2.
C 1
C2
Рис. 24.1. Графіки сумарних витрат в одиницю часу Звигляду функцій витрат С1 і С2 робимо висновок, що оптимальний розмір замовлення у* залежить від того, де саме стосовно трьох показаних на рисунку зон І, II і III знаходиться точка розриву ціни q. Ці зони знаходяться наступним чином: Зона І: 0 Наведене графічне розв’язання рівняння для розглянутого випадку, яке залежить від того, де знаходиться qвідносно зон І, ІІ і ІІІ (рис. 2.6). В результаті оптимальний розмір замовлення у визначається наступним чином:
Алгоритм визначення у * має наступні основні кроки: Крок 1. Визначити ут = Крок 2. Визначити q 1 з рівняння C1(yт)=C(q1) і встановити, де саме відносно зон II і Ш знаходиться значення q. а) Якщо ут б) Якщо q
С1
С2
q ym q1 Рис. 2.6. Модель з розривами цін
У будь-якій задачі управління запасами вирішується питання вибору розмірів і термінів розміщення замовлень на продукцію. На жаль, спільне рішення цих завданнь неможливо одержати на основі однієї моделі. Тому розроблені найрізноманітніші моделі, що описують різні окремі випадки. Одним з вирішальних факторів при розробці моделі управління запасами є характер попиту. У найбільш простих моделях передбачається, що попит є статичним детермінованим.
Ми проаналізували такі моделі управління запасами: модель Уілсона без обмежень та з обмеженнями на складські приміщення, однопродуктову статичну модель, однопродуктова статичну модель з «розривами» цін. У більшості розглянутих моделей управління запасами здійснюється оптимізація функції витрат, що включає витрати на оформлення замовлень, закупівлю і зберігання продукції, а також втрати від дефіциту. Втрати від дефіциту зазвичай найбільш складно оцінити, тому вони можуть бути обумовлені такими нематеріальними факторами, як, наприклад, погіршення репутації. З іншого боку, хоч оцінку витрат на оформлення замовлення отримати неважко, включення в модель цієї статті витрат істотно ускладнює математичний опис завдання. Відомі моделі управління запасами рідко точно описують реальну систему. Тому рішення, що отримується на основі моделей цього класу, слід розглядати скоріше як принципові висновки, а не конкретні рекомендації. 25. [17, с. 3-5]
Модель планирования экономичного размера партии
Модель Уилсона, используемую для моделирования процессов закупки продукции у внешнего поставщика, можно модифицировать и применять в случае собственного производства продукции. На рис. 11.3 схематично представлен некоторый производственный процесс. На первом станке производится партия деталей с интенсивностью λ деталей в единицу времени, которые используются на втором станке с интенсивностью ν [дет./ед.t].
Рис. 11.3. Схема производственного процесса
Входные параметры модели планирования экономичного размера партии 1) λ – интенсивность производства продукции первым станком, [ед. тов./ед. t]; 2) ν – интенсивность потребления запаса, [ед. тов./ед. t]; 3) s – затраты на хранение запаса, [руб./ ед.тов.⋅ ед.t ]; 4) K – затраты на осуществление заказа, включающие подготовку (переналадку) первого станка для производства продукции, потребляемой на втором станке, [руб.]; 5) tп – время подготовки производства (переналадки), [ед.t]. Выходные параметры модели планирования экономичного размера партии 1) Q – размер заказа, [ед. тов.]; 2) L – общие затраты на управление запасами в единицу времени, [руб./ед.t]; 3) τ – период запуска в производство партии заказа, т.е. время между включениями в работу первого станка, [ед. t];
4) h0 – точка заказа, т.е. размер запаса, при котором надо подавать заказ на производство очередной партии, [ед. тов.]. Изменение уровня запасов происходит следующим образом (рис. 11.4): - в течение времени t1 работают оба станка, т.е. продукция производится и потребляется одновременно, вследствие чего запаса накапливается с интенсивностью (λ − ν); - в течение времени t2 работает только второй станок, потребляя накопившийся запас с интенсивностью ν.
Рис. 11.4. График циклов изменения запасов в модели планирования экономичного размера партии
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.212.51 (0.012 с.) |

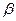 .
.


 одиниць часу після отримання замовлення розміром у.
одиниць часу після отримання замовлення розміром у.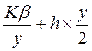 . (23.3)
. (23.3)


 ,
, .
. (рис. 2.4).
(рис. 2.4).

 ,
, .
.







 Тоді у т =
Тоді у т =  .
.
 q < у т ; Зона II: у т
q < у т ; Зона II: у т  q 1.
q 1.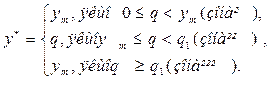
 , якщо q < ут, то q знаходиться взоні І, тоді у*= ут. В іншому випадку перейти до кроку 2.
, якщо q < ут, то q знаходиться взоні І, тоді у*= ут. В іншому випадку перейти до кроку 2.








