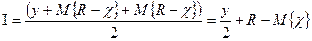Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класифікація економіко математичних моделей управління запасамиСодержание книги
Поиск на нашем сайте Колективний звіт за результатами індивідуальної навчально-дослідної роботи на тему: «Огляд і аспекти класифікації економіко-математичних моделей управління запасами» з дисципліни «Економіко-математичні моделі в управлінні та економіці»
Виконавець студенти групи ОА-111 Митько А.П. Міщенко А.М.
Консультант Виконали студенти, а хто така ця Ющенко, яке вона мала право їх консультувати???? Ющенко Н.Л.
Чернігів ЧДТУ 2013
Класифікація економіко математичних моделей управління запасами
1 Класифікація економіко-математичних моделей задач управління запасами за цільовим призначенням (класифікаційна ознака взята з джерела [№ 21 у списку, с. 19-20]): 1.1 Теоретико-аналітичні: Що означає такий запис тут і далі? Яким стандартом користувались? 11[c.16-20], 23. [16, с. 30-34], 24. [16 с.34-38 ], 26. [18, с. 175-180], 1.2 Прикладні: 1[c.141-146],2[c.10-13], 3[c.56-62],4[c.127-140], 5[c.328-377], 6[c.38-43], 7[c.76-88], 8[c.22-35], 9[c.32-38], 10[c.37-42], 12[c.25-29], 13[c.208-215], 14. [14, с.14-15], 15. [14, с.15-17], 16. [14, с. 21-23], 17. [14, с. 23-24], 18. [15, с.10-17], 19. [16, с.13-16], 20. [16, с. 20-22], 21. [16 c.22-26], 22. [16 c.23-26], 25. [17, с. 3-5], 27. [19, с. 45-46], 28. [19, с.46-48], 29. [20, с. 7-10], 30. [20, с. 11-13] 2 Класифікація економіко-математичних моделей задач управління запасами у залежності від способу відображення (класифікаційна ознака взята з джерела [№ 21 у списку, с.19-20]): 2.1 Дискретні: 1[c.141-146], 2[c.10-13], 4[c.127-140], 6[c.38-43], 9[c.32-38], 11[c.16-20], 12[c.25-29], 19. [16, с.13-16], 22. [16 c.23-26], 2.2 Неперервні: 3[c.56-62], 7[c.76-88], 8[c.22-35], 10[c.37-42], 13[c.208-215], 15. [14, с.15-17], 21. [16 c.22-26], 24. [16 с.34-38 ], 30. [20, с. 11-13] 2.3 Змішані: 5[c.328-377], 16. [14, с. 21-23], 18. [15, с.10-17], 23. [16, с. 30-34], 25. [17, с. 3-5], 29. [20, с. 7-10], 3 Класифікація економіко-математичних моделей задач управління запасами за масштабом економічного об’єкту (класифікаційна ознака взята з джерела [№ 21 у списку, с. 19-20]): 3.1 Макроекономічні: ?????? 3.2 Мезомоделі: ?????? 3.3 Мікроекономічні: 1[c.141-146], 2[c.10-13], 3[c.56-62], 4[c.127-140], 5[c.328-377], 6[c.38-43], 7[c.76-88], 8[c.22-35], 9[c.32-38], 10[c.37-42], 11[c.16-20], 12[c.25-29], 13[c.208-215], 14. [14, с.14-15], 15. [14, с.15-17], 16. [14, с. 21-23], 18. [15, с.10-17], 19. [16, с.13-16], 20. [16, с. 20-22], 21. [16 c.22-26], 22. [16 c.23-26], 23. [16, с. 30-34], 24. [16 с.34-38 ], 25. [17, с. 3-5], 26. [18, с. 175-180], 27. [19, с. 45-46], 28. [19, с.46-48], 29. [20, с. 7-10], 30. [20, с. 11-13]
4.Класифікація економіко-математичних моделей задач управління запасами за характером кінцевої мети (класифікаційна ознака взята з джерела [№ 21 у списку, с. 19-20]): 4.1 Описові: 14. [14, с.14-15], 22. [16 c.23-26], 24. [16 с.34-38 ],27. [19, с. 45-46], 28. [19, с.46-48], 4.2 Оптимізаційні: 1[c.141-146], 2[c.10-13], 3[c.56-62], 4[c.127-140], 5[c.328-377], 6[c.38-43], 7[c.76-88], 8[c.22-35], 9[c.32-38], 10[c.37-42], 11[c.16-20], 12[c.25-29], 13[c.208-215], 15. [14, с.15-17], 17. [14, с. 23-24], 18. [15, с.10-17], 19. [16, с.13-16], 20. [16, с. 20-22], 21. [16 c.22-26], 22. [16 c.23-26], 23. [16, с. 30-34], 25. [17, с. 3-5], 29. [20, с. 7-10], 30. [20, с. 11-13]
5. Класифікація економіко-математичних моделей задач управління запасами у залежності від рівня формалізованості зв’язків між ними (класифікаційна ознака взята з джерела [№ 21 у списку, с.19-20 ]): 5.1 Алгоритмічні: 1[c.141-146], 3[c.56-62], 4[c.127-140], 5[c.328-377], 6[c.38-43], 7[c.76-88], 8[c.22-35], 9[c.32-38], 10[c.37-42], 11[c.16-20], 12[c.25-29], 13[c.208-215], 14. [14, с.14-15], 16. [14, с. 21-23], 17. [14, с. 23-24], 18. [15, с.10-17], 19. [16, с.13-16], 20. [16, с. 20-22], 21. [16 c.22-26], 22. [16 c.23-26], 23. [16, с. 30-34], 25. [17, с. 3-5], 26. [18, с. 175-180], 27. [19, с. 45-46], 28. [19, с.46-48], 29. [20, с. 7-10], 30. [20, с. 11-13] 5.2 Аналітичні: 2[c.10-13], 15. [14, с.15-17], 24. [16 с.34-38 ], 6 Класифікація економіко-математичних моделей задач управління запасами залежності від впливу випадкових та невизначених факторів (класифікаційна ознака взята з джерела [№ 21 у списку, с.19-20 ]): 6.1 Детерміновані: 4[c.127-140], 9[c.32-38], 11[c.16-20], 12[c.25-29], 14. [14, с.14-15], 16. [14, с. 21-23], 18. [15, с.10-17], 23. [16, с. 30-34], 24. [16 с.34-38 ], А їх поділ, наприклад, за Саковичем В.А. «Исследование операций: справочное пособие», 1985 г., с. 211–249? 6.2 Моделі з невизначеними факторами: - 6.3 Стохастичні: 1[c.141-146], 2[c.10-13], 3[c.56-62], 5[c.328-377], 6[c.38-43], 7[c.76-88], 8[c.22-35], 10[c.37-42], 13[c.208-215], 15. [14, с.15-17], 17. [14, с. 23-24], 19. [16, с.13-16], 20. [16, с. 20-22], 21. [16 c.22-26], 26. [18, с. 175-180], 27. [19, с. 45-46], 28. [19, с.46-48], 29. [20, с. 7-10], 30. [20, с. 11-13] 7 Класифікація економіко-математичних моделей задач управління запасами За зміною в часі (класифікаційна ознака взята з джерела [№ 21 у списку, с.19-20 ]): 7.1 Статичні: 3[c.56-62], 4[c.127-140], 5[c.328-377], 6[c.38-43], 7[c.76-88], 8[c.22-35], 10[c.37-42], 11[c.16-20], 12[c.25-29], 13[c.208-215], 14. [14, с.14-15], 15. [14, с.15-17], 16. [14, с. 21-23], 20. [16, с. 20-22], 21. [16 c.22-26], 22. [16 c.23-26], 23. [16, с. 30-34], 24. [16 с.34-38 ], 27. [19, с. 45-46], 28. [19, с.46-48], 29. [20, с. 7-10], 30. [20, с. 11-13] 7.2 Динамічні: 1[c.141-146], 2[c.10-13], 18. [15, с.10-17], 19. [16, с.13-16], 25. [17, с. 3-5], 29. [20, с. 7-10], 8. Співвідношення між ендогенними і екзогенними змінними моделей задач управління запасами (класифікаційна ознака взята з джерела [№ 22 у списку, с. 34-35 ]): 8.1 А чому далі, наприклад, при поділі за 10 ознакою, з малої букви йде? Відкриті: 1[c.141-146], 2[c.10-13], 3[c.56-62], 4[c.127-140], 5[c.328-377], 6[c.38-43], 7[c.76-88], 8[c.22-35], 9[c.32-38], 10[c.37-42], 11[c.16-20], 12[c.25-29], 13[c.208-215], 15. [14, с.15-17], 17. [14, с. 23-24], 18. [15, с.10-17], 19. [16, с.13-16], 20. [16, с. 20-22], 22. [16 c.23-26], 23. [16, с. 30-34], 24. [16 с.34-38 ], 28. [19, с.46-48], 29. [20, с. 7-10], 8.2 Закриті: 14. [14, с.14-15], 16. [14, с. 21-23], 18. [15, с.10-17], 26. [18, с. 175-180], 9. Номенклатура продукції моделей задач управління запасами (класифікаційна ознака взята з джерела [№ 22 у списку, с. 34-35]):: 9.1 Одно продуктові: 1[c.141-146], 4[c.127-140], 6[c.38-43], 7[c.76-88], 8[c.22-35], 9[c.32-38], 10[c.37-42], 11[c.16-20], 12[c.25-29], 14. [14, с.14-15], 15. [14, с.15-17], 16. [14, с. 21-23], 21. [16 c.22-26], 22. [16 c.23-26], 23. [16, с. 30-34], 24. [16 с.34-38 ],
Навіть у рекомендованому мною на лекції навч. посібнику можна відшукати однопродуктові економіко–математичні моделі: Без дефіциту 9.1.1.1 попит неперервний (уілсона) Урахування дискретності попиту Моделі зі скінченною інтенсивністю надходження партії товару При дефіциті Коли незадоволені вимоги ставляться на облік Моделі з утратою незадоволених потреб В умовах знижкина розмір замовлення Оптова знижка Диференційована знижка і т.д. стосовно цього й інших типів моделей....
9.2 Багатопродуктові: 2[c.10-13], 3[c.56-62], 5[c.328-377], 13[c.208-215], 17. [14, с. 23-24], 18. [15, с.10-17], 22. [16 c.23-26], 25. [17, с. 3-5], 27. [19, с. 45-46], 29. [20, с. 7-10], 10. За ступенем ймовірності моделей задач управління запасами (класифікаційна ознака взята з джерела [№ 22 у списку, с. 34-35]): 10.1 аналітичні: 1[c.141-146], 3[c.56-62], 4[c.127-140], 5[c.328-377], 6[c.38-43], 7[c.76-88], 8[c.22-35], 9[c.32-38], 11[c.16-20], 12[c.25-29], 13[c.208-215], 14. [14, с.14-15], 15. [14, с.15-17], 16. [14, с. 21-23], 17. [14, с. 23-24], 19. [16, с.13-16], 20. [16, с. 20-22], 21. [16 c.22-26], 22. [16 c.23-26], 23. [16, с. 30-34], 24. [16 с.34-38 ], 25. [17, с. 3-5], 27. [19, с. 45-46], 28. [19, с.46-48], 10.2 економетричні: 18. [15, с.10-17], 10.3 змішані: 2[c.10-13], 26. [18, с. 175-180],29. [20, с. 7-10], 30. [20, с. 11-13]. 11. За точністю математичного відображення моделей задач управління запасами (класифікаційна ознака взята з джерела [№ 22 у списку, с. 34-35]): 11.1 Лінійні: 1[c.141-146], 2[c.10-13], 3[c.56-62], 4[c.127-140], 5[c.328-377], 10[c.37-42], 11[c.16-20], 12[c.25-29], 13[c.208-215], 9[c.32-38], 14. [14, с.14-15], 15. [14, с.15-17], 16. [14, с. 21-23], 17. [14, с. 23-24], 18. [15, с.10-17], 19. [16, с.13-16], 20. [16, с. 20-22], 21. [16 c.22-26], 22. [16 c.23-26], 23. [16, с. 30-34], 24. [16 с.34-38 ], 25. [17, с. 3-5], 27. [19, с. 45-46], 28. [19, с.46-48], 29. [20, с. 7-10], 30. [20, с. 11-13]; 11.2Нелінійні: 6[c.38-43], 7[c.76-88], 8[c.22-35], 26. [18, с. 175-180]. 12 Період управління моделей задач управління запасами (класифікаційна ознака взята з джерела [№ 22 у списку, с.34-35 ]): 12.1Довгострокові: 2[c.10-13], 3[c.56-62], 4[c.127-140], 7[c.76-88], 13[c.208-215], 25. [17, с. 3-5], 29. [20, с. 7-10]; 12.2 Короткострокові: 18. [15, с.10-17], 19. [16, с.13-16]; 12.3 Поточні: 1[c.141-146], 5[c.328-377], 6[c.38-43], 8[c.22-35], 9[c.32-38], 10[c.37-42], 11[c.16-20], 12[c.25-29], 14. [14, с.14-15], 15. [14, с.15-17], 16. [14, с. 21-23], 17. [14, с. 23-24], 20. [16, с. 20-22], 21. [16 c.22-26], 22. [16 c.23-26], 23. [16, с. 30-34], 24. [16 с.34-38 ], 26. [18, с. 175-180], 27. [19, с. 45-46], 28. [19, с.46-48], 30. [20, с. 11-13].
УВАГА! Основним недоліком цієї класифікації, крім того що вона містить дуже багато повторень одних і тих же економіко–математичних моделей (суттєвий «–«) та не претендує на повну (це нормально і слід зауважити про це у звіті), є те, що Ви у каталозі наводите різноманітні моделі, наприклад, під №18, взятими з [15, с.10-17] містяться як оптимізаційні так і економетричні моделі. А, отже, доцільно уточнювати (з посиланням на конкретні формули) які економіко–математичні моделі відносяться до одного типу, а які до іншого!!! Тим більше мені не зрозуміло чому ви з одного й того ж перешоджерела одні моделі виокремили, а інші ні (наприклад, з [14] Вами виділені моделі під №№14–17 у каталозі (додаток А), з [16] – моделі №№19–24.
Додатки
Додаток А Каталог підібраних економіко-математичних моделей упраління запасами
Домбровский В.В., Чаусова Е.В. Математическая модель управления запасами при случайном сезонном спросе и ненадежных поставщиках / Домбровский В.В., Чаусова Е.В. // Вестник томского государственного университета. 2000. − № 271. − С. 141-146 Проблема управління запасами є однією з найбільш важливих в організаційному управлінні. Але, як правило, не існує типових рішень - умови на кожному підприємстві або фірмі унікальні і включають безліч обмежень і різних особливостей. З цим пов'язані і проблеми, що виникають при розробці математичної моделі та визначенні оптимальної стратегії управління запасами. У даній роботі на прикладі фірми, яка займається доставкою кам'яного вугілля в райони Томської області, будується модель управління запасами вугілля і здійснюється пошук оптимальної стратегіі поведінки, яка гарантує фірмі отримання найбільшого прибутку, враховуючи всі особливості її споживачів, постачальників і ринку, на якому вона працює. У розділі 1 досліджується структура формування запасів розглянутої фірми, що дозволяє встановити характер даної системи управління запасами. Продовження додатку А
У розділі 2 наводиться загальна схема побудови оптимізаційної моделі для знаходження оптимальної стратегії управління запасами з точки зору отримання мінімуму загальних очікуваних витрат за весь період планування запасів і досягнення бажаного рівня обслуговування споживачів. При цьому враховується існуючий ряд обмежень на обсяги оформлюваних замовлень, які пов'язані з можливостями і надійністю постачальників, специфікою транспортування вантажу, пропускною здатністю річкового порту та об'ємом майданчики, орендованій у річкового порту, для зберігання вугілля. У розділі 3 проводиться аналіз рішення, отриманого засобом моделі, описаної в розділі 2. Досліджуючи побудовані оптимальні стратегії управління запасами для різних рівнів запасу на початок періоду планування, вдається виявити ряд закономірностей щодо отримано результату поточного рівня запасів на складі і сполученого з ним рівня обслуговування споживачів.
1. Структура формування запасів на фірмі Фірма повинна розробити календарну програму формування запасів вугілля на майбутній період планування. В якості критерію оптимальності управління, тобто вибору розміру замовлення, використовуються повні очікувані витрати протягом всього періоду планування. Перерахуємо особливості структури управління запасами на фірмі. 1. Фірма здійснює періодичний контроль за рівнем запасів і щомісяця поповнює свої запаси, оформляючи заявку на поставку вугілля, розмір якої залежить від рівня запасів на початок поточного місяця, передбачуваної величини сумарного попиту до кінця періоду планування та очікуваної величини поставки. 2. Величина реального попиту стає відомою тільки після оформлення замовлення на поставку вугілля. Цей попит по можливості задовольняється за рахунок створених запасів, при дефіциті незадоволений попит відкладається і задовольняється за рахунок наступних поставок. Фірма має декілька постійних джерел поповнення запасів. При плануванні замовлень перед підприємствам-постачальникам необхідно враховувати реальні можливості і надійність кожного постачальника. Керуючись накопиченим досвідом, бажано робити замовлення більше, ніж імовірно вимагається вугілля насправді, так як велика ймовірність того, що хтось з постачальників зірве угоду. До того ж завжди може з'явитися «несподіваний клієнт», який не зробив запасів вугілля на зиму. 4. Поставки по кожному замовленню, незалежно від підприємства-постачальника, здійснюються на протязі місяці за попередньою домовленістю про терміни поставки з кожним постачальником. 5. Вартість однієї тонни вугілля не залежить від підприємства-постачальника і включає в себе транспортні витрати, пов'язані з перевезенням вантажу по залізниці. Вартість одного вагона вугілля розраховується з припущення його повної загрузки, тобто фірмі невигідно оформляти замовлення на неповний вагон, тому що це автоматично збільшує вартість одиниці вугілля. 6. Роблячи замовлення на поставку вугілля, фірма повинна враховувати пропускну спроможність залізниці дороги, обсяг майданчика в річковому порту, яка орендується фірмою для зберігання вугілля, і добову спроможність річкового порту до прийняття вантажу, так як в разі несвоєчасної розвантаження вагонів фірма платить залізниці досить великий штраф за простій вагонів. Мета фірми - розробити стратегію управління запасами, при якій мінімізується загальна сума очікуваних витрат, пов'язаних з надходженням вугілля в річковій порт, змертвінням капіталу в запасах і штрафом за відкладений попит, а попит задовольняється із прийнятим рівнем обслуговування споживачів.
2. Побудова математичної моделі оптимального управління запасами 2.1. Побудова цільової функції для перетворення якісного опису моделі в математичну модель введемо позначення: іt - Рівень запасу на початок відрізка t, який може приймати негативні значення за наявності відкладеного попиту; yt- нестаціонарна від’ємна дискретна випадкова величина, характери
Так як обсяг поставки випадковий і залежить від розміра поданого замовлення конкретного постачальника, введемо вектор невід'ємних дискретних випадкових величин вектор поставок, де випадкова величина поставки в період t k-м постачальником і описується умовним розподілом Тоді стан запасу вугілля на складі можна описати стохастичним різницевим рівнянням:
Передбачається, що випадкові величини незалежні і стаціонарні. Оскільки в розглянутому випадку попит є нестаціонарним, з яскраво вираженими сезонними коливаннями і, взагалі кажучи, залежним, будемо будувати стратегію управління на основі прогнозних значень попиту Відомо, що будь поставка, незалежно від підприємств-постачальників, має дворівневу структуру і здійснюється за принципом: "все (з ймовірністю p) або нічого (з ймовірністю 1-p) ", тоді структура умовного розподілу випадкової величини
де ймовірність p (k) характеризує надійність k-го постачальника. Нехай випадкові величини
Зауваження: тут випадкові величини позначені прописними літерами, а прийняті ними значення - малими. Такі позначення будуть використовуватися протягом всієї роботи. В якості цільової функції візьмемо суму очікуваних на кожному відрізку планування витрат усіх видів. Нехай b - витрати, пов'язані з виконанням замовлення; h - показник, пов'язаний із заморожуванням грошових коштів, вкладених в одну тонну вугілля; із - штраф за нестачу одиниці продукту протягом одного проміжку часу між двома послідовними кроками, (b, h, c - постійні протягом усього періоду планування). Нехай всі витрати визначаються станом системи в кінці чергового тимчасового проміжку. Тоді очікувані витрати, пов'язані з надходженням вугілля на склад, зберіганням запасів і штрафними втратами у разі відкладеного попиту, на відрізку t при початковому рівні запасів i і векторі замовлень
де випадкового вектора Хt при векторі замовлень
Тоді
У прийнятих позначеннях цільова функція має вигляд
2.2. Побудова допустимої області Розглянемо обмеження на вектор замовлень Для побудови допустимої області замовлень введемо ряд позначень. Нехай W - об'єм складу; V – ємність залізничного вагона; Pt-пропускна здатність порту в період t; ω - бажаний рівень обслуговування (відношення задоволеного попиту до пред’явленого). Задамо можливості постачальників вектором Згідно перерахованим вище характерним особливостей системи управління запасами фірми, область допустимих рішень можна представити як
і задача (2) зводиться до знаходження на кожному кроці планування запасів невід’ємного цілочисельного вектора і має наступний вигляд:
Простору Q і Іt представлені формулами (3), (4).
,
де
причому якщо
де
Назвемо поведінкою набір функцій
визначальних для вектора замовлень, який необхідно сформувати на t-му кроці, якщо наявний рівень запасів дорівнює i. Кожному поведінки буде відповідати певне математичне сподівання сумарних витрат для процесу планування замовлень. Оптимальна лінія поведінки
повинна задовольняти умові мінімуму повних очікуваних витрат за весь період планування:
де іt відомий до початку процесу планування запасів, а іt визначається рекурентним співвідношенням:
2.3. Визначення оптимальної стратегії Введемо послідовність функцій
Використовуючи перетворення (1), отримуємо:
де
a
Особливістю побудованої моделі є безперервність змінної i, що характеризує поточний рівень запасів вугілля в річковому порту. Це випливає з прямої залежності рівня запасів від величини пред'явленого попиту, яка може приймати не тільки дискретні значення. У цьому випадку неможливо безпосередньо знайти значення функції Зауваження. Область Qt, По якій шукається мінімум 3. Перевірка моделі і аналіз результатів моделювання Аналіз продажів вугілля за три роки показав, що попит на вугілля має явно виражений сезонний характер. Для отримання необхідних прогнозних значень попиту використовуємо модель тригонометричного тренда якнайбільш адекватно описує реальний попит:
(1.6) де коефіцієнти На рис. 1 зображені графічно фактичні значення продажів вугілля за три роки з отриманим по формулою (6) прогнозом на планований період. Визначимо значення констант, використовуваних в моделі. Відомо, що обсяг майданчика в порту для зберігання вугілля W = 30000 т.; порт здатний щомісяця приймати до 15000 т., причому в період навігації пропускна спроможність порту зростає майже в 2 рази; ємність залізничного вагона V = 70 т. Фірма має 6 постачальників, n = 6, причому щомісяця кожен постачальник реально здатний поставити не більше 10000 т.; Експертним шляхом величини, що відповідають за надійність кожного постачальника, були вибрані наступним чином: р (1) = 0,9; р (2) = 0,9; р (3) = 0,8; р (4) = 0,8; р (5) = 0,7; р (6) = 0,7. Фірма повинна знайти стратегію поведінки, яка мінімізує функцію втрат (складається із затрат, пов'язаних з надходженням вугілля на склад b = 27; витрат зберігання h = 30; та штрафних втрат з = 100), а також підтримує бажаний рівень обслуговування ω = 0,82
Рис 1.1. Графік продажів з побудованим прогнозом.
Рис. 1.1. Фактичні та модельні рівні запасу вугілля. На рис. 1.2 представлені результати моделювання. На рис. 3 показаний запас (для різних значень початкового запасу), який матиме фірма в планованому періоді, якщо вона застосувати стратегію планування запасів, побудовану за моделлю. З графіка видно, що, яким би не був запас на початок періоду планування, з січня по травень рекомендується накопичувати вугілля. Це пов'язано з тим, що в травні починається період навігації, істотно зростає попит на вугілля, і для своєчасного його задоволення фірмі необхідно мати достатній запас. Потім запас плавно знижується, що пояснюється відповідним зниженням попиту.
Рис. 1.3. Рівень поточного запасу на 1999 р. (помісячно) при використанні стратегії, побудованої за пропонованої моделі для різних рівнів початкового запасу
У табл. 1 наведені значення відсотка дефіциту (відношення відкладеного попиту до пред'явленого) для різного запасу на початок року. Чітко простежується залежність між запасом на початок року і спостережуваним відсотком дефіциту: відсоток дефіциту збільшується (отже, зменшується рівень обслуговування споживачів) при зменшенні початкового запасу.
Отже, на основі наявних даних про постачання і відвантаження вугілля був проведений аналіз існуючої системи управління запасами на фірмі і,враховуючи виявлення характеристики даної системи, побудовано модель управління запасами вугілля. Щоб побудована модель управління запасами ефективно працювала, необхідно правильно оцінити величини всіх витрат, визначити надійність кожного постачальника і отримати якомога більш точний прогноз попиту, так як ці компоненти мають прямий вплив на вибір оптимальної стратегії. Ці завдання докладно не розглядаються, оскільки є лише необхідною ланкою на шляху до поставленої мети, кожна з них має самостійну теорію і вимагає глибокого детального аналізу. Аналіз структури попиту з даними про продажі вугілля за 1996-1998 рр.. показав, що попит має яскраво виражену сезонну складову, яка була представлена у вигляді тригонометричного тренда. Прогноз, отриманий по запропонованій нами моделі, був використаний при знаходженні оптимальної стратегії управління запасами. Результати моделювання показали, що система управління запасами, заснована на побудованій моделі управління запасами, підтримує бажаний рівень обслуговування споживачів протягом всього періоду планування при мінімальних очікуваних втратах, пов'язаних з надходженням вугілля в річковий порт, змертвінням капіталу в запасах і штрафом за несвоєчасно задоволений попит.
Заболотня К.О., Математичне моделювання управління запасами складських підприємств/ Заболотня К.О.// Вісник Бердянського університету менеджменту і бізнесу, “Економіка та управління підприємствами”. – Бердянск: БУМБ, – № 2 (18). – 2012. – С. 10-13.
У роботі було розглянуто економетричну модель, за допомогою якої можливо визначити розмір товарних запасів в залежності від витрат на рекламу, витрат на маркетингові дослідження, кількості укладених контрактів. При аналізі вихідних даних у пакеті прикладних програм STATISTICA 6.0 була виявлена наступна залежність між цими факторами:
Y1,2,3,4.5 = -137,12 +168,25 x +125,24 x + 21,52 x + 235,34 x. Основним показником точності рівняння регресії є стандартна помилка оцінки регресії (standart error of eslimate). Для нашого рівняння значення помилки досить мало й становить 0,013 за даними програми STATISTICA 6.0. Ще одним важливим фактором в оцінці регресійного рівняння є значимості коефіцієнтів. Якщо рівень значимості коефіцієнт перевищує фіксований рівень (для нашого рівняння фіксований рівень 0,05), то вплив даного фактору на обсяг реалізації незначимий. Програма вивела наступні коефіцієнти: для x1 – 0,002, для x2 – 0,01, для x3 – 0,008, для x4 – 0,006. Як видно із цього, всі обрані фактори значимі. Коефіцієнтом, що характеризує загальний вплив всіх обраних нами факторів на прибутком від реалізації товарів, є коефіцієнт множинної детермінації (у програмі R-squared). У даному випадку він дорівнює 0,99999. Це свідчить про правильний вибір факторів і про те, що прибуток від реалізації залежить від цих факторів на 99,9%. У результаті проведеного кореляційно-регресійного аналізу можна прийти до висновку, що між розміром товарних запасів й даними показниками спостерігається тісний зв'язок, а найвпливовішими показниками є витрати на рекламу й кількість укладених контрактів з іноземними партнерами. Отже, правильне управління товарними запасами суттєво впливає на фінансовий стан торговельного підприємства. Ефективний механізм управління товарними запасами торговельного підприємства дає змогу в повному обсязі реалізувати цілі та завдання, які стоять перед ним; сприяє результативному здійсненню всіх його функцій на підприємствах торгівлі. За допомогою математичних методів можна виробити правила управління запасами. Якщо для вирішення завдань управління запасами застосовуються математичні методи, то досліджувану систему необхідно описати за допомогою математичної моделі. Математичні моделі управління запасами дозволяють знайти оптимальний рівень запасів деякого товару, який допомагає мінімізувати сумарні витрати на покупку, оформлення й доставку замовлення, зберігання товару, а також збитки від його дефіциту.
Никитин А. В. Экономическое стимулирование управляющей системы оптово-торгового предприятия с целью снижения логистических издержек / А. В. Никитин // Информатика: проблемы, методология, технологии: материалы XI Международной научной конференции. — Воронеж: Изд-во ВГУ, 2011. — С. 56–62. Основними ознаками класифікації моделей управління запасами є: попит (витрата); параметри поповнення запасів; витрати, пов’язані з формуванням і підтриманням запасів; обмеження й стратегія управління. Відповідно до пропонованої класифікації розрізняють детерміновані та стохастичні (ймовірні) моделі управління запасами — в залежності від дії випадкових факторів на параметри системи управління. Якщо хоча б один параметр є випадковою величиною (процесом), модель буде стохастичною, в іншому випадку — детермінованою. Найбільш простим є випадок детермінованого статичного попиту. Проте такий вид споживання продукції зустрічається дуже рідко. Прикладом детермінованого статичного попиту може служити споживання сирої нафти на нафтопереробному заводі. Воно може змінюватися днями, але ці зміни будуть, як правило, настільки незначними, що припущення статичності попиту несуттєво спотворює дійсність. Найбільш складною з математичної точки зору є модель, у якій попит описується за допомогою імовірнісних нестаціонарних розподілів. Перевагою цієї моделі є найбільш точне відображення характеру попиту. Стохастична модель будується за тим же принципом, що й детерміновані моделі. Однак допускається незадоволений попит. Крім того, враховуються не тільки витрати на зберігання, а й транспортування товару. Так як реальні процеси дуже складні, то в зазначеній моделі прийняті три припущення: 1) незадоволений протягом строку виконання замовлення попит накопичується; 2) дозволяється не більше одного невиконаного замовлення; 3) розподіл попиту протягом строку виконання замовлення є стаціонарним (незмінним) у часі. Для визначення функції, що відображає сумарні витрати, віднесені до одиниці часу, введемо такі позначення: f (x) — щільність розподілу попиту х протягом строку виконання замовлення; D — очікуване значення попиту за одиницю часу; h — питомі витрати на зберігання (на одини- цю продукції за одиницю часу); p — питомі втрати від незадоволеного попиту (на одиницю продукції за одиницю часу); K — вартість розміщення замовлення; E (x) — функція зміни транспортних витрат залежно від обсягу попиту. Критерієм оптимальності також служить функція витрат за одиницю часу, яка складається з: 1. Вартості розміщення замовлень. Наближене число замовлень за одиницю часу дорівнює D / y, так що вартість розміщення замовлень за одиницю часу дорівнює KD / y. 2. Очікуваних витрат на зберігання.
Середній рівень запасу дорівнює:
Отже, очікувані витрати на зберігання за одиницю часу дорівнюють hl. Наведена формула отримана в результаті усереднення очікуваних запасів на початку і наприкінці тимчасового циклу, тобто величин y + M { R − x } і M { R − x } відповідно. При цьому ігнорується випадок, коли величина R − M { x } може бути від’ємною, що є одним із припущень цієї моделі, які її спрощують. 3. Вартість транспортних перевезень для задоволення попиту споживачів. Функція має ступінчастий вигляд, бо з ростом обсягу замовлення зростає вартість його перевезення:
4. Очікувані втрати, пов’язані з незадоволеним попитом. Дефіцит виникає при x > R. Отже, очікуваний дефіцит за одиницю часу дорівнює:
У моделі передбачається, що p очікувані втрати, які пропорційні обсягу дефіциту й пов’язані з незадоволеним попитом, за один цикл рівні pS. Оскільки одиниця часу містить D / y циклів, то очікувані втрати, обумовлені дефіцитом, складають pDs / y за одиницю часу. Результуюча функція загальних втрат за одиницю часу TCU має наступний вигляд:
Оптимальні значення y * та R * визначаються із наведених нижче рівнянь:
Наведена модель дає непогані результати і може застосовуватися для прогнозування на тому підприємстві, де відбувається безперервний контроль рівня запасів товару, оскільки попит на товар заданий своєю функцією щільності, тобто враховується його імовірнісний характер.
4.Ляшенко О. Використання моделей управління запасами, що підлягають природному убутку, як складових логістичних систем у діяльності підприємств / О. Ляшенко // Вісник Тернопільської академії народного господарства. Серія «Економіко-математичне моделювання». — Тернопіль: Економічна думка, 1999. — № 5. — С. 127–140.
Запаси підприємств визначають як резерв матеріальних цінностей. Вони є життєво важливою частиною будь-якої ділової активності. Як матеріальна форма оборотних активів, запаси є економічним ресурсом підприємства, який генерує дохід. Управління підприємством включає в себе дві основні функції, пов'язані з запасами. Перша – впровадити і підтримувати належну систему обліку та контролю за наявними запасами; друга – постійно прийм
|
||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.014 с.) |

 зує попит на вугілля на відрізку
зує попит на вугілля на відрізку  де
де 

 - прогнозні значення попиту на вугілля на відрізку t;
- прогнозні значення попиту на вугілля на відрізку t; - вектор замовлень, поданий в період t, де
- вектор замовлень, поданий в період t, де  (k) - замовлення k-му постачальнику в період t.
(k) - замовлення k-му постачальнику в період t.
 характеризує обсяг
характеризує обсяг .
.

 .
.  для
для 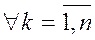 має наступний вигляд:
має наступний вигляд:


 незалежні
незалежні  , тоді спільний розподіл цих величин при векторі замовлень
, тоді спільний розподіл цих величин при векторі замовлень 
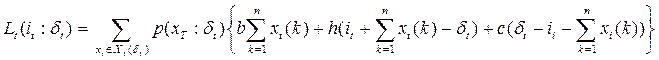 ,
, простір можливих реалізацій
простір можливих реалізацій Нехай
Нехай
 (1.1)
(1.1) де
де  (1.2)
(1.2) , Поданих у період t, і обсяг запасів it
, Поданих у період t, і обсяг запасів it де r(k) характеризує величину замовлення, яку реально здатний задовольнити k-ий постачальник за один період.
де r(k) характеризує величину замовлення, яку реально здатний задовольнити k-ий постачальник за один період.

 (1.3)
(1.3)
 q(k) цілі,
q(k) цілі,  ;
;
 то
то

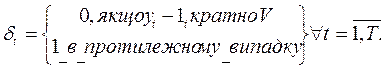 (1.4)
(1.4)

 ,
, (1.5)
(1.5)
 характеризує повні очікувані витрати за період, що залишився до кінця процесу планування замовлень, включаючи поточний період t, за умови, що залишилося T-t кроків, початковий рівень запасів в поточному періоді t дорівнює i, а при плануванні використовується оптимальна стратегія. На підставі принципу оптимума Беллмана, рекурентне співвідношення динамічних програмування для знаходження оптимальної стратегії, яка мінімізує побудовану цільову функцію, буде наступним:
характеризує повні очікувані витрати за період, що залишився до кінця процесу планування замовлень, включаючи поточний період t, за умови, що залишилося T-t кроків, початковий рівень запасів в поточному періоді t дорівнює i, а при плануванні використовується оптимальна стратегія. На підставі принципу оптимума Беллмана, рекурентне співвідношення динамічних програмування для знаходження оптимальної стратегії, яка мінімізує побудовану цільову функцію, буде наступним:


 має сенс ймовірності переходу зі стану, коли рівень запасів на початок відрізка t дорівнював i, у стані
має сенс ймовірності переходу зі стану, коли рівень запасів на початок відрізка t дорівнював i, у стані Рівень запасів на кінець відрізка t,
Рівень запасів на кінець відрізка t, - витрата, супутня цьому переходу
- витрата, супутня цьому переходу для кожного допустимого значення i. Тому будемо знаходити
для кожного допустимого значення i. Тому будемо знаходити  (з метою спрощення обчислень з кроком
(з метою спрощення обчислень з кроком  ), а в інших точках значення
), а в інших точках значення  визначаються інтерполяцією.
визначаються інтерполяцією.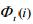 , при зростанні числа постачальників різко зростає тому, в цілях скорочення обчислень будемо знаходити
, при зростанні числа постачальників різко зростає тому, в цілях скорочення обчислень будемо знаходити 
 обчислюються методом найменших квадратів.
обчислюються методом найменших квадратів.