
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бункан дж. Ж. Научное управление запасами / дж. Ж. Бункан, Э. Ж. Кенигсберг – М. : наука, 1967. – с 38-43.Содержание книги
Поиск на нашем сайте
Моделі з фіксованим обсягом замовлення Принцип дії систем з фіксованим обсягом замовлення заснований на визначенні конкретний момент часу, коли потрібно розміщати замовлення, відповідають певному рівню запасу (крапці замовлення), — R, а також розміру цього замовлення Q. Крапка замовлення R — це завжди зовсім певна кількість матеріалу. Замовлення розміром Q розміщається в той момент, коли рівень запасу досягає крапки R. Рівень запасу визначається як залишок матеріалів перед минулою поставкою, плюс кількість отриманих матеріалів при минулій поставці, мінус витрачена кількість. Рішення, прийняте в моделях з фіксованим обсягом, можна сформулювати, наприклад, так: "коли рівень запасу знижується до 20, розмістити замовлення на 78 додаткових одиниць матеріалу". Дія моделі з фіксованим обсягом можна спрощено описати виходячи із припущення, що всі характеристики руху запасів відомі. Наприклад, якщо річна потреба в якихось виробів д3орівнює 100 штук, те це саме 100 штук, а не 100 ±10%. Те ж саме можна сказати про витрати на розміщення замовлення й витратах зберігання запасів. Незважаючи на те, що припущення про повну визначеність далеко не завжди реально, воно дає гарну основу для опису моделей руху запасів. Потреба в матеріалі постійна й рівномірно розподілена по всьому періоді. Час виконання замовлення (час із моменту видачі замовлення до одержання замовлених матеріалів) незмінний. Ціна одиниці матеріалів постійна. Витрати зберігання запасів розраховуються по середній величині запасу. Витрати на розміщення замовлення й пуско-наладочні витрати постійні. Для закупівлі будь-якої кількості матеріалу є необхідні ресурси й виключається можливість невиконання замовлення.
Малюнок 6.1 - Основна модель системи з фіксованим обсягом Уже втретє повторили!
Поточний запас матеріалу, як показано на малюнку 1.1 змінюється по "пилці" і, при його зниженні до рівня R (крапка замовлення), розмішається повторне замовлення. Замовлені вироби будуть отримані через інтервал часу L, що у даній моделі залишається незмінним. Спочатку для розробки моделі керування запасами необхідно встановити функціональний взаємозв'язок між цими змінними. У цьому випадку нас цікавлять загальні витрати на створення запасів, які можна виразити наступним рівнянням: Сумарні річні витрати = Річні витрати на закупівлі + Річні витрати на розміщення замовлень + Річні витрати на зберігання або
де ТС - сумарні річні витрати; D - річна потреба в матеріалі; С - ціна одиниці закуповуваного матеріалу; Q - кількість матеріалу, який необхідно замовити. Оптимальна кількість називається економічним розміром замовлення; S - витрати на розміщення одного замовлення; Н- річні витрати зберігання одиниці середнього запасу матеріалу. Найчастіше витрати на зберігання визначаються як відсоток від ціни матеріалу, тобто Н = ІЗ, де І - відсоток від ціни С. DC у правій частині рівняння являє собою Вартість закупівлі річної потреби матеріалу; (D/Q)S - річні витрати на розміщення замовлень (фактична кількість розміщених замовлень D/Q, помножена на витрати на розміщення одного замовлення S), а (Q/2)H - річні витрати зберігання (середній запас Q/2, помножений на річні витрати зберігання одного виробу Н). Залежності між цими величинами представлені в графічному виді на мал. 6.2. Потім для розробки моделі керування запасами необхідно визначити розмір замовлення Qopt при якій сумарні витрати мінімальні. Для знаходження крапки мінімальних витрат візьмемо похідну від сумарних річних витрат по Q і дорівняємо її до нуля.
Для розглянутого тут рівняння ці перетворення будуть мати такий вигляд:
R=dav L, де
dav — середня денна потреба в матеріалі (постійна величина); L — час виконання замовлення в днях (постійна величина). Модель з фіксованим обсягом у виробничому процесі Рівняння
(6.2)
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.223.239 (0.007 с.) |



 Малюнок 6.2 - Залежності різних складових витрат на створення запасу матеріалу від розміру замовлення.
Малюнок 6.2 - Залежності різних складових витрат на створення запасу матеріалу від розміру замовлення.
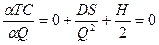
 (6.1)
(6.1)




