
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблеми управлыння запасами : матеріали симпозиума по управлінню запасами. – М. : цэми, 1972. –16-20 С.Содержание книги
Поиск на нашем сайте
Вплив знижок на розмір замовлення У багатьох компаніях і товариствах при замовленні збільшеного розміру поставок установлені знижки з оптової ціни. Замовляючи партії поставок більші від оптимального розміру, підприємство ризикує збільшенням вартості запасів. Проте воно може бути компенсоване зниженням закупівельної ціни. Загальна вартість закупки та запасів (М) з урахуванням знижок визначається так:
де Сh - змінна вартість зберігання одиниці продукції в запасі за рік; Со - змінна вартість подачі одного замовлення; Якщо закупівельна ціна постійна і не залежить від розміру замовлення, включення вартості закупленої продукції (СD) у рівняння загальної вартості приводить до переміщення цього рівняння паралельно осі без зміни її форми. При цьому критична точка оптимального замовлення (ЕОQ) не переміщується. Якщо товар реалізується за ціною С за одиницю, але для замовлень, розмір яких перевищує певну величину q І, надається знижка, відповідно до якої ціна за одиницю продукції знижується до величини СІ,. змінюється крива загальної вартості. При цьому розмір замовлення qІ може перевищувати оптимальний q0. Але для прийняття рішення про розмір замовлення треба провести відповідні розрахунки, Знижка може бути прогресивною, тобто збільшуватися при подальшому зростанні розміру разового замовлення. Тому треба провести розрахунки загальної вартості по кожному варіанту ціни. Для ілюстрації розрахунків використаємо попередній приклад. Підприємство одержує в рік D = 4000 одиниць продукції за ціною С = 500 гривень. Вартість зберігання одиниці запасів Сh = 600 грн., а вартість подачі одного замовлення Со = 1200 грн. Оптимальний розмір замовлення в цих умовах складає ЕОQ = 126,5 одиниць при сукупних витратах на зберігання ТС = 75894,66грн. За умовами поставки надається знижка 4%, якщо рівень замовлення знаходиться в межах 200 - 499 одиниць і в розмірі 6%, якщо рівень замовлення становить 500 і більше одиниць (табл.11.1). Виходячи з цих умов, слід перевірити доцільність використання знижок. При цьому враховується, що зі збільшенням розміру замовлення вартість продукції на одиницю зменшиться, знизиться також вартість замовлення, але зростуть витрати на зберігання. У початковому варіанті загальна вартість закупки та запасів (М) складає:
Таблиця 11.1 - Знижки з ціни за одиницю продукції залежно від розміру замовлення
Розрахуємо загальну вартість другого варіанта, при якому розмір замовлення має бути не менше 200 одиниць. Тоді загальна вартість закупки та запасів буде:
За третім варіантом загальна вартість досягає величини:
Таблиця 11.2 - Порівняння мінімальних значень загальної вартості
На практиці більшість систем управління запасами має певний елемент невизначеності як по відношенню до часу поставки, так і відносно попиту. Для вирішення цих проблем неможливо використовувати математичні моделі, які допомагали б у вирішенні більш простих задач. Такі складні задачі можуть вирішуватися методами імітаційного моделювання. Але при певних обмеженнях нарощування складності моделі, викликаної невизначеністю значень часу поставки замовлень або попиту, можна побудувати математичну модель, яка достатньо правильно відображає існуючу ситуацію.
12.Хачатрян В. И. Математические методы управления запасами: [Текст лекций] / В. И. Хачатрян – М.: МЭСИ, 2000. С. 25-29 Приклад 12.1 Серед інших товарів особистої гігієни фірма "Юсі" реалізує зубну пасту "Колгейт". Обсяг реалізації - 273 000 тюбиків у рік. Величина попиту рівномірно розподіляється протягом року. Закупівельна ціна однієї упаковки - 6,52 грн. Оформлення одного замовлення обходиться фірмі в 2150 грн. Термін доставки замовлення від постачальника становить 5 робочих днів (при п'ятиденному робочому тижні). Згідно з даними управлінського обліку витрати на зберігання становлять 20 % закупівельної ціни товарів. Кількість робочих днів у році - 260. Дати рекомендації керівництву підприємства з управління запасами.
Розв'язання Визначимо оптимальний розмір закупівель, що мінімізує вартість запасів, і часовий інтервал між ними. Для розрахунку розміру запасу скористаємося формулою (12.1):
Мінімальне річне значення додаткових витрат, пов'язаних із замовленням партії товарів та їх зберіганням, визначиться за формулою (12.2):
Загальна вартість закуплених 273 000 упаковок зубної пасти "Колгейт" (ЗВЗ) у рік становитиме:
Отже, вартість завозу та зберігання зубної пасти становитиме лише 2,1 % (38 850: 1 818 810 Якби менеджер з закупок подавав замовлення на партію в 28 000 тюбиків, то зберігання запасів обійшлося б фірмі в 39 218 грн:
Таким чином, як показують розрахунки, розмір партії для мінімізації витрат на зберігання має бути оптимальним. Оформлення нового замовлення керівник відділу закупівель повинен здійснювати кожного разу після закінчення періоду, який дорівнює:
Оскільки в році 260 робочих днів, часовий інтервал між замовленнями становитиме:
Обсяг продажу зубної пасти за 5 днів, протягом яких здійснюється поставка замовлення розраховується за формулою (12.3) і визначиться так:
Отже, замовлення на поставку чергової партії зубної пасти слід проводити в той момент, коли рівень її запасів на складі знизиться до 5250 тюбиків. Другий метод обчислення оптимального розміру замовлення ґрунтується на складанні таблиці розрахунку очікуваної вартості партії при її альтернативних розмірах. Для її складання використаємо подану раніше інформацію: o ціна 1 тюбика пасти - 6,52 грн; o вартість зберігання 1 тюбика пасти - 20 % від 6,52 грн, тобто 1,3 грн; o витрати на оформлення одного замовлення - 2160 грн. Таблиця сукупної вартості замовлень різної величини матиме такий вигляд (табл. 12.1).
Таблиця 12.1 Розрахунок очікуваної вартості партії при її альтернативних розмірах
Зроблені розрахунки свідчать про те, що оптимальним є замовлення розміром в 30 000 тюбиків пасти (той же результат був отриманий при розрахунках, виконаних першим методом). У цьому випадку спостерігається рівність витрат на зберігання і витрат, пов'язаних з оформленням замовлень. Наявність у таблиці невеликої розбіжності даних (19 500 і 19 350 грн відповідно) пояснюється допущеними при рішенні задачі округленнями отриманих результатів. Порівняно з іншими альтернативами оформлення замовлення в обсягу 30 000 тюбиків і його подальше зберігання зажадають від торгової організації мінімальних витрат у розмірі 38 850 грн. Третій, графічний метод оптимізації розміру замовлення полягає в тому, що по осі абсцис відкладаємо альтернативні варіанти обсягу замовлення, по осі ординат - відповідні їм витрати у гривні (рис. 12.1). Користуючись даними табл. 12.1, будуємо графік поведінки витрат, пов'язаних зі зберіганням запасу товарів. Дані були взяті з рядка 3 табл. 12.1. Будучи пропорційними, ці витрати зростуть лінійно при збільшенні обсягу закупівель (пряма у^. Графік у2 ілюструє поведінку витрат, пов'язаних з оформленням замовлень. Дані для його побудови були взяті з рядка 4 табл. 12.1. Зі зростанням обсягу замовлень річні витрати на їх оформлення знижуються. Видно, що перетинаються у1 і у2 у разі оформлення замовлення розміром в 30 000 тюбиків пасти. Нарешті, третій графік (у3) ілюструє поведінку сукупних витрат фірми з оформлення замовлень і подальшого зберігання сформованих запасів товару. В діапазоні обсягу закупівель від 20 000 до 30 000 тюбиків ця крива має тенденцію до зниження. Закупівля в 30 000 шт. є "критичною". Пройшовши цю точку, сукупні витрати починають зростати.
Рис.12.2 .Графічний метод оптимізації розміру замовлення Таким чином, розрахунки, здійснені трьома методами, дають змогу зробити такі висновки: оптимальними для фірми є закупівля товару обсягом в 30 000 тюбиків зубної пасти, оскільки в цьому випадку витрати з оформлення замовлень партії товару та їх подальшого зберігання будуть мінімальними. Оформлення замовлення при наданні знижок. При оформленні замовлення на поставку товару контрактна ціна може залежати від обсягу закупівлі: на замовлення великого обсягу, як правило, надаються знижки. Замовлення більших партій товарів ведуть до збільшення вартості запасів, проте це збільшення деякою мірою може бути компенсоване зниженням закупівельної ціни. З'ясуємо, як вплине надання знижки на загальну вартість запасів. Приклад 12.2 (на основі даних прикладу 12.1) Закупівля зубної пасти "Колгейт" має проводитися партіями в 30 000 тюбиків за ціною 6,52 грн. за одиницю (див. приклад 22.1). Припустимо, що постачальником пропонується така система знижок (табл. 12.2). Чи слід фірмі скористатися однією зі знижок? Чи буде компенсовано збільшення витрат на зберігання запасів зниженням закупівельних цін? Таблиця 12.2. Система знижок, пропонована постачальником
Розглянемо два варіанти закупівлі. У першому випадку партія товару (д), що замовляється, становитиме 50 000 шт., що припускає закупівельну ціну в 6,39 грн за тюбик. У другому випадку розмір партії становитиме 80 000 шт., отже, закупівельна ціна буде знижена до 6,26 грн за тюбик. Розв'язання При q = 50 000 шт. і Ц - 6,39:
Вартість закупівлі, зберігання і придбання товару становитиме:
При q = 80 ООО шт. і Ц - 6,26 отримаємо:
Порівняємо альтернативні варіанти управлінських рішень па основі даних, наведених у табл. 12.3. Таблиця 12.3. Порівняння альтернативних варіантів управлінських рішень щодо закупівель
Проведені розрахунки свідчать про те, що фірмі найбільше вигідна третя альтернатива, що припускає замовлення у розмірі 80 000 тюбиків. Порівняно з першим варіантом (замовлення 30 000 тюбиків) істотно зростуть витрати на зберігання запасів (52 000 грн проти 19 500 грн). Проте це зростання компенсується економією на закупівельних цінах. Якщо в першому випадку постачальнику буде перераховано 1 779 960 грн, то за третьою альтернативою кредиторська заборгованість фірми становитиме 1 708 980 грн. Більш ніж у два рази знизяться і витрати на оформлення замовлень. Якщо в першому випадку ця сума за рік становитиме 19 350 грн, то при закупівлі партії у 80 000 упаковок оформлення замовлень обійдеться фірмі в 7337 грн. Таким чином, порівняно з першим, базовим, варіантом третя альтернатива надасть можливість фірмі знизити загальну вартість запасу товару на 50 493 грн у рік (1 818 810 грн - 1 768 317 грн). Проте подібне управлінське рішення може бути ухвалене лише за наявності в організації відповідних фінансових можливостей і складських приміщень.
Необхідно зазначити, що наведені вище розрахунки можуть бути застосовані й до підприємств, що займаються виробництвом продукції. В такому випадку формула (12.5) набуває вигляду:
Якщо у формулі (12.6) вартість подачі одного замовлення (£0) замінити на вартість організації виробничого циклу (5Я), то формула матиме вигляд:
де о - розмір партії продукції. Очевидно, що за аналогією з попередньою моделлю ДВ набуває свого мінімального значення, якщо:
Отриману оптимальну кількість продукції в партії називають економічним розміром партії.
13. Хенссменн Ф. Применение математических методов в управлении производством и запасами / Ф. Хенссменн: [Перев. с англ. Д. Б. Юдина]. – М.: Прогресс, 1966. – 208-215с.
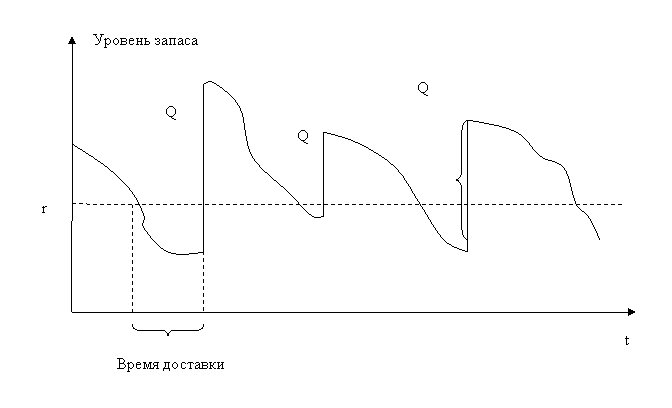
Разработка стохастической модели упраления запасами с непрерывным контролем уровня запаса в условиях случайного спороса Выделяют две основные системы управления запасами: систему с постоянным контролем и систему с периодическими проверками. В системе с периодическими проверками подсчет запаса производится периодически (раз в день, неделю, месяц), и в зависимости от уровня наличного запаса производится заказ определенной партии продукции. При наличии автоматизированной системы учета, система управления запасами может основываться на модели управления запасами с постоянным контролем уровня запаса, т.е. система, в которой каждый раз, когда уровень запаса опускается до r, подается заявка на заказ размером Q. При детерминированном и случайном спросе динамика запаса описывается рисунками 13.1 и 13.2 соответственно.
Рисунок 13.1 – Динамика уровня запасов при детерминированном спросе
Рисунок 13.2 – Динамика уровня запасов при случайном спросе Для разработки автоматизированной системы управления запасами была выбрана модель с непрерывным контролем, предложенная Хедли и Уайтином, скорректированная на неудовлетворенный спрос. Кроме того, модифицируем данную модель на величину транспортных расходов и дифференциальные скидки в зависимости от объема заказа. Последнее условие является крайне важным для любого предприятия, так как возможность покупки большего объема товаров по меньшей цене помогает снизить затраты. В некоторых случаях снижение оказывается существенным.
Так как реальные процессы слишком сложные, то в рассматриваемой модели приняты три допущения.
Для определения функции, отражающей суммарные затраты, отнесенные к единице времени, введем следующие обозначения.
Критерием оптимальности также служит функция затрат в единицу времени, которая складывается из:
Приведенная формула получена в результате усреднения ожидаемых запасов в начале и конце временного цикла, то есть величин у + M{R-х} и M{R-х} соответственно. При этом игнорируется случай, когда величина R - М{х} может быть отрицательной, что является одним из упрощающих допущений рассматриваемой модели.
(13.3)
Результирующая функция общих потерь за единицу времени TCU имеет следующий вид.
Оптимальные значения у* и R* определяются из представленных ниже уравнений.
Для нахождения y* и R, используем численный алгоритм, предложенный Хедли и Уайтином, слегка модифицировав его. Шаг 0. Находим y(j) как Шаг i. Для каждого y(j), находим R(j) на i-м шаге. Критерий выхода: Следует также учесть особенности предприятий, для которых разрабатывается система. Так как пиво является сезонным товаром, то это должно быть каким-то образом учтено. В магистерской работе был разработан следующий подход. На основе статистических данных выделяются так называемые "пики" спроса, т.е. интервалы с минимальным и максимальным значениями. После чего весь данные за год разбиваются на четыре участка относительно минимума и максимума. По полученным выборкам на основе интерполяцонной формулы Лагранжа строятся четыре функции плотности, соответствующие имеющимся сезонам. И потом в зависимости от того, на какую часть года приходится день, для которого требуется найти объем заказа, используется та или иная функция. На рис.3.3 демонстрируется схема построения функций плотности спроса по сезонам. В качестве примера был выбран максимальный пик, который приходится на теплые месяцы (а если конретнее, то на период апрель-сентябрь).
Р исунок 13.3 - Схема построения функции плотности спроса по сезонам. Анимированное изображение (13 кадров, 12 циклов повторений). Алгоритм работы автоматизированной системы управления запасами выглядит следующим образом:
Рисунок 13.4 -Алгоритм функционирования системы управления запасами Данная система еще не может быть использована на практике, так как в ней рассматривается только один продукт. Реальные системы управления запасами должны быть многономенклатурными. Поэтому в рамках выпускной работы магистра планируется добавить в систему механизмы решения следующих задач:
14. [14, с.14-15]
В моделі управління запасами з імовірнісним попитом за відсутності витрат на оформлення замовлення очікувані витрати
Доведено, що
Тобто
В моделі управління запасами з імовірнісним попитом за наявності витрат на розміщення замовлення, використовуючи позначення, введені вище, отримуємо вираз для сумарної очікуваної вартості:
У свою чергу,
15. [14, с.15-17]
Розглянемо багатоетапну модель, яка не враховує вартість розміщення замовлення, та передбачає можливість заборгованості і миттєву поставку. Передбачається також, що попит Припустимо, що горизонт планування охоплює
Тоді:
де Принагідно відмітимо, що величина Якщо кількість етапів є нескінченною (нескінченний горизонт планування), рівняння (1.2) набуває вигляду:
де
Виходячи з (1.3), а також враховуючи, що
16. [14, с. 21-23]
Модель конкурсного механізму розподілу ресурсу характеризується участю агентів у змаганні щодо отримання ресурсу на пільгових умовах. Як приклад такого механізму розподілу, можна назвати, наприклад, тендерний розподіл наявних ресурсів. У моделі конкурсного механізму розподілу ресурс одержують тільки переможці конкурсу, тому що на всіх агентів наявних ресурсів може не вистачити. Агенти повідомляють центру дві величини: обсяг необхідного ресурсу Впорядкувавши агентів у порядку зменшення ефективності Для цього вводиться система штрафів:
де коефіцієнт Коефіцієнт
де
Якщо реальна ефективність виявилась вище очікуваної, то штрафи дорівнюють нулю, або додатково можуть прийматись рішення щодо преміювання агента. Ресурс Відзначимо, що в разі використання такої процедури перемога в конкурсі залежить тільки від величини ефективності При наявності функції штрафів конкурсні механізми забезпечують оптимальний розподіл ресурсів, але для центру такий механізм розподілу не завжди прийнятний, тому що не всі агенти отримують свої заявки, а за наявності розгалужених торгових мереж центру доводиться фінансувати і агентів, які не отримали своїх заявок для збереження існуючої мережі. Особливо таке уточнення важливе для систем з коаліційною участю агентів. 17. [14, с. 23-24]
Модель пріоритетного механізму розподілу. У цій моделі розподілу ресурсу, як випливає з її назви, при формуванні планів (рішенні про те, скільки ресурсів (запасів) виділити тому або іншому агенту) істотно використовуються показники пріоритету агентів. Пріоритетні механізми в загальному вигляді описуються такою процедурою:
де
тобто, вибирається таким чином, щоб при даних заявках і функціях пріоритету в умовах дефіциту розподілявся повністю весь запас Ми вважаємо доцільним серед пріоритетних механізмів, залежно від виду функції пріоритету, виділити такі механізми: · прямих пріоритетів, де · абсолютних пріоритетів, у яких пріоритети агентів фіксовані і не залежать від заявок; · зворотних пріоритетів, де 18. [15, с.10-17]
“Оптимізація управління запасами торгових підприємств” здійснено економіко-математичну постановку та реалізацію задач оптимізації управління запасами складських і гуртових підприємств, проведено аналіз результатів модельних експериментів. У роботі здійснено побудову економіко-математичної моделі управління запасами на основі теорії оптимального управління. Розв’язок поставленої задачі дає змогу визначити оптимальну траєкторію системи запасів при заданій стратегії управління. Така задача особливо актуальна для дослідження запасів торгових підприємств у динаміці. Задача оптимального управління запасами полягає у визначенні оптимального процесу або послідовності станів системи
де M – множина допустимих процесів управління запасами; Т – тривалість періоду дослідження системи запасів; z(t)=(z1(t), z2(t), …, zn(t)) – вектор запасів продукції на складі; q(t)=(q1(t), q2(t), …, qn(t)) – вектор обсягів замовлень продукції, яка повинна бути доставлена постачальниками на склад; d(t)=(d1(t), d2(t), …, dn(t)) – вектор обсягів попиту на продукцію кожного виду; c(t) – вектор витрат на зберігання одиниці продукції кожного виду протягом часового періоду (ti, ti+1); p(t) – вектор витрат на замовлення одиниці продукції кожного виду; α і β – вагові коефіцієнти, які вказують на пріоритет кожного з доданків функціоналу оцінювання. Допустимий процес управління системою запасів v(t) задовольняє обмеження, які мають такий загальний вигляд:
(z(t), q(t), d(t))
де Vt – деяка підмножина 3n -вимірного евклідового простору R3n. Обмеження на процес управління системою запасів мають вигляд: 1) розмір запасу z(ti+1), який перебуває на складі в момент часу ti+1, залежатиме від величини запасів у попередній момент часу z(ti), кількості продукції, яку поставили на склад (величини замовлення) q(ti) та величини попиту на цю продукцію d(ti), тобто: z(ti+1)=z(ti)+q(ti)-d(ti); (18.3) 2) величина замовлення q(ti+1) залежить від величини запасу z(ti) та величини попиту d(ti): q(ti+1)=f(z(ti), d(ti)). (18.4)
Для визначення виду функціональної залежності у рівнянні (4) пропонуємо використати формулу Уілсона:
де γ(t) – вектор коефіцієнтів врахування величини запасів у попередній момент часу; 3) задані початкові умови
4) задані кінцеві умови
Для визначення траєкторії системи запасів при заданих кусково-лінійних функціях управління використовують наближені методи розв’язування задачі Коші, зокрема, метод Ейлера, методи Рунге-Кутта. Розв’язок задачі оптимального управління запасами можна знайти за допомогою відомих методів знаходження розв’язку загальної задачі оптимального управління, зокрема, за методом Лагранжа-Понтрягіна, за допомогою достатніх умов оптимальності. У випадку, коли неможливо знайти оптимальний процес управління запасами, необхідно визначити мінімізуючу послідовність при умові, що функціонал оцінювання обмежений знизу на множині М. Також у дисертаційній роботі запропоновано застосовувати економетричний підхід до управління запасами гуртових та складських підприємств, а саме структурне моделювання з використанням симультативних моделей. Структурне моделювання дозволяє врахувати двосторонній зв’язок між економічними змінними, провести аналіз структурних параметрів, що показують величину приросту результуючої ознаки, пов'язану з приростом факторної ознаки, оцінити прямий та непрямий вплив факторних змінних на результуючі, провести оцінку тісноти зв’язку між змінними, побудувати прогноз на майбутній період. Одними з найважливіших показників, які характеризують роботу торгового підприємства в короткостроковому періоді, виступають обсяги замовлення та розміри запасів товарів на складі. Між цими економічними змінними існує двосторонній зв’язок, оскільки розміри запасів товару на складі впливають на обсяги замовлень на товар у постачальників, і, навпаки, обсяги замовлень на товар зумовлюють розміри запасів. Дослідження системи запасів проводимо в короткостроковому періоді та вважаємо, що ціна товару практично не змінюється, і тому не беремо її до розг
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.21.161 (0.013 с.) |

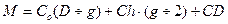 ,
, грн
грн
 грн.
грн. грн..
грн..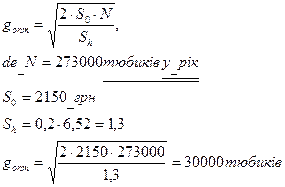


 100) загальної річної вартості її запасу.
100) загальної річної вартості її запасу.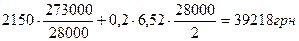 .
.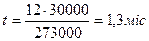
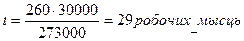




 .
.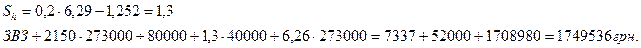





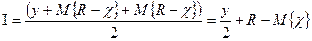





 , R0=0. Переходим к i-шагу.
, R0=0. Переходим к i-шагу. , i=i+1.
, i=i+1.


 розраховуються за формулою:
розраховуються за формулою: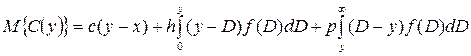 .
. є функцією випуклою по
є функцією випуклою по  , а тому має єдиний екстремум в точці
, а тому має єдиний екстремум в точці  .Дослідивши функцію на екстремум отримуємо:
.Дослідивши функцію на екстремум отримуємо: ,
, .
. визначається з рівняння:
визначається з рівняння: (14.1)
(14.1)
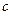 - вартість закупівлі (або виробництва) одиниці продукції,
- вартість закупівлі (або виробництва) одиниці продукції, - вартість розміщення замовлення,
- вартість розміщення замовлення, - питомі витрати на зберігання одиниці продукції протягом даного періоду,
- питомі витрати на зберігання одиниці продукції протягом даного періоду, - питомі втрати від незадоволеного попиту (на одиницю продукції за даний період),
- питомі втрати від незадоволеного попиту (на одиницю продукції за даний період), - величина випадкового попиту за даний період,
- величина випадкового попиту за даний період, — щільність ймовірності попиту за даний період,
— щільність ймовірності попиту за даний період, - обсяг замовлення,
- обсяг замовлення, - наявний запас продукту перед розміщенням замовлення.
- наявний запас продукту перед розміщенням замовлення. .
. етапів і незадоволений попит може залишатися таким лише впродовж одного етапу. Нехай:
етапів і незадоволений попит може залишатися таким лише впродовж одного етапу. Нехай: - максимальний сумарний очікуваний прибуток для етапів від
- максимальний сумарний очікуваний прибуток для етапів від  до
до  , визначений за умови;
, визначений за умови;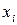 — рівень наявного запасу перед розміщенням замовлення на і-му етапі;
— рівень наявного запасу перед розміщенням замовлення на і-му етапі; ‑ питомий дохід від реалізації одиниці продукції, модель вигляду задачі динамічного програмування.
‑ питомий дохід від реалізації одиниці продукції, модель вигляду задачі динамічного програмування. (15.1)
(15.1) ,
, 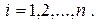
 незадоволений попит на і-му етапі, який повинен бути задоволений на (і+1)-му етапі. Задачу можна розв’язати відомими методами динамічного програмування.
незадоволений попит на і-му етапі, який повинен бути задоволений на (і+1)-му етапі. Задачу можна розв’язати відомими методами динамічного програмування.
 буде опуклою):
буде опуклою):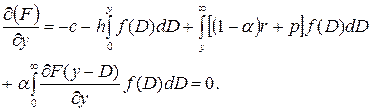 (15.2)
(15.2)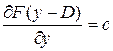 , співвідношення для визначення оптимального рівня замовлення
, співвідношення для визначення оптимального рівня замовлення  .
. і оцінку
і оцінку  очікуваної ефективності його використання. Очікуваний ефект для системи в цілому від діяльності і-го агента в цьому випадку дорівнює
очікуваної ефективності його використання. Очікуваний ефект для системи в цілому від діяльності і-го агента в цьому випадку дорівнює  . У ролі
. У ролі  виступає, як правило, ціна товару. Тобто торгові точки, розміщені у великих містах або індустріальних зонах, мають деяку перевагу, виходячи з більш високих доходів населення.
виступає, як правило, ціна товару. Тобто торгові точки, розміщені у великих містах або індустріальних зонах, мають деяку перевагу, виходячи з більш високих доходів населення. і розуміючи, що агенти можуть зробити неадекватні заявки, необхідно організувати жорстку систему контролю за виконанням взятих зобов'язань.
і розуміючи, що агенти можуть зробити неадекватні заявки, необхідно організувати жорстку систему контролю за виконанням взятих зобов'язань. ,
, ідентифікується як «жорсткість» штрафу.
ідентифікується як «жорсткість» штрафу. від її реального значення –
від її реального значення – 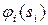 . Величина
. Величина  , власне, визначає величину обману, на який свідомо йде агент заради перемоги в конкурсі. Цільова функція агента в такому випадку набуває вигляду:
, власне, визначає величину обману, на який свідомо йде агент заради перемоги в конкурсі. Цільова функція агента в такому випадку набуває вигляду: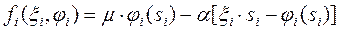 ,
,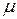 – коефіцієнт ефективності використання ресурсу агентом;
– коефіцієнт ефективності використання ресурсу агентом; – його прибуток.
– його прибуток. , що є у розпорядженні центру, розподіляється між n агентами таким чином: перший агент
, що є у розпорядженні центру, розподіляється між n агентами таким чином: перший агент 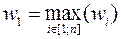 одержує ресурс у повному обсязі згідно з відповідною заявкою
одержує ресурс у повному обсязі згідно з відповідною заявкою  . Потім одержує ресурс в обсязі
. Потім одержує ресурс в обсязі  агент з меншою ефективністю і так далі, поки не закінчиться весь ресурс
агент з меншою ефективністю і так далі, поки не закінчиться весь ресурс 
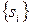 - вектор їх заявок,
- вектор їх заявок, - вектор обсягів запасів, які виділяються агентам,
- вектор обсягів запасів, які виділяються агентам,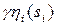 - функція пріоритету агентів,
- функція пріоритету агентів,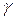 - нормуючий параметр, який вибирається з умови бюджетних обмежень
- нормуючий параметр, який вибирається з умови бюджетних обмежень ,
, .
. – зростаюча функція заявки
– зростаюча функція заявки  ;
;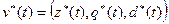 , що надає мінімум функціоналу
, що надає мінімум функціоналу
 , (18.1)
, (18.1) Vt для t = 0, t1, t2, …, T, (18.2)
Vt для t = 0, t1, t2, …, T, (18.2) , (18.5)
, (18.5) ,
, ; (18.6)
; (18.6) ,
, . (18.7)
. (18.7)


