
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кудрявцев Б. М. Модели управления запасами / Б. М. Кудрявцев, Ю. А. Беляев, Н. Н. Голдобина – М. : ин-т управления им. С. Орджоникидзе, 1987. – С. 32-38.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Классическая модель экономического заказа. Классическая модель наиболее экономичного размера партии представляет собой простейшую модель определения оптимального размера заказа. Основные предположения:
Исходя из этих предположений, размер заказа всегда будет одинаков, а уровень наличного запаса в момент поступления пополнения всегда один и тот же. Поскольку спрос неслучаен, а время поставки постоянно, в системе при поступлении требований отсутствует дефицит. Средние годовые издержки (TCU), зависящие от стратегии функционирования, включают фиксированные издержки, связанные с подачей заказа (K) и издержки содержания запаса (h), кроме того, учитывается закупочная стоимость товара (C). Издержки содержания запаса за цикл длинной T определяются по формуле (2.1):
где s – наличный запас в системе в момент поставки;
Средние годовые издержки определяются по формуле (9.3):
Найдем минимум функции TCU(Q):
откуда
где Q* – оптимальный размер заказа. Формула (18.5) дает ответ на вопрос, сколько заказывать, ответ на вопрос, когда необходимо делать заказ дает точка заказа (т.е. уровень запаса в момент подачи заявки), определяемая формулой (18.6):
где m – наибольшее целое число, меньшее или равное τ/T. Каждый раз, когда наличный запас достигает уровня r подается заказ на Q единиц, как показано на рисунке 9.1.
Pисунок 9.1 – Динамика уровня запаса В рассмотренной системе пополнение запаса происходило мгновенно [7], в виде поступления партии размером Q. Но поступление может происходить не мгновенно, а с определенной интенсивностью μ. При этом интенсивность поступления продукции составляет μ единиц в год, а интенсивность спроса на эту продукцию – λ единиц в год. Тогда, с учетом данных обозначений, формулу (9.3) можно переписать следующим образом:
Оптимальный размер заказа и точка заказа определяются по формулам (9.8) и (9.9).
Дискретный спрос. В большинстве случаев на практике значение Q* достаточно велико, и потому можно считать объем спроса непрерывной величиной и округлять Q* до ближайшего целого. Но в случае медленно оборачивающихся запасов это предположение перестает действовать. В этом случае считается, что требования дискретны, а Q* – целое число. Тогда оптимальный объем заказа определяется исходя из условия (9.10):
Оптимальным значением Q* является Q=1 или, для Q>1, наибольшее Q для которого выполняется условие (9.11):
Отсюда, Q* является наибольшим положительным целым значением Q, для которого выполняется соотношение (9.12):
Пусть ts – время между подачей требований, а
Тогда точка заказа r определяется как наибольшее целое число, меньшее или равное Детерминированный нестационарный спрос Данная модель строится на тех же предположениях, что и классическая модель управления запасами. Однако, предполагается, что с предыдущих периодов может оставаться неизрасходованный запас. Поэтому задача из однофакторной становится двухфакторной: требуется найти такой уровень заказа и остатка с предыдущего периода, при которых общая функция средних издержек была бы минимальна:
Оптимальный уровень запаса определяется в модели при помощи методов динамического программирования. Причем, алгоритм является достаточно трудоемким. Модель со случайным спросом. Все модели, которые были рассмотрены до этого являются системами с постоянным уровнем спроса, что на практике встречается редко. Поэтому стали разрабатываться модели управления запасами на основе случайного спроса. Рассмотрим детерминированную модель экономичного размера заказа для случайного спроса. При этом используется приближенный метод, который предполагает существование постоянного буферного запаса на протяжении всего планового периода. Размер резерва устанавливается так, чтобы вероятность истощения запаса в течение периода выполнения заказа (интервала между моментом размещения заказа и его поставкой) не превышала наперед заданной величины. Введем следующие обозначения.
Основным предположением при построении модели является то, что величина спроса Х1 на протяжении срока выполнения заказа L является нормально распределенной случайной величиной со средним μ1 и стандартным отклонением σ1, т.е. имеет распределение N(μ1, σ1) На рисунке 9.2 показана зависимость между размером резервного запаса В и параметрами детерминированной модели экономичного размера заказа, которая включает срок выполнения заказа L, среднюю величину спроса μ1 а протяжении срока выполнения заказа и экономичный размер заказа у*. Заметим, что L должно быть равно эффективному времени выполнения заказа.
Вероятностное условие, которое определяет размер резервного запаса В, имеет вид:
По определению случайная величина
является нормированной нормально распределенной случайной величиной, т.е. имеет распределение N(0, 1). Следовательно,
На данном этапе авторами была введена случайная величина Кαа, которая определяется из таблицы стандартного нормального распределения, таким образом что:
Следовательно, размер резервного запаса должен удовлетворять неравенству
Величина спроса на протяжении срока выполнения заказа L обычно описывается плотностью распределения вероятностей, отнесенной к единице времени (например, к дню или неделе), из которой можно определить распределение спроса на протяжении периода L. В частности, если спрос за единицу времени является нормально распределенной случайной величиной со средним D и стандартным отклонением σ, то общий спрос на протяжении срока выполнения заказа L будет иметь распределение N(μL, σL), где μL=DL и Формула для σL получена на основании того, что значение L является целым числом (или же округлено до целого числа).
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.46.90 (0.007 с.) |

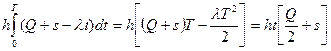
 (9.1)
(9.1)
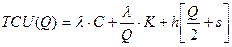
 (9.4)
(9.4) (9.5)
(9.5) (9.6)
(9.6)
 (9.7)
(9.7) (9.8)
(9.8) (9.9)
(9.9) (9.10)
(9.10)
 (9.12)
(9.12) – время от момента подачи заказа до момента поставки очередного заказа, определяемое по формуле (9.13):
– время от момента подачи заказа до момента поставки очередного заказа, определяемое по формуле (9.13): (9.13)
(9.13) (9.14).
(9.14).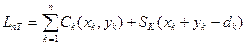 (9.15)
(9.15) (9.16)
(9.16)
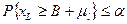 (9.17)
(9.17) (9.18)
(9.18) (9.19)
(9.19) (9.20)
(9.20) (9.21)
(9.21)



