
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютные величины, их виды, способы получения и измерения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Характеристика изучаемых экономических и социальных явлений проводится с помощью статистических показателей. Статистические показатели – это величины, адекватно (соответственно) характеризующие отображаемое явление в условиях качественной определенности. Качественная определенность показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью.
Рассмотрение изучаемого объекта во всех его связях и отношениях приводит к тому, что для получения целостной статистической характеристики изучаемого явления применяется система статистических показателей. Важнейшая особенность системы статистических показателей – содержательное единство показателей, обусловленное изучением единого объекта. Система экономико-статистических показателей в управлении предприятием призвана выполнять четыре основные функции: директивную, учётную, стимулирующую и информационную. Изучая отчётные данные по действующей системе показателей, руководители разного уровня управления должны получать объективную информацию о реальном состоянии и тенденциях развития организаций, отраслей и экономики в целом. Плановые показатели, осуществляя директивную и стимулирующую функции, призваны ориентировать руководителей и работников предприятий на выполнение поставленных задач. Значительное различие на практике величин плановых и учётных показателей требует проведения комплексного и всестороннего анализа деятельности предприятий. С помощью анализа выявляются неиспользованные резервы, определяются пути устранения выявленных недостатков в работе и т.д. В процессе статистического наблюдения получают данные о значениях различных признаков, характеризующих каждую единицу совокупности. Для характеристики совокупности в целом или отдельных её частей данные по отдельным единицам совокупности подвергают сводке и получают обобщающие показатели, как результаты познания количественной стороны явлений. Показатели могут быть представлены абсолютными, относительными и средними величинами. Абсолютные показатели получают путем непосредственного измерения характеристик отдельных единиц совокупности (индивидуальные абсолютные показатели), а также путем суммирования первичных данных, характеризующих численность совокупности и объём (размер) изучаемого явления в конкретных границах места и времени (общие абсолютные показатели). Абсолютные показатели в зависимости от способа измерения могут быть: – натуральные (тонна, штука, квадратный метр, предприятие, человек и т.д.); – условно-натуральные (тонна условного топлива, условная мощность, условная консервная банка, условное содержание действующего начала или основного потребительского свойства в продукции и т.д.); – стоимостные (денежные). Абсолютная величина в статистике есть форма количественного выражения статистических показателей, непосредственно характеризующая размеры социально-экономических явлений, их признаков в единицах меры протяжённости, площади, массы, стоимости и т.п., в единицах счёта времени, в денежных единицах или в виде числа элементов (единиц), составляющих данное массовое явление, изучаемое статистикой и называемое совокупностью статистической. Различают следующие абсолютные величины: Индивидуальные, относящиеся к отдельным единицам совокупности; Групповые и общие, отображающие размеры признака или число единиц соответственно в отдельных частях совокупности или в совокупности в целом. Индивидуальные абсолютные величины получаются в процессе статистического наблюдения. Групповые и общие абсолютные величины образуются в процессе обработки материалов наблюдения, обобщения (обычно суммирования) абсолютных размеров признака у отдельных единиц совокупности или в результате подсчёта числа единиц совокупности, входящих в отдельные группы, или всей совокупности в целом. Они используются в планировании, учёте, анализе, управлении. С помощью абсолютных величин характеризуется, большинство экономических показателей: производство основных видов продукции, величина капитальных вложений, численность занятых в производственном процессе трудовых ресурсов, сумма товарооборота, величина национального дохода и т.д. явления, выявления определённых закономерностей, разносторонней характеристики изучаемого явления приходится прибегать к сопоставлению относительных и средних величин. , 7. Относительные величины, их виды, область практического применения в изучении экономических явлений. Относительные величины получают путём сопоставления различных величин, представляют собой частное от деления двух статистических величин и характеризуют количественное соотношение между ними. Сопоставлять можно одноименные (одной размерности) показатели, относящиеся к различным периодам времени, различным объектам или разным территориям. Результат такого сопоставления может быть представлен коэффициентом или выражен в процентах и показывает, во сколько раз или на сколько процентов сравниваемый показатель больше или меньше базисного. В результате сопоставления показателей получают следующие виды относительных величин: – относительные величины динамики; – относительные величины выполнения плана и планового задания; – относительные величины структуры; – относительные величины координации; – относительные величины наглядности; – относительные величины интенсивности. Относительная величина динамики характеризует изменение изучаемого явления во времени, выявляет направление развития, т.е. показывает, во сколько раз увеличился (или уменьшился) уровень показателя по сравнению с базисным периодом времени. В планах предприятия задания устанавливаются как в абсолютных, так и в относительных показателях. Относительная величина планового задания показывает, во сколько раз или на сколько процентов должна увеличиться (или уменьшиться) величина показателя по плану в сравнении с его уровнем в базисном периоде. Относительная величина выполнения плана показывает, во сколько раз фактический уровень показателя в отчётном периоде больше или меньше планового уровня показателя в том же периоде. Относительные величины планового задания, выполнения плана и динамики связаны между собой. Обозначим:
т.е. относительная величина динамики может быть получена произведением относительных величин планового задания и выполнения плана. Относительные величины структуры характеризуют долю отдельных частей в общем объёме совокупности и рассчитываются как отношение объёма признака в отдельных частях совокупности к общему объёму по всей совокупности. Например, доля мужского и женского населения страны, доля городского и сельского населения. Относительные величины координации применяются для характеристики соотношения между отдельными частями статистической совокупности, причём одна из частей целого выбирается в качестве базовой величины сравнения. Примерами могут быть соотношения между численностью рабочих и служащих, численностью мужского и женского населения, между величиной заёмного и собственного капитала предприятия. Относительные величины наглядности отражают результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду, но к разным объектам или территориям. Этот вид величин применяется для сравнительной оценки уровня развития стран, регионов, отдельных предприятий, для сопоставления цен на продукцию различных предприятий, средней заработной платы этих предприятий и т.д. Относительными величинами интенсивности называют отношения между разноименными абсолютными величинами. Эти величины показывают, насколько широко распространено явление в определенной среде. Относительные величины интенсивности всегда поименованы. Например, показатели инфраструктуры, доходов и естественного движения населения (количество магазинов на 10000 жителей, валовой внутренний продукт в рублях на душу населения, число родившихся на 1000 жителей) и показатели технической оснащенности и эффективности труда (электрическая мощность на 1 рабочего, фондовооружённость в рублях на одного работника, производительность труда в единицах измерения продукции за единицу времени на одного работника). , 8. Понятие средних величин, их виды и условия применения. Средние величины – это обобщающие показатели общественных явлений по одному количественно варьирующему признаку. Ср. выражает типичное единиц совокупности. Особенности ср.: 1) она характеризует ту или иную совокупность в целом; 2) в ней ср. погашаются отдельные индивидуальные отклонения единиц по изучаемому признаку; 3) ср. отражает типичные черты и свойства массы единиц; 4) в сочетании с методом статистических группировок возникает возможность изучения взаимосвязей между группировочными и результативными признаками; 5) ср. величина является базой для прогнозирования; 6) многие процессы изучаются только на основании ср.; 7) ср. показывает количественное различие и сходство двух совокупностей. При расчете ср.: 1) расчет только однородных по качеству совокупностей, для этого надо сочетать метод ср. и метод группировок2) общее ср. необходимо дополнять групповыми средними и индивидуальными величинами3) для расчета ср. нужна масса единиц4)необходимо правильно выбирать единицу совокупности ср.В каждом конкретном случае применяется одна из ср. величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д. Все они - класс степенных средних и объединяются общей формулой (при различных значениях m): В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется ср. гармоническая простая. Ср. геометрическая: применяется, когда характеризуют средний коэффициент роста.Она исчисляется извлечением корня степени п из произведения отдельных значений. Широко применяется для определения средних темпов изменения в рядах динамики, а также в рядах распределения. Ср. квадратическая: применяется, когда нужен расчет среднего размера признака, выраженного в квадратных единицах измерения. Она бывает простой, средней, кубической, кубической (простой, взвешенной). Особым видом средних величин являются структурные ср. К таким показателям относятся мода и медиана. Мода Мо – значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту. Модальный интервал определяется по наибольшей частоте. Медиана Ме – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные части – меньше медианы и больше медианы. Необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В случае четного объема ряда медиана равна средней из двух вариантов. Значение медианы вычисляется линейной интерполяцией по формуле:
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.221 (0.011 с.) |

 - фактический уровень показателя в базисном периоде;
- фактический уровень показателя в базисном периоде; 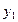 – фактический уровень в отчётном периоде;
– фактический уровень в отчётном периоде;  – планируемый уровень на отчётный период. Тогда: относительная величина планового задания –
– планируемый уровень на отчётный период. Тогда: относительная величина планового задания – 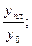 относительная величина выполнения плана –
относительная величина выполнения плана –  относительная величина динамики –
относительная величина динамики –  Справедлива связь
Справедлива связь 
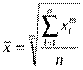 . Различают следующие виды степенных средних: 1) m = -1 – гармоническая
. Различают следующие виды степенных средних: 1) m = -1 – гармоническая  ; 2) m = 0 – геометрическая
; 2) m = 0 – геометрическая 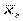 ; 3) m = 1 – арифметическая
; 3) m = 1 – арифметическая  ; 4) m = 2 – квадратическая
; 4) m = 2 – квадратическая 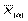 ; 5) m = 3 – ср. кубическая
; 5) m = 3 – ср. кубическая 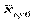 . Ср. арифметическая: наиболее распространенный вид средних. Ср. арифметическая применяется в форме простой ср. и взвешенной ср. 9. Методика расчёта средних степенных (простых и взвешенных) и область их практического применения Ср. арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений. Ср. арифметическая взвешенная – ср. сгруппированных величин х1,х2,…,хп – вычисляется по формуле:
. Ср. арифметическая: наиболее распространенный вид средних. Ср. арифметическая применяется в форме простой ср. и взвешенной ср. 9. Методика расчёта средних степенных (простых и взвешенных) и область их практического применения Ср. арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений. Ср. арифметическая взвешенная – ср. сгруппированных величин х1,х2,…,хп – вычисляется по формуле:  . В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (% или доли единиц). Тогда формула ср. арифметической взвешенной будет иметь вид:
. В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (% или доли единиц). Тогда формула ср. арифметической взвешенной будет иметь вид:  , где
, где  - частость, т.е. доля каждой частоты в общей сумме всех частот. Если частоты подсчитываются в долях (коэффициентах), то
- частость, т.е. доля каждой частоты в общей сумме всех частот. Если частоты подсчитываются в долях (коэффициентах), то  и формула средней арифметической взвешенной имеет вид:
и формула средней арифметической взвешенной имеет вид:  . Ср. гармоническая: когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение
. Ср. гармоническая: когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение  , применяется формула ср. гармонической взвешенной:.
, применяется формула ср. гармонической взвешенной:. 
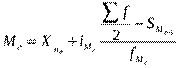 .
.


