
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный и регрессионный методы в анализе взаимосвязи экономических явлений
, Массовые явления и процессы социально-экономической жизни тесно взаимосвязаны между собой и взаимозависимы. Показатели, характеризующие эти явления и процессы, как правило, составляют единую систему и могут быть связаны корреляционными зависимостями различной степени тесноты, которые исследуются в статистике с помощью методов корреляционного и регрессивного анализа. Корреляционный анализ взаимосвязи показателей позволяет решать следующие задачи: 1. Оценка тесноты связи между показателями с помощью парных и множественных коэффициентов корреляции. 2. Оценка уравнения регрессии. Цель регрессионного анализа – получение оценки функциональной зависимости теоретического среднего значения результативного признака Статистическая модель взаимосвязи явлений в виде уравнения регрессии
будет адекватно описывать реальное явление или процесс при выполнении следующих основных условий: 1) результативный признак должен подчиняться нормальному закону распределения относительно своих средних значений при различных значениях факторных признаков; 2) отдельные наблюдения, на основе которых строится модель регрессии, должны быть получены независимо друг от друга. Одной из проблем построения уравнения регрессии является выбор её размерности –определение числа факторов, включаемых в модель. Число факторных признаков, входящих в модель должно быть оптимальным, т.е. необходимо учитывать существенные признаки и исключать несущественные (второстепенные). Корреляционно-регрессионные модели, какими бы сложными они не были, не вскрывают полностью всех причинно-следственных связей, однако достаточно адекватно могут описывать влияние на результативные признаки существенных факторов, если проведён предварительный качественный анализ сущности и специфики исследуемых явлений и процессов. В теории статистики изучаются парные и множественные корреляции. В парной корреляции рассматривается связь результативного признака с одним единственным факторным признаком, во множественной – с двумя и более факторными признаками. В соответствии с этим строящиеся регрессионные модели могут быть парные и множественные.
Например, если устанавливается зависимость уровня оплаты труда Парная регрессия, характеризующая связь между результативным и факторным признаками, аналитически описывается уравнениями различного типа:
прямая
гипербола
парабола
показательная функция
степенная функция
полулогарифмическая функция
Определить тип уравнения можно, используя различные способы, например, исследуя зависимость между признаками графически. Оценка параметров
Распространенным случаем связи в общественных и экономических явлениях является прямая зависимость между результативным и факторным признаком. Для прямой зависимости
Минимизируя
Преобразовав уравнения, получим систему обычных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов:
Решая систему этих уравнений, находим:
где – число единиц наблюдений (пар значений Используя алгоритм, аналогичный рассмотренному выше, можно определить параметры парной регрессии, описываемой другими видами уравнений – гиперболой, параболой и др. 30. Определение тесноты связи признаков экономических явлений. Измерение тесноты и направления связи между признаками предлагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторов.
Линейный коэффициент корреляции был впервые введен в начале 90-х гг. 19 века Пирсоном, Эджвортом и Велдоном и характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. В расчете этого коэффициента учитывается величина отклонений индивидуальных значений признаков от средней величины:
Для получения обобщающей характеристики тесноты связи берут среднее произведение нормированных отклонений:
Формула линейного коэффициента корреляции может быть представлена в следующем виде:
Используя математические свойства средней, получаем:
Преобразования данной формулы позволяют получить следующую формулу линейного коэффициента корреляции:
где n - число наблюдений Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
или
Коэффициент корреляции может быть выражен через дисперсии слагаемых:
Формулы (1), (2), (2) применяются при изучении совокупностей малого объема (n<=20:30). Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой: для парной корреляции - для многофакторной корреляции - Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределение которых близко к нормальному. Линейный коэффициент корреляции изменяется в пределах от -1 до 1. При этом оценку линейного коэффициента корреляции можно представить в таблице:
По степени тесноты связи различают количественные критерии оценки тесноты связи на основе шкалы Чеддока:
В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда δ2 характеризует отклонения групповых средних результативного показателя от общей средней:
где η - корреляционное отношение; σ2 - общая дисперсия
Теоретическое корреляционное отношение определяется по формуле:
где σ2 - дисперсия эмпирических (фактических) значений результативного признака. Так как
Тогда В основе расчета корреляционного отношения лежит правило сложения дисперсий, при этом средняя из межгрупповых дисперсий отражает вариацию результативного признака У под влиянием всех неучтенных при анализе факторов, т.е. носит остаточный характер. Поэтому её часто называют остаточной дисперсией.
Отсюда формула корреляционного отношения принимает вид (выражаем межгрупповую дисперсию через общую и среднюю из внутригрупповых):
Корреляционное отношение изменяется в пределах от 0 до 1 и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции. Теоретическое корреляционное отношение также может выражаться по формуле:
Корреляционное отношение является более универсальным показателем тесноты связи сравнению с линейным коэффициентом корреляции. Для измерения тесноты связи при множественной корреляционной зависимости, т.е. при исследовании трех и более признаков одновременно, вычисляются множественный или совокупный и частные коэффициенты корреляции. Множественный коэффициент корреляции рассчитывается при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков. В случае оценки связи между результативным (У) и двумя факторными признаками (х1 и х2) множественный коэффициент корреляции определяют по формуле:
где r - парные коэффициенты корреляции между признаками Множественный коэффициент корреляции можно рассчитать, используя парные коэффициенты rij и коэффициенты регрессии в стандартизованном масштабе (βi)
где ryxi - парные коэффициенты; βi - коэффициенты в стандартизованном масштабе. Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен. Приближение R к 1 свидетельствует о сильной зависимости между признаками. Чтобы оценить общую вариацию результативного признака в зависимости от факторных признаков, величина коэффициента множественной корреляции корректируется на основании следующего выражения:
где n- число наблюдений; k - число факторных признаков. Корректировка не производится при условии, если
Проверка значимости коэффициента множественной корреляции осуществляется на основании F-критерия Фишера-Снедекора
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками х1 и х2 при фиксированном значении других (к‑2) факторных признаков, т.е. когда влияние х3 и других исключается и оценивается связь между х1 и х2 в "чистом виде". Коэффициент, в котором исключается влияние только одного факторного признака, называется коэффициентом частной корреляции первого порядка. В общем виде коэффициент корреляции первого порядка выражается так:
В случае зависимости Y от двух факторных признаков х1 и х2 коэффициент частной корреляции следующий:
В первом случае исключено влияние факторного признака х2, во втором - х1. Значения парного и частного коэффициентов корреляции отличаются друг от друга, так как парный коэффициент характеризует связь между двумя признаками без учета влияния других признаков, а частный учитывает наличие и влияние других факторов. Кроме перечисленных выше коэффициентов для измерения тесноты применяются коэффициент детерминации. Он равен квадрату корреляционного отношения и обозначается буквой η2 В числителе формулы стоит сумма квадратов отклонений фактических значений признака у от индивидуальных расчетных показателей. Эта сумма не может равняться нулю, если связь не является функциональной. При неверной формуле или ошибки в расчетах возрастают расхождения фактических и расчетных значений, и корреляционное отношение снижается. С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности, определяемые по формуле:
где
аi - коэффициент регрессии при соответствующем факторном признаке. Коэффициент эластичности показывает, на сколько в среднем изменится значение результативного признака при изменении факторного признака на 1%. Частный коэффициент детерминации показывает на сколько процентов вариация результативного признака объясняется вариацией i-того признака, входящего в множественное уравнение регрессии и определяется по формуле:
где ryxi - парный коэффициент корреляции между результативным и i-м факторным признаками; βхi - соответствующий коэффициент уравнения множественной регрессии в стандартизованном виде. Множественный коэффициент детерминации (R2) представляет собой множественный коэффициент корреляции в квадрате и показывает какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель. Для более точной оценки влияния каждого факторного признака на моделируемый используют Q-коэффициент, определяемый по формуле:
где Интерпретировать корреляционные показатели строго следует лишь в терминах вариации отклонений от средней величины. Если же необходимо измерение изменений признака во времени, то метод корреляционно-регрессионного анализа требует значительного изменения. Модели на основе этого метода обладают слабыми экстраполяционными свойствами и не отражают тенденции развития и пригодны лишь для построения краткосрочных прогнозов. Б
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.186.218 (0.045 с.) |
 от факторных
от факторных  . При этом в регрессионном анализе заранее предполагается наличие причинно-следственных связей между результативным и факторными признаками.
. При этом в регрессионном анализе заранее предполагается наличие причинно-следственных связей между результативным и факторными признаками.
 от производительности труда
от производительности труда  то такая регрессия парная. Если же изучается зависимость уровня оплаты труда
то такая регрессия парная. Если же изучается зависимость уровня оплаты труда  но и от квалификации работников
но и от квалификации работников  цены продукции
цены продукции  качества продукции
качества продукции  то такая регрессия множественная.
то такая регрессия множественная.




 и др.
и др. уравнений регрессии осуществляется методом наименьших квадратов, сущность которого состоит в нахождении параметров регрессии
уравнений регрессии осуществляется методом наименьших квадратов, сущность которого состоит в нахождении параметров регрессии  при которых сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по уравнению регрессии, минимальна. Т.е.
при которых сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по уравнению регрессии, минимальна. Т.е.
 .
. как функцию параметров
как функцию параметров  и
и  , получаем систему уравнений:
, получаем систему уравнений:




 ).
). и
и  . Однако, сопоставляемые полученные величины могут быть выражены в различных единицах измерения или могут различны по величине. Поэтому сравнивают нормированные отклонения:
. Однако, сопоставляемые полученные величины могут быть выражены в различных единицах измерения или могут различны по величине. Поэтому сравнивают нормированные отклонения: и
и 
 (1)
(1)
 (2)
(2) или
или  (3)
(3) (4)
(4) (5)
(5) (6)
(6) или
или  , а коэффициент
, а коэффициент 
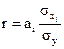 где аi - коэффициент регрессии в уравнении связи, σхi - среднее квадратическое отклонение соответствующего, статистически существенного, факторного признака.
где аi - коэффициент регрессии в уравнении связи, σхi - среднее квадратическое отклонение соответствующего, статистически существенного, факторного признака. (7)
(7) - средняя из частных (внутригрупповых) дисперсий;
- средняя из частных (внутригрупповых) дисперсий; - межгрупповая дисперсия (дисперсия групповых средних)
- межгрупповая дисперсия (дисперсия групповых средних) (8)
(8) - дисперсия выровненных значений результативного признака, т.е. рассчитанных по уравнению регрессии;
- дисперсия выровненных значений результативного признака, т.е. рассчитанных по уравнению регрессии; и
и 
 (9)
(9)
 (10)
(10)
 (11)
(11)

 - скорректированное значение;
- скорректированное значение;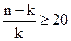





 - среднее значение соответствующего факторного признака;
- среднее значение соответствующего факторного признака; - среднее значение результативного признака;
- среднее значение результативного признака;

 - коэффициент вариации соответствующего факторного признака.
- коэффициент вариации соответствующего факторного признака.


