
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические показатели вариации признаков и их экономический смысл.
Вариация- различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. К показателям вариации относятся: размах вариации,среднее линейное отклонение,дисперсия,среднее квадратическое отклонение, коэффициент вариации. размах вариации R,
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.184.90 (0.003 с.) |
 .Размах вариации показывает лишь крайние отклонения признака. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику. Это среднее линейное отклонение
.Размах вариации показывает лишь крайние отклонения признака. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику. Это среднее линейное отклонение  ( среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической). Среднее линейное отклонение для несгруппированных данных:
( среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической). Среднее линейное отклонение для несгруппированных данных: 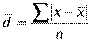 , где п – число членов ряда; для сгруппированных данных:
, где п – число членов ряда; для сгруппированных данных:  , где
, где  - сумма частот вариационного ряда. Дисперсия признака - средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий. Простая дисперсия для несгруппированных данных:
- сумма частот вариационного ряда. Дисперсия признака - средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий. Простая дисперсия для несгруппированных данных:  ; взвешенная дисперсия для вариационного ряда:
; взвешенная дисперсия для вариационного ряда: 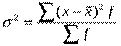 .Cвойства дисперсии: 1) если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, дисперсия не изменится; 2) если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия уменьшится или увеличится в
.Cвойства дисперсии: 1) если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, дисперсия не изменится; 2) если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия уменьшится или увеличится в 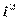 раз. Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
раз. Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:  , где i – величина интервала;
, где i – величина интервала;  -новые (преобразованные) значения вариантов (А – условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);
-новые (преобразованные) значения вариантов (А – условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);  - момент второго порядка;
- момент второго порядка;  - квадрат момента первого порядка. Среднее квадратическое отклонение
- квадрат момента первого порядка. Среднее квадратическое отклонение 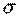 равно корню квадратному из дисперсии: для несгруппированных данных:
равно корню квадратному из дисперсии: для несгруппированных данных:  , для вариационного ряда:
, для вариационного ряда:  . Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Исчисляем среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака
. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Исчисляем среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака  . Дисперсия альтернативного признака:
. Дисперсия альтернативного признака:  . Подставив в формулу дисперсии q = 1 – p, получим
. Подставив в формулу дисперсии q = 1 – p, получим  . Таким образом,
. Таким образом,  - дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих данным признаком. Среднее квадратическое отклонение альтернативного признака
- дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих данным признаком. Среднее квадратическое отклонение альтернативного признака  . Для сравнения вариаций различных признаков, используют относительный показатель вариации – коэффициент вариации. Коэффициент вариации отношение среднего квадратического отклонения к средней арифметической:
. Для сравнения вариаций различных признаков, используют относительный показатель вариации – коэффициент вариации. Коэффициент вариации отношение среднего квадратического отклонения к средней арифметической:  . Также коэффициент вариации используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%
. Также коэффициент вариации используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%


