
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы инерции во вращающейся системе отсчетаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим теперь поведение тел в неинерциальной системе отсчета, вращающейся относительно инерциальной системы с постоянной угловой скоростью. Такой системой, например, может быть диск, вращающийся вокруг перпендикулярной к нему оси с угловой скоростью Допустим, что по окружности радиуса
Знак в этой формуле зависит от направления движения шарика. Ускорение шарика в неподвижной системе определяется выражением
где В полученном выражении величина
Таким образом, во вращающейся неинерциальной системе
называется центробежной силой инерции. Эта сила направлена вдоль радиуса от оси вращения. Она действует во вращающихся системах отсчета на все тела, независимо от того, покоится тело в этих системах отсчета или движется. Вторая сила, называемая силой Кориолиса, в векторной форме может быть представлена в виде
Действительно, модуль векторного произведения На основании анализа формулы (6.8) можно сделать следующие выводы: - сила Кориолиса действует только на движущиеся тела во вращающейся системе отсчета; - сила Кориолиса перпендикулярна вектору - сила Кориолиса перпендикулярна вектору скорости Любая система отсчета, связанная с Землей, является неинерциальной системой. Вращение Земли приводит к действию как центробежной, так и кориолисовой сил. Векторная сумма силы гравитационного притяжения Земли и центробежной силы инерции рассматривается как единая величина, называемая силой тяжести
Более существенно влияет на характер движения тел кориолисова сила. Так, при свободном падении тел происходит их отклонение к востоку от линии подвеса. Этот эффект максимален на экваторе и отсутствует на полюсе. Для широты Москвы при падении с высоты 100 м это отклонение составляет 1,2 см. Действие силы Кориолиса приводит также к отклонению движущихся вдоль меридиана тел к востоку в северном полушарии и к западу в южном. Именно этим объясняется то, что реки северного полушария, текущие в меридианальном направлении, подмывают всегда правый берег. Примеры решения задач
Решение На тело, находящееся на вращающемся диске и движущееся относительно него с постоянной скоростью, действуют центробежная сила инерции и сила Кориолиса. Центробежная сила инерции направлена вдоль радиуса и равна
Сила Кориолиса, как это следует из ее векторного выражения, перпендикулярна скорости движения тела и направлена к нам (рис.6.4). Величина этой силы равна
Таким образом, равнодействующая этих двух взаимно перпендикулярных сил определяется по теореме Пифагора
2. Тело массой m =1кг, падая свободно в течение τ =6с, попадает на Землю в точку с географической широтой φ=600. Учитывая вращение Земли, а) показать и определить все силы, действующие на тело в момент падения; б) определить отклонение тела при его падении от вертикали. Решение
Сила тяготения направлена к центру Земли и равна
где
Центробежная сила инерции направлена вдоль радиуса от оси вращения. Величина этой силы определяется по формуле
где После подстановки, получим
Сила Кориолиса направлена на восток и равна
где В момент падения
Для определения отклонения тела при его падении от вертикали учтем, что сила Кориолиса сообщает ускорение
За время падения t горизонтальная составляющая скорости, направленная к востоку,будет равна
В результате за время τ тело сместится к востоку по горизонтали на расстояние
Проведенные вычисления дают следующие результаты: s=2,56 см.
Основные положения 1. Уравнение динамики в неинерциальной системе отсчета, движущейся поступательно с ускорением
где 2. Принцип эквивалентности – движение тела по отношению к неинерциальной системы отсчета эквивалентно его движению относительно инерциальной системы, совершающемуся под влияние всех реально взаимодействующих с ним тел, а также некоторого дополнительного поля тяготения. 3. Силы инерции во вращающейся системе отсчета: - центробежная сила - сила Кориолиса Контрольные вопросы 1. Какие системы отсчета являются неинерциальными? Как формулируется уравнение динамики в неинерциальных системах отсчета? 2. Как определяется сила инерции при ускоренном поступательном движении системы отсчета? 3. В чем заключается принцип эквивалентности сил инерции и тяготения? 4. Чему равны и как направлены центробежная сила инерции и сила Кориолиса во вращающейся системе отсчета? 5. Приведите примеры действия сил Кориолиса в земных условиях. Механика упругих тел
Все реальные тела деформируются. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями.Различают два предельных случая: деформации упругие и деформации пластические. Упругиминазываются деформации, исчезающие после прекращения действия приложенных сил. Пластическими деформациями называются такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия приложенных сил. Ограничимся изучением только упругих деформаций, считая тела идеально упругими. Такая идеализация возможна лишь для очень малых деформаций. Для них существует линейная зависимость между действующими силами и вызывающими ими деформациями, подчиняющимися закону Гука. Любая сложная деформация твердого тела может быть представлена как результат наложения более простых деформаций. Рассмотрим основные виды деформаций: одноосное растяжение (сжатие); сдвиг; кручение.
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.89.89 (0.007 с.) |

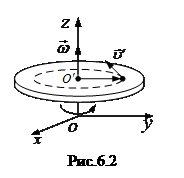
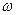 (рис.6.2).
(рис.6.2).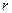 равномерно движется, привязанный нитью к оси диска, шарик со скоростью
равномерно движется, привязанный нитью к оси диска, шарик со скоростью 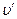 относительно диска, т.е. неинерциальной системы отсчета. Скорость шарика относительно инерциальной системы будет равна
относительно диска, т.е. неинерциальной системы отсчета. Скорость шарика относительно инерциальной системы будет равна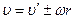 . (6.5)
. (6.5)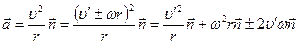 ,
,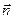 - единичный вектор, направленный к центру окружности.
- единичный вектор, направленный к центру окружности. представляет собой ускорение шарика относительно диска, т.е. вращающейся системы
представляет собой ускорение шарика относительно диска, т.е. вращающейся системы 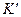 , а произведение
, а произведение 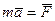 дает силу натяжения нити. Следовательно, основной закон динамики во вращающейся системе отсчета можно написать следующим образом
дает силу натяжения нити. Следовательно, основной закон динамики во вращающейся системе отсчета можно написать следующим образом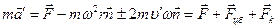 . (6.6)
. (6.6)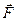 , обусловленной натяжением нити, действуют еще две дополнительные силы. Первая из них, определяемая выражением
, обусловленной натяжением нити, действуют еще две дополнительные силы. Первая из них, определяемая выражением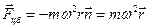 , (6.7)
, (6.7)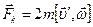 . (6.8)
. (6.8) равен
равен 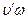 , так как угол между данными векторами равен
, так как угол между данными векторами равен 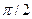 , а его направление совпадает или противоположно с
, а его направление совпадает или противоположно с 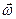 , поэтому всегда лежит в плоскости, перпендикулярной оси вращения;
, поэтому всегда лежит в плоскости, перпендикулярной оси вращения;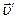 и не совершает работы над движущимся телом; эта сила может изменить только направление скорости, но не ее модуль.
и не совершает работы над движущимся телом; эта сила может изменить только направление скорости, но не ее модуль.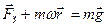 . (6.9)
. (6.9)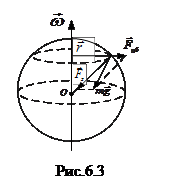 Направление этой силы определяется диагональю параллелограмма, построенного на векторах
Направление этой силы определяется диагональю параллелограмма, построенного на векторах 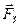 и
и  (рис.6.3). Таким образом, направление к центру Земли не совпадает с направлением отвеса, хотя ввиду медленности вращения Земли оба направления отличаются друг от друга незначительно.
(рис.6.3). Таким образом, направление к центру Земли не совпадает с направлением отвеса, хотя ввиду медленности вращения Земли оба направления отличаются друг от друга незначительно. 1. Горизонтальный диск вращается с постоянной угловой скоростью ω= 6 рад/с вокруг вертикальной оси, проходящей через его центр. По одному из диаметров диска движется небольшое тело массой m =0,5 кг с постоянной относительно диска скоростью
1. Горизонтальный диск вращается с постоянной угловой скоростью ω= 6 рад/с вокруг вертикальной оси, проходящей через его центр. По одному из диаметров диска движется небольшое тело массой m =0,5 кг с постоянной относительно диска скоростью 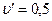 м/с. Какая сила действует на это тело в момент, когда оно находится на расстоянии r =0,3 м от оси вращения.
м/с. Какая сила действует на это тело в момент, когда оно находится на расстоянии r =0,3 м от оси вращения.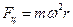 .
.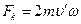 .
.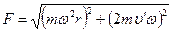 .
. Все силы, действующие на тело в момент падения, показаны на рис.6.5.
Все силы, действующие на тело в момент падения, показаны на рис.6.5.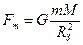 ,
,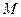 ,
,  - масса и радиус Земли.
- масса и радиус Земли. ,
, 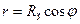 .
.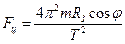 .
.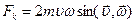 ,
,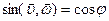 .
.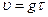 , поэтому
, поэтому .
. .
.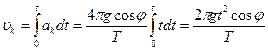 .
. .
.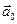 относительно инерциальной системы, имеет вид
относительно инерциальной системы, имеет вид ,
,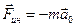 - поступательная сила инерции.
- поступательная сила инерции. ;
;


