
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание положения материальной точкиСтр 1 из 23Следующая ⇒
В пространстве
Положение точки М относительно этой системы координат будет однозначно определено, если будут заданы ее координаты x, y и z. Вместо трех скалярных величин положение точки может быть задано одной векторной -
Модуль вектора равен
При движении материальной точки ее положение относительно выбранной системы отсчета, а следовательно, ее радиус-вектор и координаты с течением времени изменяются. Поэтому в общем случае ее движение будет однозначно определено заданием трех скалярных уравнений
либо эквивалентного им одного векторного уравнения
Эти уравнения называются кинематическими уравнениями движения материальной точки. Решая уравнения (1.3) совместно и исключая параметр t, можно получить уравнение траектории движения материальной точки, т.е. линии, вдоль которой перемещается конец радиус-вектора. В зависимости от формы траектории различают прямолинейное и криволинейное движение точки. При одномерном движении траектория представляет собой прямую линию, определяемую осью координат. Если траектория точки целиком лежит в одной плоскости, то движение называют плоским (двумерным). В общем случае траектория точки представляет собой пространственную кривую. Например, пусть кинематические уравнения движения заданы в форме
где Решение данной системы уравнений дает уравнение траектории точки
т.е. точка движется в плоскости z =0 по эллиптической траектории.
Итак, мы можем сказать, что положение материальной точки полностью определяется векторной величиной
Скорость
Для характеристики направления и быстроты движения материальной точки вводится понятие скорости. Введем вначале понятие вектора средней скорости. Отношение вектора перемещения
Вектор
Таким образом, вектор скорости материальной точки в данный момент времени есть первая производная ее радиус-вектора по времени. Вектор скорости в любой точке траектории направлен по касательной к траектории точки в сторону ее движения. Модуль вектора скорости равен
т.е. величина скорости в данный момент времени равна производной пути по времени. Вектор скорости, как и всякий другой вектор, можно разложить на его составляющие по осям координат
С другой стороны
Из сравнения (1.6) и (1.7) следует, что
т.е. проекции вектора скорости на координатные оси равны производным по времени соответствующих координат точки. При этом численное значение скорости можно представить также в виде
В соответствии с экспериментальным принципом независимости движений, если точка одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых за то же время в каждом из движений порознь. Такой же вывод можно сделать и для скорости движения, получивший название закона сложения скоростей
где Таким образом, при трехмерном (или двухмерном) движении мы можем рассматривать перемещение и скорость точки в направлении любой оси координат независимо от того, как она движется относительно других осей.
Ускорение
При движении точки по криволинейной траектории величина и направление скорости могут изменяться. Быстроту изменения вектора скорости с течением времени характеризует ускорение. Рассмотрим движение материальной точки по некоторой кривой (1.3). Пусть в некоторый момент времени t1 точка имела скорость
Мгновенным ускорением или ускорением точки в данный момент времени t называют величину, математически определяемую как
Таким образом, вектор ускорения в любой момент времени равен первой производной по времени от вектора скорости, или второй производной от радиус-вектора. Численное значение ускорения можно рассчитать через вторую производную от пути по времени
Вектор ускорения можно представить в виде векторной суммы его составляющих по осям координат
В то же время, дифференцируя вектор скорости по времени, получаем
Из сопоставления (1.15) и (1.16) следует, что проекции вектора ускорения на координатные оси равны первым производным соответствующих проекций скорости или вторым производным соответствующих координат по времени. Величина ускорения в этом случае равна
При построении мы отложили отрезок АС=АD, в результате чего, вектор
Разделив обе части выражения (1.18) на
Первое слагаемое в правой части представляет ускорение, которое характеризует только изменение скорости по величине, оно называется тангенциальным ускорением. Второе слагаемое характеризует только изменение направления скорости и называется нормальным ускорением. Можно показать, что
где
где Таким образом, тангенциальное и нормальное ускорения представляют собой две взаимно перпендикулярные составляющие полного ускорения, а следовательно,
|
|||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.107.90 (0.016 с.) |
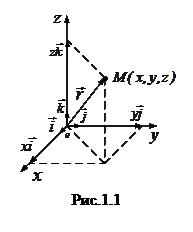 Любое механическое движение относительно. Поэтому, для определения положения материальной точки в пространстве и аналитического описания ее движения необходимо выбрать систему отсчета. Система отсчета представляет собой систему координат, снабженную часами и жестко связанную с телом отсчета, по отношению к которому определяется положение других тел в различные моменты времени. Наиболее часто используется правая прямоугольная декартовая система координат, в которой ориентация орт
Любое механическое движение относительно. Поэтому, для определения положения материальной точки в пространстве и аналитического описания ее движения необходимо выбрать систему отсчета. Система отсчета представляет собой систему координат, снабженную часами и жестко связанную с телом отсчета, по отношению к которому определяется положение других тел в различные моменты времени. Наиболее часто используется правая прямоугольная декартовая система координат, в которой ориентация орт  и
и  совпадает с взаимной ориентацией трех пальцев правой руки – большого, указательного и среднего, когда они расположены взаимно перпендикулярно (рис.1.1).
совпадает с взаимной ориентацией трех пальцев правой руки – большого, указательного и среднего, когда они расположены взаимно перпендикулярно (рис.1.1). , радиус-вектором, проведенным из начала координат в точку М. Координаты x, y и z являются проекциями радиус-вектора на координатные оси
, радиус-вектором, проведенным из начала координат в точку М. Координаты x, y и z являются проекциями радиус-вектора на координатные оси . (1.1)
. (1.1) . (1.2)
. (1.2) (1.3)
(1.3)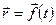 . (1.4)
. (1.4) ,
, .
. ,
,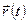 и основной задачей кинематики точки является нахождение закономерностей, определяющих ее изменение со временем.
и основной задачей кинематики точки является нахождение закономерностей, определяющих ее изменение со временем. Рассмотрим движение точки по произвольной криволинейной траектории (рис.1.2). Пусть в момент времени t1 она занимала положение А, определяемое радиус-вектором
Рассмотрим движение точки по произвольной криволинейной траектории (рис.1.2). Пусть в момент времени t1 она занимала положение А, определяемое радиус-вектором  , а в момент времени t2 – положение В, определяемое радиус-вектором
, а в момент времени t2 – положение В, определяемое радиус-вектором  . Вектор
. Вектор  , проведенный из начальной точки А в конечную В, характеризует изменение пространственного положения точки за данный промежуток времени
, проведенный из начальной точки А в конечную В, характеризует изменение пространственного положения точки за данный промежуток времени  и называется вектором перемещения. Отрезок траектории
и называется вектором перемещения. Отрезок траектории 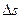 , заключенный между точками А и В, называется путем, пройденным за тот же промежуток времени
, заключенный между точками А и В, называется путем, пройденным за тот же промежуток времени  . В общем случае путь
. В общем случае путь  , однако это различие будет тем меньше, чем меньше
, однако это различие будет тем меньше, чем меньше  , т.е. для бесконечно малого перемещения справедливо равенство
, т.е. для бесконечно малого перемещения справедливо равенство 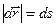 .
. за некоторый интервал времени
за некоторый интервал времени  . (1.4΄)
. (1.4΄) направлен так же, как
направлен так же, как 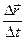 практически перестанет изменяться как по величине, так и по направлению. Это означает, что при
практически перестанет изменяться как по величине, так и по направлению. Это означает, что при  отношение (1.4΄) стремится к некоторому пределу, определяющему вектор скорости в момент времени t:
отношение (1.4΄) стремится к некоторому пределу, определяющему вектор скорости в момент времени t: . (1.5)
. (1.5)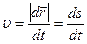 , (1.6)
, (1.6) . (1.7)
. (1.7)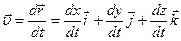 . (1.8)
. (1.8) , (1.9)
, (1.9) . (1.10)
. (1.10)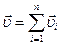 , (1.11)
, (1.11) - скорость материальной точки при i -м независимом движении, n – число таких движений.
- скорость материальной точки при i -м независимом движении, n – число таких движений.
 , а в момент времени t2 - скорость
, а в момент времени t2 - скорость  . Вектор
. Вектор  характеризует изменение скорости за время
характеризует изменение скорости за время  . Отношение изменения скорости
. Отношение изменения скорости  . (1.12)
. (1.12) (1.13)
(1.13) . (1.14)
. (1.14) . (1.15)
. (1.15) . (1.16)
. (1.16) . (1.17)
. (1.17) Вектор ускорения, характеризующий быстроту изменения скорости как по величине, так и по направлению, целесообразно разложить на две составляющие так, чтобы одна из них характеризовала только изменение величины скорости, а другая – только ее направление. С этой целью представим приращение вектора скорости
Вектор ускорения, характеризующий быстроту изменения скорости как по величине, так и по направлению, целесообразно разложить на две составляющие так, чтобы одна из них характеризовала только изменение величины скорости, а другая – только ее направление. С этой целью представим приращение вектора скорости  . (1.18)
. (1.18) характеризует изменение скорости по величине, вектор
характеризует изменение скорости по величине, вектор  - ее изменение по направлению. Проведем также к векторам
- ее изменение по направлению. Проведем также к векторам  . (1.19)
. (1.19) , (1.20)
, (1.20) - единичный вектор, направленный по касательной к траектории в рассматриваемой точке (тангенциальный – означает касательный: отсюда – название ускорения). А также
- единичный вектор, направленный по касательной к траектории в рассматриваемой точке (тангенциальный – означает касательный: отсюда – название ускорения). А также , (1.21)
, (1.21)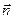 - единичный вектор нормали к мгновенной скорости в рассматриваемой точке траектории, отсюда название – нормальное ускорение; R – радиус кривизны траектории в данной точке.
- единичный вектор нормали к мгновенной скорости в рассматриваемой точке траектории, отсюда название – нормальное ускорение; R – радиус кривизны траектории в данной точке. . (1.22)
. (1.22) На рис.1.5 показаны векторы тангенциального, нормального и полного ускорений для частного случая движения точки А по криволинейной траектории. Направление полного ускорения можно определить углом φ между векторами
На рис.1.5 показаны векторы тангенциального, нормального и полного ускорений для частного случая движения точки А по криволинейной траектории. Направление полного ускорения можно определить углом φ между векторами  и
и  :
: . (1.23)
. (1.23)


