
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения импульса. Система центра масс
Механическую систему называют замкнутой или изолированной, если на нее не действуют внешние силы. Для замкнутой системы главный вектор внешних сил тождественно равен нулю (
Полученное соотношение выражает закон сохранения импульса: векторная сумма импульсов всех тел замкнутой системы в инерциальной системе отсчета не изменяется со временем. Таким образом, импульс механической системы может изменяться под действием только внешних сил, внутренние силы не могут изменить импульс системы. При этом импульсы отдельных тел системы могут испытывать существенные изменения, однако приращение импульса одного тела равно убыли импульса оставшейся части системы. Иными словами, отдельные части системы могут лишь обмениваться импульсами. С учетом выражения, связывающего импульс системы со скоростью ее центра масс ( Закон сохранения импульса относится к фундаментальным (универсальным) законам природы. Он справедлив не только в классической механике, базирующейся на законах Ньютона, но и в квантовой механике, описывающей процессы, происходящие в микромире. Этот закон является следствием определенного физического свойства пространства - его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются. Иначе говоря, изменение выбора начала системы координат не должно отражаться на физических свойствах системы и законах ее движения. В заключении отметим, что в тех случаях, когда нас интересует лишь относительное движение частиц внутри системы, а не ее движение как целого, наиболее целесообразно пользоваться системой отсчета, в которой центр масс покоится. Систему отсчета, жестко связанную с центром масс и перемещающуюся поступательно по отношению к инерциальным системам, называют системой центра масс или С-системой. Отличительной особенностью С-системы является то, что полный импульс системы частиц в ней всегда равен нулю, ибо
Движения тела переменной массы. Формула Циолковского
Имеется много случаев, когда масса тела изменяется в процессе движения за счет непрерывного отделения или присоединения вещества. Типичным примером такой ситуации является реактивное движение, которое осуществляется за счет выброса из сопла ракеты раскаленных газов. Выбрасываемое вещество, в свою очередь, воздействует на ракету и увеличивает ее скорость в противоположном направлении. Рассмотрим задачу о реактивном движении для наиболее простого случая, когда ракета движется в дальнем космосе, так что воздействием на нее Земли и других планет можно пренебречь. Ракета вместе с выброшенным веществом является замкнутой системой. Суммарный импульс такой системы не меняется во времени, и именно закон сохранения импульса лежит в основе решения этой задачи.
где Выполнив преобразования и отбросив член
Для нахождения максимальной скорости ракеты проинтегрируем (3.19), допуская, что начальная скорость ракеты равна нулю, ее стартовая масса равна
Полученное соотношение (3.20) называется формулой Циолковского. Эта формула позволяет рассчитать запас топлива, необходимый для реализации космических полетов на ракетах. Так, при скорости истечения газов 2км/с, для достижения первой космической скорости (
Не представляет особых трудностей обобщение представленного рассмотрения на случай действия внешних сил. В соответствии с законом изменения импульса
Приведем данное выражение к виду
Векторная величина
имеет размерность силы и называется реактивной силой. Она характеризует механическое действие на тело отделяющихся от него или присоединяющихся к нему частиц. Уравнение (3.22) называется уравнением Мещерского и позволяет решать любые задачи механики, связанные с движением тел переменной массы.
Применение законов динамики Среди многообразия различных задач на динамику выделим следующие типы: · На систему действуют постоянные силы. В этом случае по второму закону Ньютона определяется постоянное ускорение, а затем и другие кинематические характеристики. Задачи этого типа сравнительно просты. · Результирующая сила, действующая на тело, не постоянна и зависит от скорости. При решении таких задач требуется интегрирование дифференциального уравнения движения. Задачи второго типа много сложнее первого. · Масса тела непрерывно изменяется из-за потери или приобретения вещества. В этом случае необходимо использовать уравнение Мещерского. Алгоритм решения задач на динамику 1. Сделать чертеж, показав на нем силы, действующие на все тела системы. 2. Написать уравнения движения в векторном виде для каждого из тел системы в отдельности. 3. Выбрать систему координат (для каждого тела системы можно выбирать свою систему) и от векторных уравнений перейти к скалярным, заменяя вектора их проекциями. 4. Решить с учетом конкретных условий задачи систему получившихся скалярных уравнений. Перейдем к рассмотрению конкретных примеров. 1. На горизонтальной поверхности стола лежат два одинаковых бруска массой 1 кг каждый (рис.3.4). Бруски связаны нерастяжимой нитью, такая же нить связывает первый брусок с грузом массой m =0,5 кг. Коэффициент трения первого бруска о стол
Решение
Запишем II закон Ньютона в векторной форме для каждого из тел:
Выбрав оси координат, как показано на рис.3.4 и проектируя векторные выражения на координатные оси х и у, получим:
Учитывая, что
Тогда можно переписать систему уравнений
Решая систему уравнений, и учитывая, что
Решение При движении катера с включенным двигателем на него действуют сила тяги
где, зная связь мощности двигателя и силы тяги, а также учитывая выражение для силы сопротивления, коэффициент сопротивления k можно выразить следующим образом
После выключения двигателя, катер начинает двигаться равнозамедленно под действием силы сопротивления (рис.3.5б). Уравнение движения тела в векторной форме будет иметь вид:
Спроектировав данное уравнение на направление движения, имеем
После разделения переменных получим
Проинтегрируем левую часть уравнения от
Окончательно, для t имеем
После подстановки числовых значений, получим t=17 c. 3. Турбореактивные двигатели самолета выбрасывают из сопел струю газа плотностью ρ = 1,5 кг/м3, с общей площадью поперечного сечения S=0,25 м2 и скоростью u =300 м/с относительно самолета. Определить установившуюся скорость полета самолета Решение Уравнение Мещерского в данной ситуации принимает следующий вид
При установившейся скорости полета поэтому уравнение Мещерского упрощается
Убыль массы газа за время
С учетом этого, получим
4. На горизонтальных рельсах стоит платформа с песком массой m1 =5.103 кг. В песок попадает снаряд массы m2 =5 кг, летевший вдоль рельсов. В момент попадания скорость снаряда Решение
Отсюда Произведя подстановку числовых значений, получим u= 0,34 м/с. 5. Модель ракеты движется при отсутствии внешних сил, выбрасывая непрерывную струю газов с постоянной относительно нее скоростью u =800м/с. Расход газа Решение Для решения этой задачи воспользуемся формулой Циолковского
Масса ракеты к моменту времени t =1c после начала движения будет равна
Подставив полученное значение массы в формулу Циолковского, получим
Расчет по этой формуле дает следующий результат
Основные положения 1. Инерциальная система отсчета – система отсчета, относительно которой тело, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. 2. Динамические характеристики тела при поступательном движении:
3. Основной закон динамики:
|
||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.238.76 (0.054 с.) |
 ), поэтому
), поэтому и
и  (3.17)
(3.17) ), из (3.17) следует, что при любых процессах, происходящих в замкнутой системе, скорость ее центра масс сохраняется (
), из (3.17) следует, что при любых процессах, происходящих в замкнутой системе, скорость ее центра масс сохраняется ( ). Центр масс замкнутой системы либо покоится, либо движется с постоянной скоростью относительно инерциальной системы отсчета.
). Центр масс замкнутой системы либо покоится, либо движется с постоянной скоростью относительно инерциальной системы отсчета. . Любая система частиц как целое покоится в своей С-системе.
. Любая система частиц как целое покоится в своей С-системе. Пусть
Пусть  - масса ракеты в произвольный момент времени
- масса ракеты в произвольный момент времени  ,
,  - ее скорость относительно некоторой инерциальной системы отсчета, а
- ее скорость относительно некоторой инерциальной системы отсчета, а 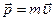 - импульс в тот же момент времени (рис.3.3). По истечении времени
- импульс в тот же момент времени (рис.3.3). По истечении времени  суммарный импульс ракеты и газов, образовавшихся за это время, в соответствии с законом сохранения импульса не изменится, то есть
суммарный импульс ракеты и газов, образовавшихся за это время, в соответствии с законом сохранения импульса не изменится, то есть , (3.18)
, (3.18) - масса образовавшегося газа,
- масса образовавшегося газа,  - скорость истечения газов из ракеты,
- скорость истечения газов из ракеты,  - скорость газа относительно выбранной системы отсчета.
- скорость газа относительно выбранной системы отсчета. , как бесконечно малую высшего порядка, получим
, как бесконечно малую высшего порядка, получим . (3.19)
. (3.19) , а конечная масса -
, а конечная масса - 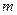 . В результате интегрирования получим
. В результате интегрирования получим . (3.20)
. (3.20) ) необходимо, чтобы отношение начальной массы ракеты к ее конечной было равно 55. Это означает, что почти 98% массы ракеты приходится на топливо. Путь преодоления этой трудности был указан Циолковским. Он впервые обосновал необходимость использования многоступенчатых ракет для достижения космических скоростей.
) необходимо, чтобы отношение начальной массы ракеты к ее конечной было равно 55. Это означает, что почти 98% массы ракеты приходится на топливо. Путь преодоления этой трудности был указан Циолковским. Он впервые обосновал необходимость использования многоступенчатых ракет для достижения космических скоростей. . (3.21)
. (3.21) . (3.22)
. (3.22) (3.23)
(3.23) , второго бруска
, второго бруска  . Найти силу натяжения нити между брусками. Массой блока пренебречь.
. Найти силу натяжения нити между брусками. Массой блока пренебречь. Покажем на рисунке силы действующие на каждое тело системы и направления их ускорений. Так как все тела связаны нерастяжимыми нитями, то модули ускорений будут равны.
Покажем на рисунке силы действующие на каждое тело системы и направления их ускорений. Так как все тела связаны нерастяжимыми нитями, то модули ускорений будут равны. ,
,  ,
, .
.

 .
. ,
,  , находим
, находим ;
;  .
.
 , получим:
, получим:
 2. Катер массой m =2 т с двигателем мощностью N =50 кВт развивает максимальную скорость
2. Катер массой m =2 т с двигателем мощностью N =50 кВт развивает максимальную скорость  м/с. Определить время, в течение которого катер после выключения двигателя потеряет половину своей скорости. Принять, что сила сопротивления движению катера изменяется пропорционально скорости (рис.3.5).
м/с. Определить время, в течение которого катер после выключения двигателя потеряет половину своей скорости. Принять, что сила сопротивления движению катера изменяется пропорционально скорости (рис.3.5). двигателя и сила сопротивления
двигателя и сила сопротивления  , где k – коэффициент пропорциональности, зависящий от размеров, формы тела и свойств окружающей среды (рис.3.5а). Так как скорость постоянна, то эти силы по модулю равны. Таким образом, можно записать
, где k – коэффициент пропорциональности, зависящий от размеров, формы тела и свойств окружающей среды (рис.3.5а). Так как скорость постоянна, то эти силы по модулю равны. Таким образом, можно записать =
=  ,
, ,
, .
. .
. .
. .
. до
до  , а правую соответственно от нуля до t:
, а правую соответственно от нуля до t: ,
, .
. .
. , если сила сопротивления воздуха
, если сила сопротивления воздуха  , где α =56 кг/с.
, где α =56 кг/с. .
. , а
, а  ,
, или
или  .
. .
. и
и  =300 к горизонту. Найти скорость платформы, если снаряд застревает в песке (рис.3.6).
=300 к горизонту. Найти скорость платформы, если снаряд застревает в песке (рис.3.6). Представим на рисунке состояние платформы до и после попадания в нее снаряда. В данной ситуации система снаряд-платформа не является замкнутой. Как видно из рисунка импульс системы не сохраняется, по меньшей мере, он изменяет свое направление. Однако, считая, что в направлении оси OX не действует сила трения, можно воспользоваться законом сохранения импульса в проекции на данную ось
Представим на рисунке состояние платформы до и после попадания в нее снаряда. В данной ситуации система снаряд-платформа не является замкнутой. Как видно из рисунка импульс системы не сохраняется, по меньшей мере, он изменяет свое направление. Однако, считая, что в направлении оси OX не действует сила трения, можно воспользоваться законом сохранения импульса в проекции на данную ось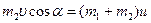 .
. .
. =0,4 кг/с, начальная масса ракеты m0 =1,2 кг. Какую скорость относительно Земли приобретет ракета через время t =1 с после начала движения?
=0,4 кг/с, начальная масса ракеты m0 =1,2 кг. Какую скорость относительно Земли приобретет ракета через время t =1 с после начала движения? .
. .
. .
.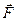 - сила – векторная величина, характеризующая действие одного тела на другое;
- сила – векторная величина, характеризующая действие одного тела на другое; - импульс силы – произведение вектора силы на время его действия.
- импульс силы – произведение вектора силы на время его действия. .
.


