
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия равновесия механической системыСодержание книги
Поиск на нашем сайте
По графику потенциальной кривой легко сделать ряд заключений о характере движения тела и условии его равновесия. Поясним это, используя зависимость
Данное условие выполняется при
При
функция Если полная энергия имеет значение Е, указанное на рис., то тело может совершать движение либо от x1 до x2, либо в пределах от x3 до бесконечности. В области x<x1 и x2<x<x3 тело проникнуть не может, так как потенциальная энергия не может стать больше полной энергии. Таким образом, область x2<x<x3 представляет собой потенциальный барьер, через который тело проникнуть не может, имея данный запас энергии. Область x1<x<x2 называется потенциальной ямой. В заключение отметим, что во многих разделах физики возникает необходимость в построении и анализе потенциальных кривых. Примеры решения задач
1. Сила, действующая на частицу, имеет вид Решение Элементарная работа согласно определению
Полную работу найдем путем интегрирования
Как следует из условия задачи, проекции силы на соответствующие координатные оси равны
С учетом этого, окончательно имеем
2. Тело массы m начинает двигаться под действием силы Решение По определению мгновенная мощность
Вектор скорости тела к моменту времени найдем путем интегрирования ускорения по времени
Вектор ускорения выразим из второго закона Ньютона
Подставляя найденное выражение в формулу для вектора скорости, имеем
С учетом полученного выражения мощность, развиваемая телом к моменту времени t равна
3. Потенциальная энергия частицы имеет вид Решение Вектор силы градиенту потенциальной энергии с обратным знаком
Учитывая, что
Тогда вектор силы действующей на частицу
где Работа, совершаемая над частицей при переходе ее из точки М(1,2,3) в точку N(2,3,4) равна убыли потенциальной энергии, т.е.
4. Какова минимальная работа, которую надо затратить, чтобы втащить волоком тело массы m на горку длины L и высоты H? Коэффициент трения равен Решение Чтобы втащить волоком тело массы m на горку длины L и высоты H, необходимо совершить работу против силы тяжести и силы трения. Следовательно
По определению эти работы соответственно равны
После подстановки, получим
где
5. Частица массы m1 испытывает упругое центральное столкновение с неподвижной частицей массы m2. Какую долю своей энергии
Решение Доля энергии, переданная первой частицей при столкновении со второй, выразится соотношением:
где При упругом столкновении выполняются законы механической энергии и сохранения импульса. Применяя эти законы, получим следующую систему
где Решая совместно уравнения, найдем
С учетом полученного выражения доля энергии, переданная первой частицей при столкновении со второй, будет равна
Основные положения 1. Элементарная работа – скалярное произведение вектора силы на вектор элементарного перемещения:
2. Работа переменной силы – определенный интеграл от функции
Единица работы – 1Дж=1Н.м. 3. Мощность – физическая величина, характеризующая скорость совершения работы:
Мгновенная мощность – скалярное произведение вектора силы на вектор скорости:
Единица мощности – 1Вт=1Дж/с. 4. Энергия – универсальная мера различных форм движения и взаимодействия, является функцией состояния системы. Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В классической механике механическая энергия системы равна сумме кинетической и потенциальной энергии:
5. Теорема о кинетической энергии – изменение кинетической энергии равно работе всех сил, действующих на тело:
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.86.132 (0.006 с.) |

 Потенциальной кривой называют график зависимости потенциальной энергии тела, находящегося в силовом поле, от координат. В некоторых простейших случаях, потенциальная энергия зависит только от одной координаты. Одним из таких примеров является тело, совершающее колебания в горизонтальной плоскости под действием упругих сил пружин. Другим примером может служить тело, находящееся в поле силы тяжести и скользящее без трения по изогнутой в вертикальной плоскости проволоке. Графики потенциальных кривых для данных случаев представлены на рис.4.9 и рис.4.10.
Потенциальной кривой называют график зависимости потенциальной энергии тела, находящегося в силовом поле, от координат. В некоторых простейших случаях, потенциальная энергия зависит только от одной координаты. Одним из таких примеров является тело, совершающее колебания в горизонтальной плоскости под действием упругих сил пружин. Другим примером может служить тело, находящееся в поле силы тяжести и скользящее без трения по изогнутой в вертикальной плоскости проволоке. Графики потенциальных кривых для данных случаев представлены на рис.4.9 и рис.4.10.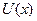 на рис.4.10.
на рис.4.10. Рассматриваемая система является замкнутой и консервативной, поэтому ее полная механическая энергия сохраняется, т.е.
Рассматриваемая система является замкнутой и консервативной, поэтому ее полная механическая энергия сохраняется, т.е.  . Из этого следует, что кинетическая энергия системы может возрастать только за счет уменьшения потенциальной энергии. В состоянии, когда
. Из этого следует, что кинетическая энергия системы может возрастать только за счет уменьшения потенциальной энергии. В состоянии, когда  , а
, а 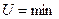 , система не может прийти в движение без воздействия извне, т.е. будет находиться в равновесии. Условие минимума потенциальной энергии имеет вид
, система не может прийти в движение без воздействия извне, т.е. будет находиться в равновесии. Условие минимума потенциальной энергии имеет вид
 . (4.36)
. (4.36) и соответствует состоянию устойчивого равновесия.
и соответствует состоянию устойчивого равновесия. (4.37)
(4.37)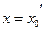 максимум, что соответствует состоянию неустойчивого равновесия.
максимум, что соответствует состоянию неустойчивого равновесия.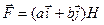 , где
, где  и b – константы. Вычислить работу, совершаемую над частицей этой силой на пути от точки с координатами (1,2,3) м до точки с координатами (3,4,5) м.
и b – константы. Вычислить работу, совершаемую над частицей этой силой на пути от точки с координатами (1,2,3) м до точки с координатами (3,4,5) м. .
. .
. ,
,  , а
, а  ,
,  .
. .
. . Найти мощность
. Найти мощность  , развиваемую силой в момент времени t.
, развиваемую силой в момент времени t. .
. .
. .
. .
. .
. , где r – модуль радиус-вектора частицы,
, где r – модуль радиус-вектора частицы, 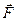 , действующую на частицу, и работу, совершаемую над частицей при переходе ее из точки М(1,2,3) в точку N(2,3,4).
, действующую на частицу, и работу, совершаемую над частицей при переходе ее из точки М(1,2,3) в точку N(2,3,4). ,
, 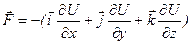 .
. , частные производные потенциальной энергии по координатам будут равны
, частные производные потенциальной энергии по координатам будут равны ,
, 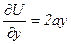 ,
, 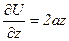 .
.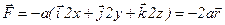 ,
, .
. =
= .
. .
. .
.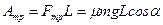 ,
,  .
.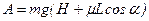 ,
, .
. первая частица передала второй?
первая частица передала второй? ,
, - кинетическая энергия первой частицы до столкновения,
- кинетическая энергия первой частицы до столкновения,  - приобретенная кинетическая энергия второй частицы.
- приобретенная кинетическая энергия второй частицы.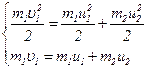 ,
, и
и 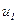 - скорости первой частицы до и после столкновения соответственно,
- скорости первой частицы до и после столкновения соответственно,  - скорость второй частицы после столкновения.
- скорость второй частицы после столкновения. .
. .
.
 в пределах от
в пределах от 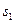 до
до 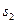 :
: .
. .
. .
.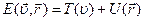
 .
.


