
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные случаи кинематики материальной точки
а) Равномерное прямолинейное движение В случае движения точки вдоль положительного направления оси ОX
Зависимость координаты x точки от времени найдем интегрированием
Путь при равномерном прямолинейном движении
Графики пути и скорости равномерного прямолинейного движения представлены на рис. 1.7. б) Равнопеременное прямолинейное движение В этом случае Зависимость величины скорости от времени имеет вид
где При движении вдоль положительного направления оси ОX координата изменяется по закону
Графики пути и скорости равнопеременного прямолинейного движения представлены на рис. 1.8.
в) Равномерное движение по окружности
Поместим начало системы координат в центр окружности, по которой движется точка, и пусть в начальный момент времени она находилась в наивысшей точке А (рис.1.9). Обозначим меняющийся со временем угол между
а уравнение траектории г) Движение тела, брошенного под углом к горизонту Пусть тело брошено под углом α к горизонту со скоростью В выбранной декартовой системе координат вектор скорости и радиус-вектор меняются по закону
В соответствии с принципом независимости движений это движение можно разложить вдоль координатных осей на два прямолинейных. Движение тела вдоль оси OX будет равномерным (gx=0), а вдоль оси OY равнопеременным (gy=-g), при этом проекции начальной скорости равны
Проектируя уравнения (1.34) и (1.35) на оси координат, получим следующую систему уравнений
Решение данной системы уравнений позволяет определить время полета, максимальную высоту подъема и дальность полета. В наивысшей точке подъема вертикальная составляющая скорости
В момент времени Решая систему кинематических уравнений, получим уравнение траектории движения тела
Нетрудно видеть, что данное уравнение представляет собой параболу (см. рис.1.10). Радиус кривизны данной траектории в любой ее точке можно определить, используя формулу нормального ускорения (1.21). Так, в наивысшей точке траектории
Примеры решения задач
На основе известных кинематических уравнений, выражающих зависимость радиус-вектора или координат движущейся точки от времени, путем дифференцирования можно найти вектор скорости и его компоненты, а также и величину скорости. Двукратным дифференцированием кинематических уравнений мы получим зависимость от времени компонент ускорения. Данные задачи называются прямыми задачами кинематики. Возможны также обратные задачи: по функциям, выражающим зависимость компонент ускорения, можно найти координаты точки в заданный момент времени. Эти задачи решаются интегрированием: однократное интегрирование дает зависимость от времени компонент скорости, двукратное – зависимость от времени координат. При этом в формулах появляются постоянные интегрирования, которые могут быть определены из так называемых начальных условий. Начальные условия – это параметры движения в некоторый определенный момент времени, например, начальный. Начальные условия должны быть заданы дополнительно, поскольку в противном случае задача становится неопределенной. Приведем примеры решения прямых и обратных задач кинематики. 1. Радиус-вектор материальной точки изменяется со временем по закону Решение Из представленного уравнения
Исключив из полученной системы уравнений время, найдем уравнение траектории материальной точки
Полученное уравнение представляет собой уравнение параболы. Вектор скорости точки найдем, взяв производную от радиус-вектора по времени
Модуль скорости определим через его проекции на координатные оси
В момент времени Вектор ускорения получим, дифференцируя скорость по времени
Данный вектор направлен вдоль оси OY, а его величина не зависит от времени и равна 16 м/с2. 2. Две материальные точки движутся по одной прямой, совпадающей осью OX. В начальный момент времени первая точка имела координату
где Решение Условием встречи является равенство координат точек. Поэтому определим интегрированием кинематические уравнения их движения
Константы С1 и С2 определим из начальных условий:
Приравняем эти выражения в момент встречи
Выполнив преобразования, находим
Выбирая положительное значение корня, получим Ускорения первой и второй точек находим, взяв производные от скорости по времени
Подставляя в эти уравнения значение времени встречи, получим ответ
3. Тело брошено горизонтально со скоростью Решение Выберем систему координат и покажем траекторию движения тела, его скорость, ускорение и их составляющие в некоторый момент времени t (рис.1.11).
Полное ускорение тела и его нормальная составляющая
где Произведя подстановку, получим окончательно
4. Ускорение парашютиста в затяжном прыжке из неподвижного вертолета изменяется по закону
где
Зависимость скорости от времени парашютиста найдем путем интегрирования
Максимальное значение скорости определится из условия
Искомое время найдем из решения уравнения
После преобразования, получим
График зависимости скорости от времени представлен на рис.1.12.
5. Скорость самолета при разгоне на взлетной полосе изменяется по закону
где Решение Длину пути при разгоне самолета определим интегрированием скорости в пределах от нуля до
Произведя вычисления, получим S=1260 м. Основные положения 1. Радиус-вектор – вектор, соединяющий начало координат с положением материальной точки в произвольный момент времени:
2. Скорость – векторная физическая величина, равная производной радиус-вектора по времени:
Проекции скорости на координатные оси равны первым производным по времени от соответствующих координат:
Вектор скорости направлен по касательной к траектории в сторону движения тела. Величина скорости – скалярная величина, равная производной пути по времени:
3. Ускорение – векторная физическая величина, равная первой производной от вектора скорости по времени или второй производной радиус-вектора по времени:
Проекции ускорения на координатные оси равны вторым производным по времени от соответствующих координат:
|
|||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.255.162 (0.05 с.) |
 и
и  .
. ,
,  ,
,  , (1.30)
, (1.30) где
где  - координата точки в начальный момент времени.
- координата точки в начальный момент времени.
 . Если
. Если  , то движение называют равноускоренным, а если
, то движение называют равноускоренным, а если 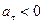 - равнозамедленным. Ради простоты вместо
- равнозамедленным. Ради простоты вместо  пишут просто
пишут просто  .
. ,
,  , (1.31)
, (1.31) - скорость в начальный момент времени.
- скорость в начальный момент времени. ,
,  , (1.32)
, (1.32) а уравнение пути
а уравнение пути . (1.33)
. (1.33)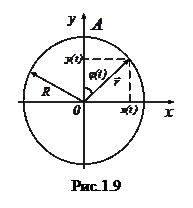 Величина скорости остается неизменной (
Величина скорости остается неизменной ( ), но ее направление постоянно изменяется (
), но ее направление постоянно изменяется ( ), причем
), причем .
. и OY через
и OY через  . Тогда кинематические уравнения движения будут иметь вид
. Тогда кинематические уравнения движения будут иметь вид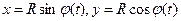 ,
, .
.
 , (1.34)
, (1.34) . (1.35)
. (1.35) (1.36)
(1.36)

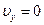 , следовательно, время подъема
, следовательно, время подъема  , а высота подъема над горизонтом в этот момент
, а высота подъема над горизонтом в этот момент  .
. тело упадет на землю, пройдя вдоль оси Oх расстояние
тело упадет на землю, пройдя вдоль оси Oх расстояние  При заданной начальной скорости максимальная дальность полета достигается при
При заданной начальной скорости максимальная дальность полета достигается при  , то есть при
, то есть при  .
.
 . (1.37)
. (1.37) , а
, а  , отсюда
, отсюда . (1.38)
. (1.38) . Определите:1) уравнение траектории материальной точки; 2) вектор скорости точки в зависимости от времени; 3) вектор ускорения точки в зависимости от времени; 4) модули скорости и ускорения точки в момент времени
. Определите:1) уравнение траектории материальной точки; 2) вектор скорости точки в зависимости от времени; 3) вектор ускорения точки в зависимости от времени; 4) модули скорости и ускорения точки в момент времени 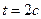 .
.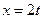 и
и 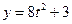 .
. .
. .
. .
. 32,06 м/с.
32,06 м/с.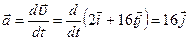 .
. м, а вторая
м, а вторая  м. Скорости точек изменяются по законам
м. Скорости точек изменяются по законам и
и  ,
, ,
,  . Определить ускорения точек в момент их встречи.
. Определить ускорения точек в момент их встречи. ,
, .
. и С1=0;
и С1=0;  и С2=0. Тогда кинематические уравнения примут вид
и С2=0. Тогда кинематические уравнения примут вид ,
, .
.
 .
. .
. .
. и
и  .
. ,
, 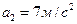 .
. м/с. Пренебрегая сопротивлением воздуха, определите радиус кривизны траектории тела через
м/с. Пренебрегая сопротивлением воздуха, определите радиус кривизны траектории тела через  с после начала движения.
с после начала движения. Проекции скорости на координатные оси и ее величина в данный момент времени будут равны
Проекции скорости на координатные оси и ее величина в данный момент времени будут равны ,
,  ,
, .
. ,
,  ,
, .
. , R =140 м.
, R =140 м. ,
, ,
,  . Через какое время после начала прыжка скорость парашютиста станет равной половине максимального значения? Постройте график зависимости скорости от времени
. Через какое время после начала прыжка скорость парашютиста станет равной половине максимального значения? Постройте график зависимости скорости от времени Решение
Решение
 при
при  , следовательно
, следовательно  .
. .
. с.
с. ,
, ,
, 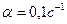 ,
,  - время от начала движения. Определите длину пути при разгоне, если он длился 10 с.
- время от начала движения. Определите длину пути при разгоне, если он длился 10 с.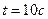
 .
. ,
,  .
. ,
, 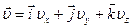 .
. .
. ,
, 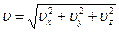 .
. ,
,  .
. .
.


