
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные элементарных функций
Элементы интегрального исчисления Понятие об интеграле. Пусть задана функция
Таким образом геометрический смысл определенного интеграла – площадь фигуры ограниченной ординатами графика Функция
Вычисление интеграла сводится к нахождению функции по данному выражению ее дифференциала. Неопределенным интегралом данной функции
где С – постоянная интегрирования, определяемая из начальных условий. Если известно, что при данном значении аргумента
Свойства неопределенного интеграла: · знак дифференциала перед знаком интеграла уничтожает последний:
· постоянный множитель можно выносить за знак интеграла:
· интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов:
Таблица П1.2 Первообразные элементарных функций
Используя свойства неопределенного интеграла, можно в ряде случаев свести интегрирование к табличным формулам. При интегрировании способом подстановки вместо переменной x вводят вспомогательную переменную z=z(x). Тогда подынтегральное выражение преобразуется в более простой вид, что облегчает интегрирование
Пример: Введемпеременную z = 2x - 1, дифференцируя, получаем dz=2dx, откуда dx=dz/2. Тогда подынтегральное выражение примет вид
Возвращаясь к переменной x, находим:
Интегрированием по частям называется сведение данного интеграла
Примеры: 1) Представляем подынтегральное выражение в виде
2) Подынтегральную функцию представим в виде
Для вычисления интегралов вида
удобно пользоваться формулами
Пример:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.22.135 (0.009 с.) |












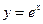









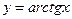

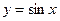



 и надо найти площадь «криволинейной трапеции» аАBb. Разобьем площадь под кривой на n частей и построим ступенчатую фигуру, показанную штриховкой на рис.П1.10. Предел суммы площадей «прямоугольных ступенек» при
и надо найти площадь «криволинейной трапеции» аАBb. Разобьем площадь под кривой на n частей и построим ступенчатую фигуру, показанную штриховкой на рис.П1.10. Предел суммы площадей «прямоугольных ступенек» при  и есть интеграл. Обозначение
и есть интеграл. Обозначение

 ; работа силы:
; работа силы:  . Кроме того с помощью определенного интеграла можно вычислить массу, момент инерции и т.п.
. Кроме того с помощью определенного интеграла можно вычислить массу, момент инерции и т.п. называется первообразной от функции
называется первообразной от функции  , если выполняется равенство
, если выполняется равенство .
.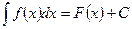 ,
, функция принимает значение
функция принимает значение  , то С находится из соотношения
, то С находится из соотношения .
.


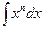
 ,
, 






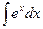















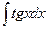











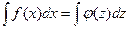 .
. .
. .
.
 к интегралу
к интегралу  с помощью формулы
с помощью формулы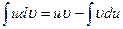 .
. .
. . Здесь роль
. Здесь роль  играет
играет  , роль
, роль  - функция
- функция  . Тогда
. Тогда

 (здесь
(здесь  ,
,  ), это дает
), это дает =
=
 ,
, 
 ,
,  .
. =
= 



