
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение динамики для твердого тела, вращающегося вокруг неподвижной оси
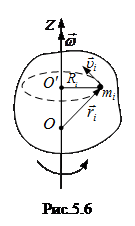
Применим уравнение моментов относительно оси к рассмотрению вращательного движения твердого тела. Рассмотрим твердое тело произвольной формы, вращающееся относительно неподвижной оси (рис.5.6). За ось моментов OZ удобно выбрать ось вращения, направив ее по угловой скорости Уравнение моментов в этом случае имеет вид
где Найдем связь между моментом импульса тела Момент импульса материальной точки
где Учитывая, что
Момент импульса относительно данной оси всего тела определится суммированием по всем элементарным точкам
Величина
Используя (5.18), получим искомую связь между
Таким образом, момент импульса тела относительно оси равен произведению момента инерции тела на его угловую скорость относительно данной оси. С учетом полученного соотношения (5.19) уравнение моментов принимает вид
т.е. произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси. Полученное уравнение представляет собой основное уравнение динамики вращательного движения тела вокруг неподвижной оси. Оно аналогично уравнению второго закона Ньютона (основного уравнения динамики поступательного движения). Роль массы выполняет момент инерции тела, роль силы – момент силы, роль линейного ускорения – угловое ускорение. Момент инерции тела относительно оси является мерой инертности тела к изменению его угловой скорости. Чем больше момент инерции тела, тем труднее изменить ее скорость. При одном и том же значении момента силы тело с большим значением момента инерции приобретает меньшее угловое ускорение.
Вычисление моментов инерции. Теорема Штейнера
Момент инерции твердого тела зависит от массы и ее распределения относительно оси вращения. Вычисление момента инерции сводится к суммированию в случае дискретного распределения массы:
где При непрерывном распределении массы в объеме V суммирование должно быть заменено интегрированием по формулам:
где Рассмотрим несколько примеров расчета момента инерции для тел простейшей формы относительно оси, проходящей через центр масс. 1) Момент инерции кольца, обруча или тонкостенного цилиндра массы m и радиуса R.
2) Момент инерции диска или сплошного однородного цилиндра массы m и радиуса R относительно его оси.
где ρ – плотность диска. Момент инерции рассматриваемого элемента равен
а всего диска
Ввиду однородности диска его масса равна
С учетом этого окончательно, получим
С учетом того, что масса полого цилиндра равна
имеем
3) Момент инерции однородного тонкого стержня массы m и длины l относительно оси, проходящей перпендикулярно стержню через его середину.
где ρ – плотность стержня, приходящаяся на единицу его длины. Момент инерции всего стержня находим, интегрируя данное выражение в пределах от 0 до
Так как
Выделим тонкий диск радиуса r и толщиной dz, удаленный от центра шара на расстояние z (рис.5.11). Масса этого диска равна
где Момент инерции данного диска определяется формулой
Момент инерции шара найдем интегрированием по z в пределах от 0 до R, с последующим удвоением результата, в силу симметрии задачи
Вводя в данную формулу массу шара, равную
получим окончательно
В качестве примера, рассчитаем момент инерции стержня относительно оси перпендикулярной стержню и проходящей через его конец (рис.7.12). По теореме Штейнера будем иметь
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.127 (0.009 с.) |
 (
( ).
).
 ,
, - результирующий момент внешних сил, вызывающий вращение тела, относительно оси OZ.
- результирующий момент внешних сил, вызывающий вращение тела, относительно оси OZ.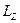 и угловой скоростью ω. С этой целью мысленно разобьем тело на элементарные массы
и угловой скоростью ω. С этой целью мысленно разобьем тело на элементарные массы  , которые можно рассматривать как материальные точки.
, которые можно рассматривать как материальные точки. ,
,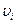 и
и  - скорость i- той материальной точки и радиус окружности, которую она описывает при вращении тела.
- скорость i- той материальной точки и радиус окружности, которую она описывает при вращении тела. , где ω – угловая скорость вращения, одинаковая для всех точек тела, получим
, где ω – угловая скорость вращения, одинаковая для всех точек тела, получим . (5.16)
. (5.16) . (5.17)
. (5.17) , равная сумме произведений элементарных масс на квадрат их расстояний от некоторой оси, называется моментом инерции тела относительно данной оси:
, равная сумме произведений элементарных масс на квадрат их расстояний от некоторой оси, называется моментом инерции тела относительно данной оси: . (5.18)
. (5.18)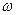 :
: . (5.19)
. (5.19) или
или  , (5.20)
, (5.20) ,
, - радиус вращения массы
- радиус вращения массы  , (5.21)
, (5.21) - плотность материала,
- плотность материала,  - радиус вращения элемента объема
- радиус вращения элемента объема  , имеющего массу
, имеющего массу  .
. Все малые элементы тела находятся на одном и том же расстоянии от его оси, проходящей через центр масс (рис.5.7). Поэтому
Все малые элементы тела находятся на одном и том же расстоянии от его оси, проходящей через центр масс (рис.5.7). Поэтому . (5.22)
. (5.22) Внутри диска выделим тонкое кольцо радиуса r толщиной dr и шириной, равной ширине диска h (рис.5.8). Объем и масса такого кольца равны:
Внутри диска выделим тонкое кольцо радиуса r толщиной dr и шириной, равной ширине диска h (рис.5.8). Объем и масса такого кольца равны: и
и  ,
, ,
, . (5.23)
. (5.23) .
. . (5.24)
. (5.24) Аналогично, момент инерции полого толстостенного цилиндра (рис.5.9) с внешним радиусом R2 и внутренним R1 можно представить в виде интеграла (5.23), но пределы интегрирования считать равными R1 и R2:
Аналогично, момент инерции полого толстостенного цилиндра (рис.5.9) с внешним радиусом R2 и внутренним R1 можно представить в виде интеграла (5.23), но пределы интегрирования считать равными R1 и R2: . (5.25)
. (5.25) ,
, . (5.25)
. (5.25) Разобьем стержень на элементарные отрезки dx (рис.5.10). Тогда
Разобьем стержень на элементарные отрезки dx (рис.5.10). Тогда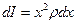 ,
, , с последующим его удвоением
, с последующим его удвоением .
. , то
, то . (5.26)
. (5.26) 4). Момент инерции шара массы m и радиуса R относительно оси OZ.
4). Момент инерции шара массы m и радиуса R относительно оси OZ. ,
, .
. .
. .
. ,
, . (5.27)
. (5.27) Расчет момента инерции тела относительно произвольной оси облегчается, если использовать теорему Штейнера. В соответствии с этой теоремой, момент инерции относительно произвольной оси
Расчет момента инерции тела относительно произвольной оси облегчается, если использовать теорему Штейнера. В соответствии с этой теоремой, момент инерции относительно произвольной оси  равен сумме моментов инерции тела
равен сумме моментов инерции тела 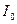 относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между этими осями
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между этими осями . (5.28)
. (5.28) . (5.29)
. (5.29)


