Теоретичні відомості про циліндр, конус та їх поверхню. Методичні вказівки до виконання роботи.

Прямим круговим циліндром називається тіло, утворене обертанням прямокутника навколо його сторони

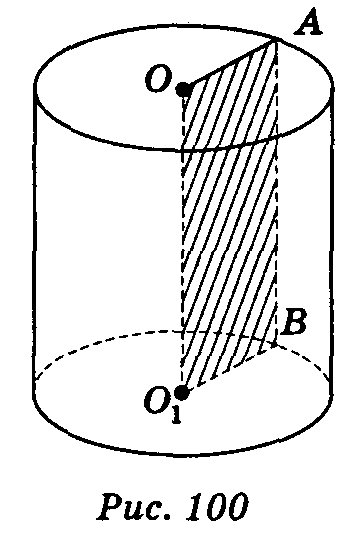
Сторони ОА і 0₁В описують рівні круги, які лежать у паралель­них площинах і називаються основами циліндра

Радіуси кругів на­зиваються радіусами циліндра. Сторона АВ описує поверхню, яка називається бічною поверхнею циліндра. Відрізки бічної поверхні, які паралельні і дорівнюють АВ, називаються твірними циліндра

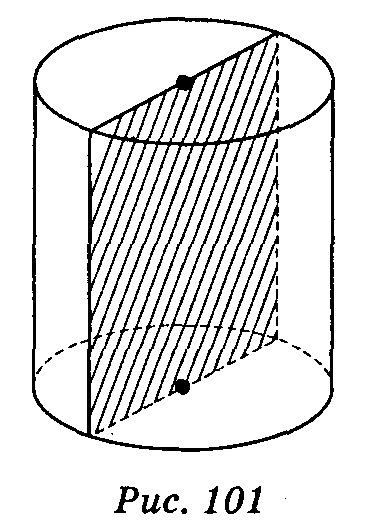Висотою циліндра називається відрізок, перпендикулярний до основ циліндра, кінці якого належать основам. Висота циліндра до­рівнює його твірній.

Осьовий переріз циліндра — прямокутник зі сторонами, що до­рівнюють висоті циліндра і діаметру його основи.

Площею бічної і повної поверхні циліндра називають площу розгортки бічної і повної поверхні. Тоді площа бічної поверхні S_біч і пло­ща повної поверхні S_цил визначаються формулами:

S_біч = 2πRH, S_цил = 2πRH + 2πR ² = 2πR(H + R), де R, Н — радіус і висота циліндра відповідно

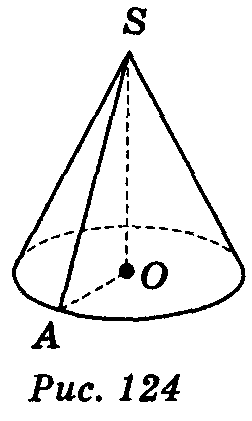
Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів

Якщо прямокутний трикутник SАО обертається навколо катета SO, то його гіпотенуза описує бічну поверхню, а катет ОА — круг — основу конуса. Радіус цього круга називається радіусом конуса; то­чка S, відрізок SА, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.

Осьовий переріз конуса — переріз конуса площиною, яка проходить через його вісь.

Таким чином, площа бічної поверхні конуса дорівнює добутку поло­вини довжини кола основи та твірну: S_біч = πR l.

Площею повної поверхні конуса називається сума площ бічної пове­рхні та основи. Для обчислення площі повної поверхні конуса S_к одер­жуємо формулу

S_к = πR (l + R).

Задача №1. Хорда довжиною а стягує в основі циліндра дугу φ. Висота цилінд­ра дорівнює Н. Знайдіть площу повної поверхні циліндра.

Теоретичні відомості про об’єм циліндра

Об’єм циліндра обчислюється за допомогою формули:

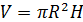, де R радіус циліндра, H – його висота.

Задача №2. У циліндрі, паралельно його осі, проведено площину. Вона перети­нає основу по хорді, яку видно із центра цієї основи під кутом α. Діагональ утвореного перерізу дорівнює d і нахилена до основи під кутом β. Знайдіть об'єм циліндра.