
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості про комбінації. Методичні вказівки до виконання роботи.Содержание книги
Поиск на нашем сайте
Нехай дано множину {а, b, с}. З елементів цієї множини можна утворити 6 двохелементних розміщень. ab, ас, bс, bа, са, сb. Це впорядковані підмножини даної множини. А скільки не-впорядкованих двохелементних підмножин можна скласти з тих самих елементів? Тільки три: {ab}, {ас}, {be}. Будь-яка підмножина з т елементів даної множини, яка містить n елементів, називається комбінацією з n елементів по т елементів. Число комбінацій з n елементів по т позначають символом З чотирьох елементів множини {a, b, c, d} можна утворити 6 комбінацій по 2 елементи: {а, b }, { а, с }, { а, d }, {b, с }, { с, а }, { b. d }; 3 комбінації по 3 елементи: { а, b, с }, { а, b, d }, { b, с, d }. Таким чином, Домовилися вважати, що
Виведемо формулу для знаходження значень Кожну m -елементну комбінацію можна впорядкувати Р m способами. У результаті з однієї комбінації утворюється
Число комбінацій з n елементів по т дорівнює дробу, чисельник якого е добуток т послідовних натуральних чисел, найбільше з яких n, а знаменник дробу — добуток т послідовних натуральних чисел. Враховуючи, що Задача №5. Скількома способами можна закреслити 6 номерів із 49 в картці «Спортлото».
Задача №6. Обчисліть:
1) Що таке невпорядкована множина? 2) Що таке перестановка? 3) Яка множина називається впорядкованою? 4) Що таке розміщення? 5) Що таке комбінація? 6) Що таке трикутник Паскаля? 7) Скільки різних чотирицифрових чисел можна утворити з цифр 0, 1, 2, 3, не повторюючи цифри у запису числа? 8) В одинадцятому класі 30 учнів. Вони обмінялись один із одним фотокартками. Скільки фотокарток було роздано? Висновок.______________________________________________________________________________________________________________________________________________________________________________________________ Перевірив викладач_____________Оцінка _________ Дата______ ПРАКТИЧНА РОБОТА №25 Тема Обчислення ймовірності за допомогою комбінаторики, ймовірності суми та добутку подій Мета роботи: навчитись розв’язувати задачі на застосування основних формул комбінаторики Наочне забезпечення та обладнання: 1. Інструкційні картки; 2. Приклади задач; 3. Роздаткові матеріали: опорні конспекти “Основні формули комбінаторики” 4. Обчислювальні засоби: калькулятор.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.239.157 (0.008 с.) |

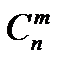 . Наприклад:
. Наприклад: 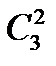 = 3.
= 3.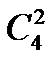 = 6,
= 6, 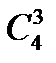 = 3.
= 3.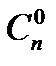 = 1,
= 1, 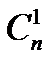 =n,
=n, 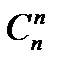 = 1.
= 1.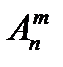 при одних і тих же значеннях т і п.
при одних і тих же значеннях т і п.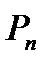 •
• 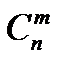 , звідси
, звідси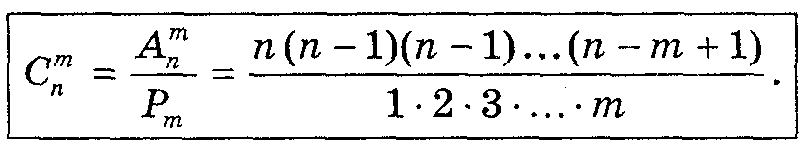
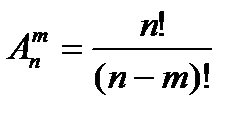 можна одержати
можна одержати 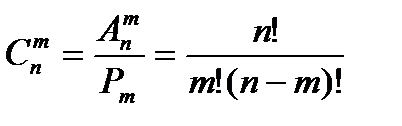 . Отже,
. Отже, 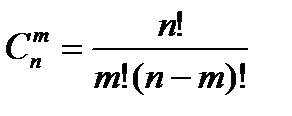
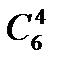 +
+ 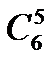 +
+ 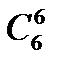 .
. Питання для самоконтролю знань і вмінь
Питання для самоконтролю знань і вмінь


