Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості про застосування похідної.Содержание книги
Поиск на нашем сайте
Фізичний зміст похідної. При прямолінійному русі точки швидкість в даний момент Прискорення
Задача №3. Знайти швидкість і прискорення точки, що рухається за законом Геометричний зміст похідної. Похідна Задача №4. а)Скласти рівняння дотичної до графіка функції б) В яких точках дотична до графіка функції
1. Похідна суми, добутку, частки двох функцій. 2. Похідна складеної функції. 3. Похідна степеневої функції. 4. Похідні логарифмічної, показникової та тригонометричних функцій. 5. Фізичний зміст похідної. 6. Геометричний зміст похідної. Рівняння дотичної до графіка функції.
Висновок.______________________________________________________________________________________________________________________________________________________________________________________________ Перевірив викладач___________Оцінка _________ Дата_______
ПРАКТИЧНА РОБОТА №17 Тема. Дослідження функцій та побудова графіків функцій за допомогою похідної
Мета роботи: навчитись досліджувати функції та будувати їх графіки за допомогою похідної Наочне забезпечення та обладнання: 1. Інструкційні картки; 2. Приклади задач; 3. Роздаткові матеріали: опорні конспекти «схема дослідження функції за допомогою похідної» 4. Обчислювальні засоби: калькулятор.
Теоретичні відомості про схему дослідження функції за допомогою похідної. Методичні вказівки до виконання роботи.
Схема дослідження функцій і побудови графіків за допомогою похідної 1. Знайти область визначення функції. 2. Встановити парність (непарність) і періодичність функції. 3. Визначити точки перетину графіка функції з осями координат. 4. Визначити інтервали зростання й спадання функції. 5.Знайти точки екстремуму та обчислити значення функції у цих точках. 6.Дослідити поведінку функції на кінцях проміжків області визначення 7.Якщо необхідно, знайти координати додаткових точок, щоб уточнити поведінку графіка функції. 8.Виконати побудову графіка функції. Відзначимо, що ця схема є орієнтовною і не завжди потрібно виконувати її повністю. Наприклад, далеко не завжди можна точно знайти точки перетину графіка з віссю Оx, навіть якщо ми знаємо, що такі точки існують. Також часто достатньо складно дослідити поведінку функції на кінцях проміжків області визначення. У такому випадку уточнити поведінку графіка функції можна за рахунок знаходження координат точок графіка
функції, абсциси яких вибирають так, щоб вони наближалися до кінців проміжків області визначення. Задача № 1. Дослідити функцію та побудувати її графік
Задача №2. Дослідити функцію та побудувати її графік
|

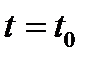 дорівнює похідній
дорівнює похідній 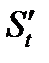 від шляху
від шляху 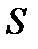 по часу
по часу 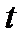 , обчисленій при
, обчисленій при 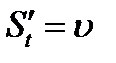 .
.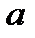 в даний момент
в даний момент 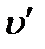 від швидкості
від швидкості 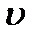 по часу
по часу 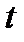 , обчисленій при
, обчисленій при 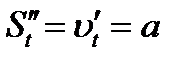 .
.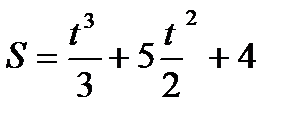 в момент часу
в момент часу 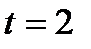 .
.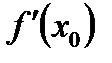 дорівнює кутовому коефіцієнту
дорівнює кутовому коефіцієнту 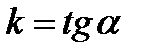 дотичної до кривої, проведеної у точці
дотичної до кривої, проведеної у точці 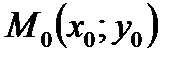 . Рівняння дотичної до графіка функції
. Рівняння дотичної до графіка функції 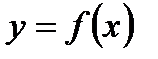 в точці з абсцисою
в точці з абсцисою 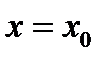 має вигляд:
має вигляд: 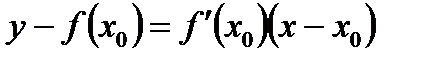 .
.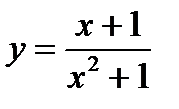 в точці з абсцисою
в точці з абсцисою 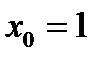 .
.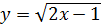 утворює з віссю абсцис кут 450?
утворює з віссю абсцис кут 450? Питання для самоконтролю знань і вмінь
Питання для самоконтролю знань і вмінь