
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формирования портфеля проектовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как отмечалось выше, специфика управления портфелями проектов заключается, в том числе, в том, что целесообразность реализации отдельных проектов оценивается с точки зрения стратегии организации в целом, то есть в общем случае - по нескольким критериям, однозначная оценка проекта по которым не всегда возможна. Кроме того, проекты требуют затрат ресурсов, как минимум, нескольких видов (в отличие от инвестиционных портфелей или портфелей ценных бумаг, описываемых лишь финансовыми показателями). Поэтому обобщим "задачу о ранце" на случай, во-первых, многокритериальных нечетких оценок проектов, и, во-вторых, на случай использования при реализации проектов ресурсов нескольких видов. Рассмотрим следующую модель. Пусть имеется m видов ресурсов и известно, что каждый проект i ∈N требует ресурсы cij, j ∈M= {1, 2, …,m } - множеству ресурсов. Будем считать, что каждый проект i ∈ N оценивается по k критериям, оценки ац по которым принимают значения из множеств Al, l ∈ K = {1, 2, …,k } - множеству критериев. Введем предположение об аддитивности оценок и ресурсов по проектам: оценка портфеля по каждому критерию получается суммированием оценок по данному критерию по всем проектам, входящим в портфель; ресурсы каждого вида, требуемые для реализации портфеля проектов, определяются суммированием количеств ресурса данного вида по всем проектам, входящим в портфель. Отметим, что, если отказаться от этого предположения, то в общем случае для решения задачи формирования портфеля необходимо сравнивать все (!) возможные портфели. Портфель Q ⊆N характеризуется векторной оценкой aQ = (aQ1, aQ2, …, aQk), где aql = ∑a il, l ∈ K, и вектором требуемых ресурсов «eg cQ = (cQ1, cQ2, …, cQm), гдеcQj= Yscij J M Под ресурсным ограничением будем понимать следующее. Пусть известны имеющиеся в организации ресурсы каждого вида, которые могут быть использованы для реализации проектов: R = (R1, R2,…, Rm). Портфель Q будем считать удовлетворяющим ресурсным ограничениям, если выполнено: Задача формирования портфеля может формулироваться следующим образом: либо найти все допустимые (удовлетворяющие ресурсному ограничению (1)) оптимальные по Парето портфели1 и предоставить лицу, принимающему решения, возможность выбора из этого множества; либо (если задана функция агрегирования оценок F(aq), отображающая множество ∏Al в любое упорядо- ык ченное множество) найти оптимальный (допустимый и наилучший с точки зрения значения функции агрегирования) портфель2. Для решения этой задачи может быть использован следующий алгоритм. Построим на плоскости следующую сеть: из начальной точки (0; 0) отложим две дуги, соответствующие включению или невключению первого проекта в портфель. Горизонтальная дуга (невключение проекта в портфель) не требует ресурсов и не дает никакого эффекта. Наклонной дуге (включение проекта в портфель) поставим в соответствие два вектора - вектор ресурсов c1 = (c11, c12,…, c1m) и вектор эффекта a1 = (a11, a12, …,a 1k). Далее, продолжая аналогично (суммируя покомпонентно соответствующие ресурсы и эффекты по всем проектам, включенным в тот или иной портфель, описываемый путем из начальной точки) для второго, третьего и т.д. проектов (до n-го включительно), получим в общем случае 2n вариантов.
2 Отметим, что, если функция F(-) — непрерывная и монотонно возрастающая, то оптимальный портфель будет эффективен по Парето. Если в некоторой точке "пересекаются" два пути, то есть два набора проектов характеризуются одинаковыми затратами ресурсов (что, как правило, делает метод динамического программирования более эффективным, чем простой полный перебор), то, если один набор Парето-доминирует другой по критериальным оценкам, то следует оставить доминирующие оценки, если же доминирования нет, то следует в дальнейшем (добавляя новые проекты) рассматривать обе комбинации оценок. Для каждого из окончательных вариантов рассчитываем вектор затрат ресурсов и вектор эффектов. Достоинством описанного метода является то, что при добавлении новых проектов - претендентов на включение в портфель, или исключении части имеющихся, нет необходимости пересчитывать заново все варианты. Это возможно в силу введенного выше предположения об аддитивности оценок и аддитивности ресурсов. В результате получаем в общем случае 2 n портфелей, каждый из которых описывается двумя векторами - затрат и эффектов (всего - т-к числами). Затем исключаем портфели, нарушающие ресурсное ограничение (1) (если оно фиксировано, то проверять его можно и в процессе построения сети, сразу оставляя только допустимые портфели), и портфели, доминируемые по Парето с точки зрения затрат и эффектов (такую проверку также можно осуществлять в процессе построения сети, сразу оставляя только недоминируемые портфели). В результате получаем множество допустимых и эффективных по Парето портфелей проектов. Завершив описание алгоритма, отметим, что далее возникает задача многокритериальной оптимизации (принятия решений при многих критериях), для решения которой существует множество детально проработанных методов [129]. Число вариантов (возможных портфелей) быстро растет с ростом числа проектов-претендентов1. Понятно, что даже при не очень большом числе претендентов содержательный анализ всех вариантов затруднителен, особенно в случае многих критериев, поэтому необходима разработка процедур сокращения числа (предварительного отбора) анализируемых вариантов. Одной из таких процедур является используемая в приведенном выше алгоритме процедура отсева неэффективных вариантов в процессе построения сети, соответствующей методу динамического программирования. Сократив число вариантов, можно применять те или иные процедуры выбора окончательного множества проектов, включаемых в портфель. Для этого в случае одного вида ресурса и двух критериев оценки проектов (k = 2) удобно использовать следующий прием: нанесем на плоскости точки, соответствующие отобранным портфелям и проставим около каждой точки соответствующие затраты. Примерами использования такого подхода являются: так называемые РЭСТ-диаграммы (в случае, когда критериями являются эффект и риск) [28] и модели отбора предприятий на получение налоговых льгот [32]. Полученная диаграмма, во-первых, может служить основой для обсуждения и согласования окончательных вариантов портфеля проектов, и, во-вторых, позволяет ставить и решать ряд практически важных задач: определения "минимальных" затрат, обеспечивающих достижение заданного вектора оценок, принятия решений о целесообразности взятия кредита для финансирования части проектов и т.д. Отметим, что рассмотренная в настоящем разделе модель в случае скалярных оценок и одного вида ресурса переходит в описанный в [33, 32,41] метод "затраты-эффект". Нечеткая модель. Выше рассмотрена многокритериальная модель формирования портфеля проектов, в которой требуемые для
реализации проектов количества ресурсов и оценки эффекта были четкими. Если для получения информации о затратах ресурсов можно использовать нормативы или ретроспективные данные, то эффект от реализации проекта, особенно с точки зрения стратегических целей организации, не всегда можно оценить однозначно. Поэтому целесообразным представляется использование нечетких оценок эффекта от реализации проектов. Данные оценки могут быть получены, в том числе, экспертным путем. Рассмотрим многокритериальную модель формирования портфеля проектов, в которой оценки эффекта являются нечеткими, а оценки затрат ресурсов - четкими (последние также можно сделать нечеткими, однако это сделает модель слишком громоздкой). Пусть проект i ∈N по критерию l ∈K характеризуется нечеткой оценкой ай, определяемой функцией принадлежности ^(вй):Л^[0;1]. В силу аддитивности оценок эффекта, портфель Q ⊆N характеризуется векторной оценкой a~Q =(a~Q1, a~Q2, …, a~Qk), где a~Q1 - нечеткая оценка с функцией принадлежности µa~ (aQl): A l → [0; 1], вычисляемой (в силу принципа соответст- Ql Ql вия [127]) следующим образом: (2) >%(ое') = sup Вектор ресурсов для портфеля вычисляется также как и выше. В остальном алгоритм, описанный выше для четкого случая, остается без изменений (если носители нечетких множеств оценок пересекаются, то необходимо рассматривать обе комбинации, приведшие к одному и тому же значению). Отметим аддитивность процедуры (2) вычисления значений функций принадлежности, то есть Определим четкое множество (критериальное пространство) A'= ∏Al и предположим, что стратегические цели организации описываются нечеткой целью в этом пространстве. Функцию принадлежности нечеткой цели обозначим µ~(a), а = (a а2,..., ak)∈A'. Функцию принадлежности векторной нечеткой оценки a~Q портфеля Q в пространстве A' определим в соответствии с [127] как (3) µa~Q(a) = min {µa~Ql(aQl)}. Степень соответствия портфеля Q нечеткой стратегической цели организации µ~ (a) определим как (4) F(Q) = max min [ ^ (а), цё (а) ], Q ⊆N Число F(Q), принимающее значения в интервале от нуля до единицы, можно считать степенью (четкой!) соответствия портфеля Q стратегическим целям организации. Эту характеристику можно вычислять на каждом из шагов описанного выше алгоритма, что сводит нечеткую задачу к четкой. Интервальная модель. Частным случаем нечеткой модели является интервальная модель, в которой функция принадлежности принимает значения либо ноль, либо единица. Интервальная оценка a) ili-го проекта по l-му критерию будет описываться интервалом [a−, a+]: [0,аае[аа;аа] Интервальная оценка a)Ql портфеля Q ⊆N по l-му критерию вычисляется следующим образом:
параллелепипед в про- странстве A', соответствующий интервальным оценкам a)Ql,l∈K, портфеля Q. Тогда степень соответствия интервально оцениваемого портфеля Q нечеткой стратегической цели µ ~ (a) организации можно вычислить как = max µG~(a), Приведем иллюстративный пример. Пример формирования портфеля проектов Пусть имеются четыре проекта, характеристики которых заданы таблицей 6 (каждый проект оценивается по двум критериям). Таблица 6 Характеристики проектов
Из 4 проектов возможно составить 16 различных портфелей проектов (16 = 24), перечисленных в таблице 7. Нулевое значение переменной xi соответствует невключению i-го проекта в портфель, единичное - включению. 92 Стратегической целью будем считать достижение критериальных оценок (a1*, a2*), где ах = а2 = 30. Обозначим d{-, •) - евклидово расстояние в 5R2, и в качестве степени достижения цели выберем "расстояние до идеальной точки" a* (отметим, что критерии, по которым оцениваются проекты, считаются "равнозначными"):
Таблица 7
Видно, что пятый, восьмой и двенадцатый портфели являются доминируемыми. Для остальных портфелей построим зависимость степени достижения цели от затрат, приведенную на рисунке (см. Рис. 11). 0,9 HQ)
5 6 Затраты 10 11 Рис. 11. Степень достижения цели оптимальным портфелем проектов в зависимости от затрат Прямая, проведенная методом наименьших квадратов: F (с) ≈ 0,075 с, свидетельствует, что проекты схожи по своим характеристикам - зависимость степени достижения цели от затрат не имеет резких скачков. Эта зависимость позволяет оценить затраты, необходимые для "гарантированного" достижения цели a*: эти затраты равны с* ≈ 13,3. Итак, проведенный анализ свидетельствует, что актуальной теоретической задачей является разработка моделей и методов распределения ресурса и определения времен начала реализации технологически зависимых и независимых проектов в процессе решения задачи формирования портфеля проектов. В рамках предложенной многокритериальной нечеткой модели формирования портфеля проектов формально определена степень соответствия портфеля проектов стратегическим целям организации. Разработанная модель обобщает на нечеткий и многокритериальный случай классическую "задачу о ранце" и допускает нахождение оптимального портфеля методом динамического программирования. ПЛАНИРОВАНИЕ ПРОЦЕССА РЕАЛИЗАЦИИ ПОРТФЕЛЯ ПРОЕКТОВ 2.3.1. Обзор существующих моделей и методов планирования проектов Понятие «план» имеет много значений и в него часто вкладывается различный смысл. План реализации проекта отличается от функциональных планов типа плана производства, плана материально-технического снабжения, финансового плана и т.д., так как носит в принципе комплексный характер, то есть содержит полную систему целей и задач, соответствующих им детальных работ и мероприятий, направленных на достижение основной цели (миссии) проекта. Сущность планирования процесса реализации портфеля проектов состоит в задании целей и способов их достижения на основе формирования комплекса работ (мероприятий, действий), которые должны быть выполнены, применении методов и средств реализации этих работ, увязки ресурсов, необходимых для их выполнения, согласовании действий организаций-участников проекта [1, 53, 137]. На этапе планирования определяются все необходимые параметры реализации проекта: продолжительность по каждому из контролируемых элементов проекта, потребность в трудовых, материально-технических и финансовых ресурсах, сроки поставки сырья, материалов, комплектующих и технологического оборудования, сроки и объемы привлечения подрядных организаций. Процессы и процедуры планирования проекта должны обеспечи- вать реализуемость проекта в заданные сроки с минимальной стоимостью, в рамках нормативных затрат ресурсов и с надлежащим качеством. В общем случае, задача планирования процесса реализации портфеля проектов сводится к планированию независимых (в общем случае) проектов, входящих в состав портфеля. Класс задач планирования проектов является достаточно разработанным и нашел широкое распространение в литературе. Задачи планирования решаются до начала реализации проекта и заключаются в определении на основании всей имеющейся на данный момент информации оптимальных плановых значений управляющих параметров и, соответственно, состояний проекта на весь планируемый период его реализации [80]. В [41] приведена следующая классификация механизмов планирования в организационных системах: • Механизмы распределения ресурса [10,27,42]; • Механизмы активной экспертизы [27,42,41, 127]; • Механизмы внутренних цен [41, 147]; • Конкурсные механизмы [27,41]; • Механизмы обмена [82]. Классификация и применение механизмов распределения ресурса в задачах управления портфелями проектов будет приведена ниже. Применение механизмов активной экспертизы в процессе планирования позволяет существенно повысить его эффективность. Суть механизмов активной экспертизы заключается в получении и обработке информации о ключевых характеристиках проекта и его окружающей среды от экспертов - специалистах в конкретных областях. Применение механизмов внутренних цен решает проблему перераспределения работ по проекту и результатов, полученных от реализации проектов (в общем случае они могут измеряться в денежном эквиваленте), между участниками проекта. Конкурсные механизмы применяются в основном при выборе участников (подрядчиков) проекта. Общая идея любого конкурса заключается в следующем [41] - претенденты упорядочиваются на основании имеющейся у них информации (как объективной, так и сообщаемой самими претендентами), затем победителем (или победителями) объявляется претендент, занявший первое место (или, соответственно, несколько первых мест - в зависимости от условий конкурса). Возникающая при этом проблема заключается в том, что участники конкурса могут искажать сообщаемую информацию, то есть манипулировать ею с целю войти в число победителей. Именно для снижения негативной тенденции манипулирования информацией в процессе планирования проектов и применяются конкурсные механизмы. Существенный интерес представляет задача обмена ресурсами в рамках системы управления проектами. В данном случае задача заключается [41] в совершении наиболее выгодного для центра обмена ресурсов с агентами. Данный тип задач решается путем применения механизмов обмена. Также важным классом задач планирования проектов является его финансовое планирование. В [42] приведены следующие механизмы финансирования проектов: • Механизмы смешанного финансирования и кредитова- ния; • Механизмы страхования; • Механизмы самоокупаемости1; • Противозатратные механизмы. Механизмы смешанного финансирования и кредитования применяются при реализации крупномасштабных инвестиционных проектов, когда финансирование проекта из одного источника невозможно из-за его масштабности. В таких случаях региональных бюджетов бывает недостаточно для финансирования проектов
и необходимо привлекать частных инвесторов путем предоставления разного рода льгот (льготные условия работы в регионе, льготное кредитование, бюджетное финансирование и т.д.). Идея смешанного финансирования заключается в том, что бюджетные средства или льготный кредит выдаются при условии, что компания-участник обязуется выделить на проект собственное финансирование. Механизмы страхования в первую очередь ориентированы на минимизацию воздействия неопределенных и случайных факторов на участников проекта и непосредственно проект. В любом проекте имеет место дилемма «риск-доходность», причем в проектах она приобретает существенный вес, так как любой проект в какой-то степени уникален. Одним из методов защиты от отрицательных последствий является применение механизмов страхования. И, наконец, противозатратные механизмы позволяют нивелировать степень влияния на результат проекта его участников-монополистов. Противозатратными механизманми называются механизмы, побуждающие каждого участника максимально повышать эффективность своей деятельности. Перейдем теперь к рассмотрению одной из задач финансового планирования проекта. В данную модель включен параметр налогообложения проекта, являющийся существенным при реализации некоторых проектов, и учитываются моменты выплат налоговых платежей и заемные средства, необходимые для реализации проекта. 2.3.2. Описание модели планирования проектов портфеля с учетом параметров налогообложения Рассмотрим следующую модель1 управления портфелем проектов, учитывающую возможность оптимизации налоговых отчислений. Обозначим:
R0 - собственные средства на момент начала реализации портфеля (t = 0)(руб.). R - заемные средства на момент начала реализации портфеля (t = 0)(руб.). ti - время начала i-го проекта. г. - продолжительность i-го проекта (мес.). 8 - ставка налога на прибыль. с,-(τi) - затраты на реализацию i-го проекта (руб.). di (τi) - выручка от реализации i-го проекта (руб.). £ - дисконтирующий множитель (ставка кредита).
Т = max{ti +τi} - время завершения (длительность) портфеля i (мес.).
T0 ÷T К - кварталы, где K = .3. Для простоты в настоящей модели будем считать, что имеется единственный налог - налог на прибыль, который начисляется в момент завершения i-го проекта и уплачивается поквартально (по всем проектам, завершенным в данном квартале). Налог на прибыль уплачивается инвестором в порядке, установленном законодательством Российской Федерации, с учетом следующих особенностей: объектом обложения этим налогом является часть прибыльной продукции, принадлежащей инвестору. При этом такая стоимость уменьшается на сумму платежей инвестора за пользование заемными средствами, разовых платежей инвестора при пользовании недрами, а также на сумму других не возмещаемых инвестору затрат, состав и порядок учета которых при определении объекта обложения налогом на прибыль устанав- ливаются в соответствии с законодательством Российской Федерации. В случае, если указанные затраты превышают стоимость принадлежащей инвестору части прибыльной продукции, в последующие периоды объект обложения налогом на прибыль уменьшается на сумму, соответствующую возникающей разнице, до полного ее возмещения. В данном случае будем считать, что уплата налога на прибыль по проектам производится обособленно от уплаты налога на прибыль по другим видам деятельности. Также будем считать, что на реализацию портфеля проектов берется целевой кредит. Тогда можно считать, что R = 0 и учитывать в модели только параметр наличия собственных средств R0, в которые включен и размер целевого кредита. В указанных обозначениях, текущий финансовый баланс по портфелю проектов может быть представлен следующим образом: = R, хе~9 +fj{t>tt +Tl)xdt{Tt)xe-* - f/(t >г,.)хС((г,.)хе-* - =TJ+l)xI(t >tt +r,)xSx{{di{ri)-ci{ri))xe^,t e[(>,7]. В финансовый баланс по портфелю входят: А. Притоки - выручка от реализации продукции (услуг), получаемых в ходе реализации проектов портфеля, определяемая по конечной (реализуемой на сторону) продукции, прочие и внереализационные доходы, доходы (за вычетом налогов1) от реализации имущества и нематериальных активов (в частности при прекращении проекта), а также от возврата (в конце проекта) оборотных активов, уменьшение оборотного капитала на всех шагах расчетного периода; Б. Оттоки - вложения в основные средства на всех шагах расчетного периода, ликвидационные затраты, вложения средств
на депозит и в ценные бумаги других хозяйствующих субъектов, в увеличение оборотного капитала, компенсации (в конце проектов портфеля и портфеля в целом) оборотных пассивов. Эскиз графика финансового баланса представлен на рисунке (см. Рис. 12).
Рис. 12. Эскиз графика финансового баланса по портфелю проектов Если не учитывать условия неопределенности и риска реализации каждого отдельно взятого проекта, то достаточным (но не необходимым) условием финансовой реализуемости портфеля проектов является неотрицательность на каждом моменте времени реализации величины текущего финансового баланса по портфелю проектов. В указанных обозначениях, задача оптимизации рентабельности портфеля проектов может быть представлена следующим образом1: Ф(Т) > 0(T)>OVtc[O;T] То есть, в данной модели выбором моментов начала проектов портфеля и их продолжительности максимизируется рентабельность портфеля с учетом параметра налогообложения. При реализации того или иного портфеля проектов у руководства организации часто возникают вопросы, связанные с наличием денежных средств, необходимых для начала выполнения проектов, составляющих портфель, и сроках выполнения проектов -возможно ли завершить тот или иной проект раньше или задержать его выполнение, и как это скажется на финансовом состоянии портфеля. Поэтому им необходим инструмент прогноза наличия денежных средств и анализа изменения сроков выполнения проектов и соответственно интенсивности их выполнения на финансовую составляющую портфеля. Также, нельзя исключать из внимания вопрос равномерного распределения затрат по портфелю. Приведенная модель позволяет проведение укрупненного анализа финансовой составляющей портфеля по всем этим показателям с выделением параметра налогообложения, как параметра, оказывающего существенное влияние на реализуемость портфеля в тот или иной момент времени. С использованием описанной модели с той или иной степенью точности возможно решение следующих
проекта, i ∈ 1 …n, t- время начала j-го проекта, j ∈ 1 …n, ∆- задержка между началами i-го иj-го проекта. 102 типичных задач с необходимостью возникающих в ходе реализации практически каждого портфеля проектов: Задача 1. Прогнозирование наличия и движения денежных средств по портфелю проектов. При планировании любого проекта или портфеля проектов обязательно возникает вопрос «А реализуем ли проект/портфель при ограниченных ресурсах?». В каждой организации в качестве проектов/портфеля можно рассматривать и план реализации продукции (план продаж), и план производства, и план развития и т.д. Общим для них ресурсом являются финансы. В связи с этим возникает следующая задача. Задача 2. Проверка финансовой реализуемости портфеля. Если для реализации портфеля не хватает собственных средств, то необходимо заблаговременно определить, когда и сколько требуется заемных средств (на каждый отдельный временной отрезок портфеля и портфеля в целом). Отсутствие такой информации зачастую ведет к крупным финансовым потерям (например, неожиданно приходится брать кредит под большие проценты, или же наоборот, берутся лишние кредиты и т.д.) или же к приостановке или закрытию портфеля или части его проектов. Возникает следующая задача. Задача 3. Определение сроков и объемов необходимых заемных средств. Ответ на этот вопрос также можно получить на основании анализа текущего финансового баланса по портфелю проектов. Еще сложнее определить полезно или вредно использовать при реализации портфеля проектов заемные средства. В одних ситуациях это может существенно укрепить финансовое состояние портфеля и содействовать повышению его рентабельности. В других же ситуациях необходимость возврата кредита с процентами может привести к еще более острому дефициту, а может и к потерям. В худшем случае взятие кредита без предварительного анализа последствий может привести к «кредитной ловушке» и несостоятельности отдельных проектов и портфеля в целом. В связи с этим необходим инструмент для вариантного анализа и оценки последствий взятия заемных средств на различных условиях, и возникает Задача 4. Анализ целесообразности взятия заемных средств. В случае, если предлагаемый портфель все-таки остается финансово нереализуеым, необходимо его скорректировать, «урезав» требуемые финансовые средства (например, изменить технологию осуществления работ проектов, составляющих портфель, на более длительную, но менее затратную, заменить часть объектов на более дешевые объекты-аналоги и т.д.), и возникает вопрос: как нужно корректировать портфель, чтобы его новый вариант был реализуем при имеющихся ограничениях на финансы и в то же самое время был бы наиболее рентабельным. Возникает Задача 5. Формирование финансово реализуемого портфеля с минимальной упущенной прибылью. Также, для всех портфелей проектов характерна Задача 6. Определение срока окупаемости затрат, оценка прибыли за период реализации портфеля и создание его целевого плана. Одним из ключевых этапов жизненного цикла каждого проекта/портфеля является стадия его контроля. На этой стадии возникает Задача 7. Мониторинг и корректировка финансового плана портфеля и проектов, входящих в его состав, с учетом его фактического выполнения. Наряду с уже перечисленными задачами в организациях с проектно-ориентированной формой управления, часто возникает необходимость решения следующих задач: Задача 8. Построение и анализ консолидированного финансового баланса по нескольким портфелям или же по отдельным проектам, входящим в разные портфели, в разрезе различных критериев, характерных для каждой отдельно взятой организации. Задача 9. Разукрупнение, детализация консолидированного финансового баланса на группу финансовых балансов по объектам. Если смотреть на портфель с точки зрения налоговых выплат, то здесь возникают следующие задачи: Задача 10. Анализ влияния на динамику затрат по портфелю отдельно взятого налога. Задача 11. Анализ целесообразности применения методов налоговой оптимизации (изменение учетной политики по проекту, изменение структуры затрат по проекту и т.д.). В данной работе предпринята попытка объединения перечисленных задач в более укрупненные. Все приведенные задачи в той или иной степени включены ниже в три укрупненных группы задач. В выделенных группах все перечисленные задачи сознательно рассматриваются с «обособлением» налоговых выплат по проектам, составлюящим портфель, для проведения анализа их влияния на динамику текущего финансового баланса по портфелю. Также особое внимание уделяется анализу влияния изменения технологий на менее интенсивные, а значит и менее затратные, на динамику финансового состояния портфеля. 2.3.3. Модификации модели планирования портфеля проектов с учетом параметров налогообложения Итак, цель любой организации, реализующей портфель проектов, заключается в том, чтобы выполнить его в сжатые сроки и с минимальными затратами. Однако, цели минимизации времени реализации портфеля и минимизации затрат на его реализацию вступают в противоречие друг с другом. Поэтому для выявления множества рациональных вариантов (соотношения длительностей проектов, составляющих портфель, и затрат на их реализацию) целесообразно исследовать возможные комбинации времен реализации и затрат. Экстремальные их оценки могут быть получены в результате решения следующих групп задач. Группа 1. При заданных технологических зависимостях между проектами и критическими путями этих проектов, найти оптимальный размер собственных средств R0, необходимый для реализации портфеля. Необходимым условием реализации портфеля является неотрицательность текущего финансового баланса в любой момент реализации портфеля. В данной задаче длительность проектов τ, соответствует минимальному размеру затрат ci (τi) на их реализацию. Величина выручки, получаемой в результате реализации проекта di (τi) должна быть больше затрат на его реализацию и для каждого отдельного проекта является постоянной величиной (в данной задаче): Г R 0 → min J i0 ≥tj+∆ij,i,j = 1...n. L<p(o >o Группа 2. При заданных технологических зависимостях между проектами и оптимальной величиной собственных средств R0, найденном в группе задач 1, найти минимальную длительность портфеля, варьируя величину
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 983; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.180 (0.018 с.) |

 ; Будем считать, что чем выше оценка по каждом критерию, тем лучше.
; Будем считать, что чем выше оценка по каждом критерию, тем лучше. F)(Q) = 1- min d(a, a*) / (a1*)2 +(a2*)2, Q ⊆N Характеристики портфелей проектов приведены в таблице 7.
F)(Q) = 1- min d(a, a*) / (a1*)2 +(a2*)2, Q ⊆N Характеристики портфелей проектов приведены в таблице 7.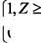 I(Z) - функция-индикатор I(Z) = <
I(Z) - функция-индикатор I(Z) = < ; В данной работе налоговые выплаты рассматриваются, как отдельная переменная с целью проведения анализа их влияния на совокупные затраты по проекту. 100
; В данной работе налоговые выплаты рассматриваются, как отдельная переменная с целью проведения анализа их влияния на совокупные затраты по проекту. 100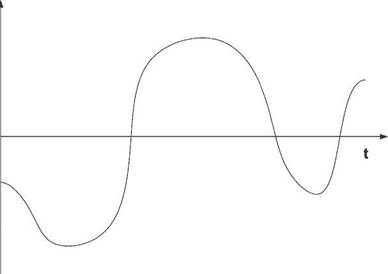
 ; Для простоты в настоящей модели будем рассматривать проекты с заданными технологическими зависимостями. Технологические ограничения по проектам задаются в следующем виде: ti ≥ tj + ∆ij, i,j = 1...n, где ti - время начала i-го
; Для простоты в настоящей модели будем рассматривать проекты с заданными технологическими зависимостями. Технологические ограничения по проектам задаются в следующем виде: ti ≥ tj + ∆ij, i,j = 1...n, где ti - время начала i-го


