
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формирование множества альтернативСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Множество S представляет собой совокупность альтернатив, удовлетворяющих в каждой задаче определенным ограничениям и рассматриваемых как возможные способы достижения поставленной цели. Если имеется только одна альтернатива, то проблемы принятия решений не возникает. Считают, что отсутствие многоальтернативности следует расценивать как недостаточную проработку решаемой проблемы. Универсальных методов формирования множества альтернатив не существует. Допустимые решения формируются на основе информации о реальной ситуации и имеющихся в задаче ограничений. Применяются так называемые качественные методы, т.е. методы направленные на активизацию использования интуиции и опыта ЛПР и экспертов. Например, множество альтернатив может быть сформировано на основе комбинаторно-морфологического анализа. Его суть заключается в том, что исходная проблема разбивается на ряд независимых подпроблем (уровней). Затем для каждого уровня определяются возможные способы решения подпроблемы (элемент уровня). Вариантом решения является набор элементов, в которых входит один элемент с каждого уровня. Например, если это объект проектирования, то он разбивается на функциональные блоки А, Б, В. Затем составляется морфологическая таблица (табл. 1.2.), каждая стока которой содержит возможные варианты одного из блоков объектов проектирования. Таблица 1.2
Варианты объекта образуют различные допустимые комбинации вариантов отдельных блоков (1-ая альтернатива - Кроме того, при формировании множества альтернатив может использоваться метод «коллективной генерации идей» (или метод «мозговой атаки»). Содержание метода заключается в следующем. Собирается группа лиц (главный принцип отбора - разнообразие профессий, квалификаций, опыта). Приветствуются любые идеи, возникающие как непроизвольно, так и по ассоциации при выслушивании предложений других участников, даже если они кажутся сомнительными или абсурдными. Категорически запрещается любая критика - важнейшее условие «мозгового штурма» (компетентную критику легче получить, чем компетентное творчество).
Формирование множества критериев Каждая альтернатива приводит к определенному исходу, последствия которого оцениваются по критериям 1. Признаются ЛПР в качестве характеристик степени достижения подцелей поставленной цели. 2. Являются общими и измеримыми для всех альтернатив. 3. Характеризуют общую ценность решения таким образом, что у ЛПР имеется стремление получить по ним наиболее предпочтительные оценки (т.е. они не могут быть представлены в виде ограничений). При формировании множества критериев руководствуются двумя принципами: - принципом полноты, - принципом простоты. Считается, что набор критериев является полным, если использование любых дополнительных критериев не изменяет результатов решения задачи, а отбрасывание хотя бы одного из выбранных критериев, наоборот, приводит к изменению результатов. Принцип простоты выражается в требованиях не избыточности (различные критерии из множества не должны учитывать один и тот же аспект последствий) и минимальности (множество должно содержать как можно меньше критериев). Критерии должны быть независимы, т.е. оценка альтернатив по одному из них не должна однозначно, либо с большой вероятностью, определять оценку по другому критерию. При большом количестве критериев их обычно объединяют в другие, т.е. выявление структуры критериев на множестве критериев. Формирование множества шкал Сравнение альтернатив удается провести лишь в том случае, если интенсивности свойств, определяемых выбранными критериями, могут быть измерены у всех альтернатив. Таким образом, возникает необходимость в разработке оценочных шкал критериев. Типы шкал и их основные характеристики приведены в табл. 1.3. Таблица 1.3
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1651; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.31.86 (0.007 с.) |




 ; 2-ая альтернатива -
; 2-ая альтернатива -  и т.д.).
и т.д.). . Критериями будем называть такие показатели, которые:
. Критериями будем называть такие показатели, которые: , либо
, либо  ;
- если
;
- если 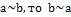 ;
- если
;
- если  , то
, то  .
Измерение состоит в том, чтобы проводимый эксперимент над объектом, определил принадлежность результата к тому или иному классу.
.
Измерение состоит в том, чтобы проводимый эксперимент над объектом, определил принадлежность результата к тому или иному классу.
 .
.
 b, либо b
b, либо b  ;
-
;
-  если a=b;
-
если a=b;
-  -
-  Эти шкалы могут иметь произвольные начала отсчета и единицы длины, а связь между показаниями в таких шкалах является линейной:
y=ax+b, a>0,
Эти шкалы могут иметь произвольные начала отсчета и единицы длины, а связь между показаниями в таких шкалах является линейной:
y=ax+b, a>0, 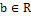 .
.
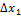 и
и  , а при другом выборе начала отсчета и единицы длины числами
, а при другом выборе начала отсчета и единицы длины числами  и
и  , то имеет место
, то имеет место  Примеры: температура (по Цельсию либо по Фаренгейту); время (у христиан от рождества Христова, у мусульман – Магомета) и т.п.
Примеры: температура (по Цельсию либо по Фаренгейту); время (у христиан от рождества Христова, у мусульман – Магомета) и т.п.
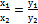 , т.е. y=ax
, т.е. y=ax 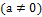 Примеры: длина, вес, электрическое сопротивление, деньги.
Примеры: длина, вес, электрическое сопротивление, деньги.



