
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнительный анализ парадигмСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лабораторная работа № 1 Методы принятия решений: смещенного идеала Цель работы: изучение основных алгоритмов методов смещенного идеала и метода перестановок.
Постановка задачи Провести ранжирование альтернатив в выбранной предметной области, методами смещенного идеала и методом перестановок. Альтернативы должны удовлетворять свойствам множества Эджворта-Парето. Матрица принятия решений 4х4. При определении важности критериев учитывать степень изменчивости их оценок. Сравнить полученные результаты.
Содержание отчета 1. Название и цель лабораторной работы. 2. Постановка задачи в соответствии предметной области. 3. Полученные результаты. Выводы. Контрольные вопросы 1. Анализ парадигм исследования операций и принятия решений (ПР). 2. Классификация типов проблем. 3. Что такое проблема, цель, тип задачи? 4. Альтернатива. Методы формирования множества альтернатив. 5. Критерии и ограничения. Принципы формирования множества критериев. 6. Основные типы шкал. Их характеристики. Аксиомы. 7. Методы оценки альтернатив. 8. Основные особенности выявления системы предпочтения личности, принимающей решения. 9. Концептуальная модель системы поддержки принятия решения. 10. Научно обоснованные методы принятия решений. Методы и требования, предъявляемые к ним. 11. Решающее правило. Множество Эджворта-Парето. 12. Общая схема решения многокритериальных задач ПР. Теоретические сведения Классификация типов проблем Существуют большие различия в природе изучаемых проблем принятия решения. Эти различия одним из первых заметил Г.Саймон, который предложил удачную классификацию проблем. Согласно этой классификации, проблемы подразделяются на три класса, т.е. в тех случаях, когда существуют адекватные математические модели устройств или процессов и есть опытные данные. 1. Хорошо структурированные или количественно сформулированные проблемы, в которых существенные зависимости выяснены настолько хорошо, что они могут быть выражены в числах или символах, получающих в конце концов численные оценки. 2. Неструктурированные или качественно выраженные проблемы, в которых известен только перечень основных параметров, но количественные связи между ними установить нельзя (нет необходимой информации). Иногда ясно лишь, что изменение параметра в определенных пределах сказывается на решении. В таких случаях структура, понимаемая как совокупность связей между параметрами не определена, и проблема называется неструктурированной. 3. Слабо структурированные или смешанные проблемы, которые содержат как качественные, так и количественные элементы, причем качественные малоизвестные и неопределенные стороны проблем имеют тенденцию доминировать. Согласно этой классификации типичные проблемы ИО можно назвать хорошо структурированными, т.е. существуют реальности допускающие строгое количественно описание и определяющие существование единственного очевидного критерия качества. Изучение реальной ситуации может требовать большого труда и времени. Необходимая информация может быть дорогостоящей. Метод «стоимость – эффективность» представляет собой первые попытки сравнения вариантов решений для слабо структурированных проблем. Типичные неструктурированные проблемы: проблема выбора профессии, конкурсного отбора проектов, выработки политики отбора статей в журналах, тендер. Слабоструктурированные и неструктурированные проблемы исследуются в рамках научного направления, называемого принятием решений при многих критериях.
Основные элементы многокритериальной задачи принятия решений Многокритериальная модель задачи принятия решений (ПР) может быть формально представлена в виде кортежа: <T, S, K, X, F, P, R>, где T – анализ проблемной ситуации и выявление целей и определение типа задачи, S – множество альтернатив, K – множество критериев, X – множество шкал, F – отображение множества альтернатив на векторных оценок, P – система предпочтений ЛПР, R – решающее правило. Формирование множества шкал Сравнение альтернатив удается провести лишь в том случае, если интенсивности свойств, определяемых выбранными критериями, могут быть измерены у всех альтернатив. Таким образом, возникает необходимость в разработке оценочных шкал критериев. Типы шкал и их основные характеристики приведены в табл. 1.3. Таблица 1.3
Построение решающих правил Решающее правило представляет собой принцип сравнения векторных оценок и вынесение суждений о предпочтительности одних по отношению к другим. Оно может быть задано в виде аналитического выражения, алгоритма или словесной формулировки. Упорядочение множества А с помощью некоторого решающего правила и использование свойств отображения F позволяет осуществить переход к упорядочиванию непосредственно альтернатив на множестве S. Решающие правила, используемые в многокритериальных задачах, можно разделить на: - эвристические; - аксиоматические. При эвристическом подходе решающее правило представляет собой способ свертывания критериев. При этом возникает необходимость в определении некоторых параметров свертки, которые несут информацию о важности критерия (т.е. о компромиссе между критериями). Аксиоматический подход основан на использовании теории полезности, авторами которой являются Д.Нейман и Д. Моргенштерн. Его отличают строгость, высокая точность в смысле малой вероятности ошибок. Но этот подход предполагает хорошее знание ЛПР решаемой задачи. ЛПР должен обладать четкой структурой предпочтений. Это более трудоемкая группа методов.
Требования и ограничения.
В итоге 70-х годов появился новый класс систем – системы поддержки принятие решений (СППР). Круг практического применения СППР стремительно расширяется. Это обусловлено следующими причинами: - пройден определённый этап в использовании вычислительных машин в задачах организационного управления; стали явнее причины провалов и неудач АСУ, которые использовались для обеспечения потребности руководителей; - накопились свидетельства о малом использовании классических моделей исследования операций в задачах принятия решений; пришло осознание того, что следует создать программные системы, ориентированные не на автоматизацию функций ЛПР, а на предоставление ему помощи в поисках хорошего решения; - появились результаты психологического исследования ЛПР принятия решений, но выяснилось, что человеческая система переработки информации ограничена, ему надо помогать специальным образом, организуя процесс принятия решений. СППР является интерактивной системой, которая позволяет ЛПР использовать данные, знания, объективные и субъективные модели для анализа и решения слабоструктурированных и неструктурированных проблем. Концептуальная схема СППР приведена на рис. 1.4.
Рис. 1.4
Блок АП: структуризация проблемы, проведение настройки СППР на предметной области пользователя (сформулировав множество критериев, альтернатив, множество шкал). Блок ПР: на входе поступает структурированная проблема, с другой стороны определяется тип задачи ПР, а также выбор решающего правила. Блоки БД, БМ, БЗ осуществляют поддержку блоков АП и ПР. Требования: корректные и научно-обоснованные методы должны удовлетворять: 1. В методе должны использоваться только такие способы получения информации от ЛПР и экспертов, которые соответствуют возможностям человеческой системы переработки информации. 2. В методах ПР должны быть предусмотрены средства проверки информации на непротиворечивость. Мы будем использовать алгоритм с использование основного правила логического вывода. A, B, C – альтернативы. 3. Любые соответствия между вариантами решений должны объясняться на основе информации, полученной только от ЛПР. 4. Любые допущения относительно решающего правила должны быть математически обоснованы. Ограничения. Следует подчеркнуть слово «поддержка». СППР только помогает принять решение, но они никогда не смогут заменить творчески мыслящего руководителя.
Множество Эджворта-Парето Определение. Альтернатива A доминирует над альтернативой B если:
Определение. Множество недоминируемых альтернатив является множеством Эджворта-Парето. Выделение множеств Эджворта-Парето является первым этапом решения задачи выбора.
Метод смещенного идеала Эта целая группа методов, которые отличает следующие особенности: - формирование идеального объекта, который в общем случае не принадлежит множеству альтернатив. - наличие процедуры отсеивания, т.е. исключения из исходного множества альтернатив худших. Полезность – воображаемая мера психологической и потребительской ценности различных благ. Дано:
1. Формирование идеального и неидеального объекта
Для мажорируемых критериев:
где Для минорируемых критериве:
где | 2. Переход к относительным единицам
3. Выявление системы предпочтения ЛПР
Чем
4. Определение расстояния, текущего i объекта до неидеального объекта с использованием меры Минковского
где p = 1, 2, 3, 4, 5. Для того, чтобы оба сомножителя 5. Упорядочивание альтернатив при различных заданиях параметра. Обычно Р = Например: S={
P=1 P=2 P=3 P=4 P=5
6. Процедура отсеивания, суть которой заключается в исключении из множества S альтернативы, которая наиболее часто находится на последнем месте (в рассмотренном примере это 7. Алгоритм повторяется начиная с первого шага, до тех пор, пока множество S не станет пустым. Преимущества: - метод работает при большом количестве объектов и критериев, т.е. полиномиальная сложность. Недостатки: - сложная операция для ЛПР оценки возможности критериев числовыми значениями; - шкалы критериев должны быть количественными; - результат получен в ранговой шкале.
С применением энтропии
1. Сформируем матрицу принятия решений
2. Проведем нормировку P =>
где i = 0≤ 3. Определим уровень энтропии
4. Уровень изменчивости
5. Определим
6. Если имеется экспертная оценка
Пример выполнения лабораторной работы Лабораторная работа №1 Методы принятия решений: «смещённого идеала» и перестановок
Цель работы: изучение основных алгоритмов метода «смещённого идеала» и перестановок. Постановка задачи: провести ранжирование альтернатив выбранной предметной области методом «смещённого идеала» и методом перестановок. Предварительно сформировать множество Эджворта-Парето. Матрица принятия решений – 4x4. При определении важности критериев учитывать степень изменчивости их оценок. Сравнить полученные результаты. Содержание отчёта 1. Назначение и цель лабораторной работы. 2. Постановка задачи в соответствующей предметной области. 3. Полученные результаты. Выводы. Пример выполнения Предметная область – пылесосы. Критерии – мощность, ёмкость пылесборника – мажорируемые, вес, цена – минорируемые. Альтернативы: 1. Bosch BSG 82425; 2. Electrolux Z 8810 UltraOne; 3. Samsung SC6530; 4. Zelmer Aquawelt 919.0 ST. Исходные данные
Альтернативы соответствуют множеству Эджворта-Парето. Важность критериев (экспертная оценка)
Шаг №1. Матрица принятия решений (x):
1. Идеальный и неидеальный объекты:
2. Переход к относительным единицам (d):
3. Определение комплексной важности: А) Матрица принятия решений:
Б) Нормированная матрица принятия решений (p):
В) Энтропия (Е):
Г) Инвертированная энтропия (l):
Д) Комплексная важность (
P1: S1>S3>S2>S4 P2: S1>S3>S2>S4 P3: S1>S3>S2>S4 P4: S1>S3>S2>S4 P5: S1>S3>S2>S4 Найдена наихудшая альтернатива – S4. Исключаем её. Шаг №2. Матрица принятия решений (x):
1) Идеальный и неидеальный объекты:
2) Переход к относительным единицам (d):
3) Определение комплексной важности:
А) Матрица принятия решений:
Б) Нормированная матрица принятия решений (p):
В) Энтропия (Е):
Г) Инвертированная энтропия (l):
Д) Комплексная важность (
4) Определение расстояния от неидеального объекта до i-го:
5) Ранжирование альтернатив и отсеивание: P1: S1>S3>S2 P2: S1>S3>S2 P3: S1>S3>S2 P4: S1>S3>S2 P5: S1>S3>S2 Найдена наихудшая альтернатива – S2. Исключаем её.
Шаг №3. Матрица принятия решений (x):
1) Идеальный и неидеальный объекты:
2) Переход к относительным единицам (d):
3) Определение комплексной важности: А) Матрица принятия решений:
Б) Нормированная матрица принятия решений (p):
В) Энтропия (Е):
Г) Инвертированная энтропия (l):
Д) Комплексная важность (
4) Определение расстояния от неидеального объекта до i-го:
5) Ранжирование альтернатив и отсеивание: P1: S1>S3 P2: S1>S3 P3: S1>S3 P4: S1>S3 P5: S1>S3 Найдена наихудшая альтернатива – S3. Исключаем её. Результат – альтернатива №1 – Bosch BSG 82425.
Метод перестановок Матрица принятия решений (x):
Комплексная важность (
Для перестановки {S1 S2 S3 S4} 1) S1>S2 C=(1 2 3) H=(4) 2) S1>S3 C=(1 2) H=(3 4) 3) S1>S4 C=(1 2 4) H=(3) 4) S2>S3 C=(1) H=(2 3 4) 5) S2>S4 C=(1 4) H=(2 3) 6) S3>S4 C=(3 4) H=(1 2) Вес перестановки: B=1,22314
Веса всех перестановок:
Лучшая перестановка (с максимальным весом) – 1324. Получаем лучшую альтернативу S1 – Bosch BSG 82425. Лабораторная работа № 2
Постановка задачи Провести оценку альтернатив при рассмотрении проблемы выбранной предметной области. Количество уровней – 3. Количество критериев не менее 5. Количество альтернатив не менее 3.
Содержание отчета
Контрольные вопросы 1. Методологические основы АИП. 2. Принципы и аксиомы АИП. 3. Определение иерархии и её формализация. 4. Шкала парных сравнений. Требования к ней. Закон Вебера-Фехнера. 5. Основные соотношения для идеально-согласованной матрицы парных сравнений (МПС). 6. Формулировка задачи обработки реальной МПС. 7. Содержательное отличие между индексом согласованности (ИС) и относительной согласованностью (ОС) 8. Принцип иерархической композиции. Локальные и глобальные приоритеты. Теоретические сведения Задачи принятия решений остро стоят перед: работниками управ- ления, экономистами, финансистами, социологами, оценщиками, работниками здравоохранения, военными, психологами, работниками социальной сферы, которые всегда стоят перед выбором наилучшего, наиболее нерискованного, дешевого решения. Система поддержки принятия решений на основе АИП может использоваться при решении следующих типовых задач: - оценка качества организационных, проектных и конструкторских решений; - определение политики инвестиций в различных областях; - задачи размещения (выбор места расположения вредных и опасных производств, пунктов обслуживания); - распределение ресурсов; - анализ рисков; - проведение анализа проблемы по методу «стоимость – эффективность»; - планирование от достигнутого и планирование желаемого будущего; - стратегическое планирование; - разрешение конфликтов; - проектирование и выбор оборудования, товаров; - выбор профессии, места работы, подбор кадров; - оценка рейтинга клиентов. Существуют многочисленные ссылки на успешное применение метода при решении разнообразных задач: - http://decisionlens.com/ - http://expertchoice.com/ Основные положения метода анализа иерархий были разработаны известным американским математиком Т. Л. Саати и опубликованы в 1977 г. Томас Саати является одним из самых ярких представителей прикладной науки. Об этом говорят не только математическая эрудиция и глубина новых теоретических результатов, но и диапазон приложений. Он был прав, предпослав к одной из своих монографий эпиграф: «Я люблю обе стороны математики: чистую – как возвышенный уход от реальности, прикладную – как страстное стремление к жизни». АИП используется для решения слабо структурированных и неструктурированных проблем. Методология решения таких проблем опирается на системных подход, при котором проблема рассматривается как результат взаимодействия множества разнородных объектов, а не просто как их изолированная и автономная совокупность. Человеку присущи два характерных признака аналитического мышления: один – умение наблюдать и анализировать наблюдения (т.е. разбить проблему в целом на составляющие части, более доступные для решения), другой – способность устанавливать отношения между частями, оценивая уровень (интенсивность) взаимосвязей, а затем синтезировать эти отношения в общее восприятие наблюдаемого. На основе этих свойств человеческого мышления были сформулированы три принципа, реализация которых и является содержанием АИП: - принцип идентификации и декомпозиции; - принцип дискриминации и сравнительных суждений; - принцип синтеза. АИП фокусируется на достижении целей. Его использование приводит к «рациональным решениям» в соответствии со следующим определением. Рациональным решением называется решение, которое наилучшим образом достигает множества целей, поставленных ЛПР. Ключевой момент здесь является фокусирование на целях, а не на альтернативах или атрибутах. Прямой метод Рассмотрим алгоритм над идеально-согласованной матрицей т.к. результаты в этом случае известны
1. Определим среднее геометрическое каждой строки R
2. Вычислим сумму средних геометрических, полученных в п. 1
3. Разделим среднее геометрическое каждой строки R (п. 1) на значение, полученное в п. 2, т. е. получим нормированное значение собственного вектора.
Для получения 4. Определим сумму элементов для каждого столбца матрицы R
5. Определим скалярное произведение векторов, полученных в п. 3 и в п. 4., что соответствует максимальному собственному числу идеально согласованной матрицы R.
Итерационный метод Основан на теореме: Теорема. Для положительной квадратной матрицы R собственный вектор
,где k=1,2,3… - т.;
c – константа; t – знак транспонирования; Вычисление собственного вектора
где k = 1, 2, 3, … – номер итерации; С достаточной для практики точностью принимается В результате обработки матрицы получаем «локальные» приоритеты элементов группы по отношению к родителю.
Переменные состояния Каждый канонический сценарий описывает состояние системы. Чтобы их охарактеризовать используют список переменных, которые называются переменными состояния. Каждый из канонических сценариев может быть описан на языке изменения этих переменных под статус кво. Интенсивность изменений предлагается измерять с помощью шкалы разностей, представленной в табл. 2.7. Таблица 2.7.
Калибровка переменных состояний относительно контрастных сценариев на примере материального положения трудоспособного населения представлена в табл.2.8. Таблица 2.8.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1086; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.44.115 (0.014 с.) |

 , либо
, либо  ;
- если
;
- если 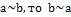 ;
- если
;
- если  , то
, то  .
Измерение состоит в том, чтобы проводимый эксперимент над объектом, определил принадлежность результата к тому или иному классу.
.
Измерение состоит в том, чтобы проводимый эксперимент над объектом, определил принадлежность результата к тому или иному классу.
 .
.
 b, либо b
b, либо b  ;
-
;
-  если a=b;
-
если a=b;
-  -
-  Эти шкалы могут иметь произвольные начала отсчета и единицы длины, а связь между показаниями в таких шкалах является линейной:
y=ax+b, a>0,
Эти шкалы могут иметь произвольные начала отсчета и единицы длины, а связь между показаниями в таких шкалах является линейной:
y=ax+b, a>0, 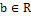 .
.
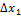 и
и  , а при другом выборе начала отсчета и единицы длины числами
, а при другом выборе начала отсчета и единицы длины числами  и
и  , то имеет место
, то имеет место  Примеры: температура (по Цельсию либо по Фаренгейту); время (у христиан от рождества Христова, у мусульман – Магомета) и т.п.
Примеры: температура (по Цельсию либо по Фаренгейту); время (у христиан от рождества Христова, у мусульман – Магомета) и т.п.
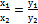 , т.е. y=ax
, т.е. y=ax 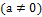 Примеры: длина, вес, электрическое сопротивление, деньги.
Примеры: длина, вес, электрическое сопротивление, деньги.

 .
. ,
, ,
, – оценка i-той альтернативы по j-му критерию.
– оценка i-той альтернативы по j-му критерию.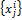 , где
, где  – матрица принятия решений (МПР).
– матрица принятия решений (МПР). ,
, .
. = max
= max 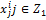 ,
, - подмножество мажорируемых критериев, то есть полезность объекта возрастает при возрастании оценки критериев.
- подмножество мажорируемых критериев, то есть полезность объекта возрастает при возрастании оценки критериев. = min
= min 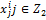 ,
, – подмножество минорируемых критериев, то есть полезность объекта возрастает при убывании оценки критериев
– подмножество минорируемых критериев, то есть полезность объекта возрастает при убывании оценки критериев | = m.
| = m. 0≤
0≤  ≤1.
≤1. .
.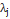 больше, тем важнее критерий
больше, тем важнее критерий
 ,
, были одинаково направлены, т.е. увеличивались
были одинаково направлены, т.е. увеличивались  соответственно вычисленному учету
соответственно вычисленному учету  при оценки объекта.
при оценки объекта. .
. }
}




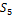 ).
).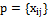
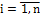
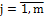
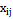 – оценка по j-ому критерию для i-ой альтернативы.
– оценка по j-ому критерию для i-ой альтернативы.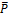
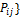
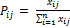 ,
, , j =
, j =  ,
, 
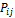 ≤1
≤1 для каждого критерия
для каждого критерия = -k
= -k 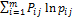 , где j=
, где j= 
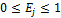
 =1-
=1-  , j=
, j=  , то комплексная важность критерия
, то комплексная важность критерия  , j=
, j=  ):
):
 ,
, 

 ,
,  выполним следующие шаги:
выполним следующие шаги: ,
, 

 , соответствующий максимальному собственному значению
, соответствующий максимальному собственному значению 
 - единичный вектор;
- единичный вектор; производятся до достижения заданной точности:
производятся до достижения заданной точности: ,
, – допустимая погрешность.
– допустимая погрешность.



