
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод принятия решения на основеСодержание книги
Поиск на нашем сайте
Аналитико-сетевого процесса (АСП)
Цель работы: Изучение основных этапов и алгоритмов метода анализа сетей. Постановка задачи
Привести оценку альтернатив при рассмотрении проблемы в виде сетевой структуры в выбранной предметной области. Количество кластеров не менее 3. Количество элементов в каждом кластере не менее 2-3. Представить суперматрицу структуры проблемы, затем взвешенную суперматрицу и предельные приоритеты элементов и кластеров. Содержание отчета 1. Название лабораторной работы. 2. Цель работы. 3. Постановка задачи в соответствующей предметной области. 4. Полученные результаты и выводы.
Контрольные вопросы 1. Различие и сходство между АИП и АСП. 2. Формализация первого этапа АСП. 3. Основные особенности, реализации второго этапа АСП. 4. Относительные и абсолютные приоритеты. 5. Сущность третьего этапа АСП. Что такое устойчивое предельное состояние системы? 6. Формулировка теоремы, используемой на этапе синтеза.
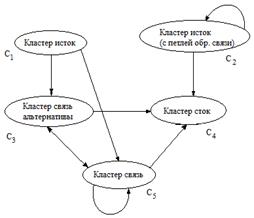
Теоретические сведения “Быть человеком означает принимать решения” – Т.Саати. Третья аксиома (принцип иерархической композиции) в АИП требует тщательной экспертизы, в отличии от первых двух. В задаче выбора приоритета альтернатив почти всегда зависят от элементов более высокого уровня, в то время как важность целей в действительности может зависеть от элементов нижнего уровня. Если это имеет место, то третья аксиома не применима. То есть в этом случае проблема описывается, где есть обратная связь, и поэтому они представляются в виде орграфа (сети) (рис.4.1).
Рис. 4.1
Обычно определяют приоритеты альтернатив, т.о. должен быть кластер, который объединяет альтернативы. Первый этап. Принцип идентификации и декомпозиции
На начальном этапе исследования должна быть четко сформулирована цель, в терминах которой будут определяться основные категории задачи: кластеры, элементы, суждения. Элементы задачи принятия решения объединяются в кластеры между которыми возможны произвольные связи, кластер имеет внешнюю зависимость, когда его элементы (или хотя бы один) связаны с элементами (которые тоже могут быть в единcтвенном числе) в другом кластере. Кластер может также иметь внутреннюю зависимость, когда его элементы связаны с другими элементами в том же кластере. Таким образом, кластеры в АСП, в общем случае, не являются простой совокупностью элементов. Если есть внутренняя зависимость, то имеет место свойство эммерджентность, т.е.
Формирование кластеров и связей является неформальной процедурой и осуществляется экспертами и ЛПР на основе конкретных знаний и специфики решаемой задачи. Результатом первого этапа будет граф, вершинами которого являются кластеры, а дуги отражают влияние кластеров друг на друга
i=< i.1; i.2; ….i.
где N – количество кластеров,
Рис. 4.2
Пример зависимости между кластерами – приход и уход материалов в отраслях промышленности. Электроэнергетическая промышленности снабжает электроэнергией другие отрасли промышленности, включая и себя.
Второй этап. Принцип дискриминации и сравнительных суждений Второй этап реализует принцип дискриминации и сравнительных суждений и заключается в построении МПС сначала для кластеров (макроуровень), а затем для элементов(микроуровень). Иерархии (которые используются в АИП) связаны с распределением качества критерия среди сравниваемых элементов, чтобы определить у какого из них количество данного критерия(качества) преобладает. Сети связаны с распределением влияния элементов, но некоторые элементы относительно данного качества(критерии), т.е. “влияние” является ключевым словом для АСП. Степень влияния кластеров друг на друга сводится к формированию матрицы размерности NxN. Заполнение ведется по столбцам. Таким образом для каждого столбца j матрицы V, кроме того случая, когда кластер j влияет на один кластер) может быть построена МПС, при заполнении которой эксперт отвечает на вопрос: “На какой из двух кластеров кластер j оказывает влияние больше?”. Следующий вопрос: ”Степень влияния (в соответствии с фундаментальной шкалой) относительно сформулированной цели”. Следующим этапом является формирование матриц парных сравнений для элементов кластеров и вычисление их приоритетов на основании которых формируется суперматрица размерностью MxM. Она состоит из блочных матриц.
Таблица 4.1
Таблица 4.2.
Рассмотрим как заполняется блок суперматрицы Во-первых, если j-ый кластер не влияет на i кластер, то блок размерностью Во-вторых, если влияет, то может быть два варианта: 1. Элемент 2. Если элемент j.m влияет, то в столбец j.m заносится веса влияния j.m m= После формирования суперматрицы получают взвешенную путем умножения каждой блочной матрицы
Сумма значений каждого столбца взвешенной суперматрицы
Третий этап. Этап синтеза Нас интересует приоритеты двух типов: показывающие влияние одного элемента на любой другой элемент в системе, известные как относительные приоритеты(это проделано во втором этапе), а также абсолютный приоритет любого элемента безотносительно того на какие элементы он влияет. Третий этап и определяет абсолютный приоритет, которые соответствуют устойчивому предельному состоянию системы с обратными связями. Определение этого состояния основывается на следующей теореме: Если
где Определение. Если матрица имеет единственный вектор, то матрица называется примитивной. Определение. Неотрицательная матрицы Столбец из матрицы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.233.69 (0.006 с.) |

 ,
,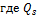 – свойство системы (целого) не является простой суммой свойств составляющих ее элементов (гостей)
– свойство системы (целого) не является простой суммой свойств составляющих ее элементов (гостей) 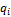 . В то же время свойства системы (целого) зависят от свойств составляющих ее элементов
. В то же время свойства системы (целого) зависят от свойств составляющих ее элементов .
.
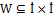
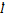 ={1,2,…,N}
={1,2,…,N}
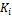 >,
>, - общее количество элементов.
- общее количество элементов.
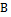 j-ом столбце указывает веса влияния j-го кластера полученного в результате обработки МПС на все остальные кластеры в соответствии с графом (полученном на первом этапа). Если кластер не влияет на какой-либо другой, то в матрицу
j-ом столбце указывает веса влияния j-го кластера полученного в результате обработки МПС на все остальные кластеры в соответствии с графом (полученном на первом этапа). Если кластер не влияет на какой-либо другой, то в матрицу  соответственно записывается значение ноль, если влияет только на один кластер то устанавливается единица.
соответственно записывается значение ноль, если влияет только на один кластер то устанавливается единица.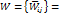
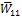
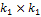

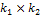
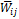
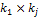

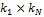
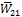
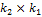
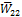
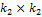
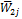
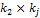
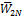
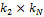




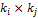
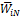

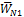
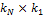
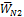
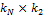

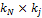

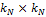



 . Заполнения ведутся также по столбцам.
. Заполнения ведутся также по столбцам.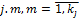 не влияет на элемент
не влияет на элемент  тогда столбец j.m заполняется нулями.
тогда столбец j.m заполняется нулями. элемента полученного в результате обработки МПС на элементы i.l.
элемента полученного в результате обработки МПС на элементы i.l. на коэффициент
на коэффициент  элемента матрицы V, т.е. такая нормировка суперматрицы обеспечивает свойство:
элемента матрицы V, т.е. такая нормировка суперматрицы обеспечивает свойство: ={
={ 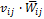 }
} 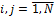
 k=1,2,….,
k=1,2,….,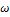 - матрица, имеющая одинаковые столбцы (единственный вектор равновесного состояния), элементы которых не изменяются при дальнейшем увеличении показателя степени.
- матрица, имеющая одинаковые столбцы (единственный вектор равновесного состояния), элементы которых не изменяются при дальнейшем увеличении показателя степени. является единичный вектор
является единичный вектор 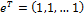 .
.


