
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип дискриминации и сравнительных сужденийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Данный принцип реализуется на втором этапе АИП. Суть его заключается в том, что, используя суждения ЛПР/эксперта и определенные алгоритмы их обработки, устанавливаются веса Суждения ЛПР/эксперта являются результатом исследования его структуры предпочтений. При этом исследовании применяется метод парных сравнений, содержание которого состоит в следующем. Пусть задано некоторое фиксированное множество объектов, которые сравниваются попарно с точки зрения их предпочтительности (желательности, важности, вероятности и т. д.).
Результаты записываются в виде матрицы парных сравнений
Результат сравнения отражает не только факт, но и степень предпочтения. При этом используется шкала парных сравнений. Выбор которой зависит от следующих требований: 1. Диапазон изменяемости шкалы должен соответствовать результатам когнитивной психологии. 2. Шкала должна давать возможность улавливать различия ощущения людей. Первая аксиома Саати: Если объекту i при сравнении с объектом j приписывается одна из целочисленных оценок, то действию j при сравнении с i приписывается обратное значение. Шкала парных сравнений (Фундаментальная шкала Саати) приведена в табл. 2.1 Таблица 2.1
Из шкалы следует свойство гомогенности (однородности) объектов. Это свойство соответствует способности людей сравнивать объекты, которые не слишком сильно отличаются друг от друга. Гомогенность существенна для сравнения объектов одного порядка, т. к. человеческий разум склонен к допущению больших ошибок при сравнении несопоставимых элементов. Когда эта несопоставимость большая, объекты располагаются в отдельные кластеры сравниваемых размеров, что выдвигает идею о создании необходимых уровней, т. е. дальнейшей декомпозиции. Суждения вне порядка величины обычно приводят к снижению точности и увеличению противоречивости. Это вторая аксиома Саати. Обоснование процедуры перевода результата парных сравнений, выраженных в качественной шкале в числовые значения, базируется на психо-физическом законе Вебера-Фехнера. Закон Вебера гласит, что различия в ощущениях становятся замеченными, когда значение стимула увеличивается не некоторый постоянный процент. Если S-значение стимула;
Причем закон справедлив, когда Фехнер сформулирован последовательности предельно значимых различий в стимулах, первый член которой обозначен
…
Таким образом, значимые различия в стимулах описывается геометрической прогрессией. Фехнер заметил, что соответствующие числам ощущения описываются арифметической прогрессией дискретных чисел. Их можно получить выразив n из последнего уравнения.
Если ощущения (реакцию) обозначить M, а S – значения стимула, то психофизический закон Вебера-Фехнера будет иметь вид
Положив b = 0 (колибровкой), определим
Разделим все Пример. Рассмотрим метод парных сравнений на примере покупки дома. Допустим необходимо оценить предпочтения ЛПР/эксперта на множестве вариантов A, B, C относительно критерия – размера дома. Лучше всего эту задачу свести к заполнению табл. 2.2. Размерность таблицы определяется количеством дуг, которые входят в рассматриваемую вершину. Элементы таблицы - какой из двух объектов предпочтительней? - какова степень предпочтительности? Таблица 2.2.
Таким же образом осуществляется оценка предпочтений ЛПР/эксперта относительно остальных критериев путем заполнения еще пяти аналогичных матриц размерностью 3x3. После чего метод парных сравнений распространяется на множество самих критериев относительно цели – покупки дома. В этом случае ЛПР/эксперту задается следующий вопрос: - какой из критериев для реализации цели наиболее важен? - в какой степени? В результате эксперимента получена матрица Формализацией понятия непротиворечивости для метода парных сравнений является выполнение следующего равенства:
Соотношение (1) соответствует правилу логического вывода: Если i объект предпочтительней объекта k на Теорема. Если матрица
R имеет rang = 1, а
или Практически добиться полной согласованности (т. е. непротиворечивости) суждений ЛПР/эксперта далеко не всегда возможно. Поэтому в общем случае Для дальнейшего анализа полезными являются следующие два факта из теории матриц: 1. Если Согласно этому утверждению, если имеет место (3) (т. е. матрица является идеально согласованной), то все собственные числа ее – нули, за исключением одного, равного n. 2. Если элемент положительной обратносимметричной матрицы R незначительно изменить, то все собственные числа этой матрицы также изменяется незначительно, т. е. они являются непрерывными функциями ее элементов. Объединяя эти результаты, находим, что при малых изменениях в Отсюда можно сформулировать следующую задачу: для нахождения весов дуг или объектов первого уровня по полученной в результате метода парных сравнений матрице R необходимо определить собственный вектор
Так как малые изменения в
Если Индекс согласованности матрицы парных сравнений, элементы которой сгенерированы случайным образом, называется случайным индексом (СИ). Ниже представлена табл. 2.3 соответствия порядка и среднего значения СИ, определенная на базе 100 случайных выборок.
Таблица 2.3
Отношение ИС к среднему СИ для матрицы того же порядка называется отношением согласованности (ОС):
Значение ОС меньшее или равное 10% считается приемлемым. Обычно ИС и ОС указываются в процентах. Согласно определению, ИС можно трактовать как отклонение от идеально проведенного эксперимента (метода парных сравнений), а ОС указывает, на сколько оцениваемая степень согласованности сходится со степенью согласованности самого неидеального случая. Таким образом, АИП допускает несогласованность (как неотъемлемую часть метода), признавая, что человеческие суждения находятся в постоянном процессе изменения и эволюции (поэтому не следует настаивать на 100% согласованности, так как суждения могут измениться после того как проблема решена). Но надежные решения не могут быть приняты без приемлемого уровня согласованности. Причины непротиворечивости: - ошибки служащих. Чаще всего вводится совсем не то, что подразумевалось; - недостаток информации. Если информация о сравниваемых факторах недостаточная или ее нет совсем, то его суждения будут случайными (вместо того, чтобы прерваться и потратить время и деньги на сбор дополнительной информации); - люди, принимающие решения утомлены или не заинтересованы в принятии данного решения; - реальный мир всегда противоречив. Реальный мир редко идеально последователен, иногда даже наоборот (например, спорт). Т. е. противоречия реального мира действительны. Вывод. Низкий уровень противоречивости не становится целью процесса ПР. Низкий уровень противоречивости необходим, но не достаточен для принятия хорошего решения. Можно быть идеально последовательным и в то же время последовательно неправым. Более важно быть достоверным, чем последовательным. Таким образом, между достоверностью и непротиворечивостью нет явной связи. Существует два метода решения уравнения 1. Прямой. 2. Итерационный.
Прямой метод Рассмотрим алгоритм над идеально-согласованной матрицей т.к. результаты в этом случае известны
1. Определим среднее геометрическое каждой строки R
2. Вычислим сумму средних геометрических, полученных в п. 1
3. Разделим среднее геометрическое каждой строки R (п. 1) на значение, полученное в п. 2, т. е. получим нормированное значение собственного вектора.
Для получения 4. Определим сумму элементов для каждого столбца матрицы R
5. Определим скалярное произведение векторов, полученных в п. 3 и в п. 4., что соответствует максимальному собственному числу идеально согласованной матрицы R.
Итерационный метод Основан на теореме: Теорема. Для положительной квадратной матрицы R собственный вектор
,где k=1,2,3… - т.;
c – константа; t – знак транспонирования; Вычисление собственного вектора
где k = 1, 2, 3, … – номер итерации; С достаточной для практики точностью принимается В результате обработки матрицы получаем «локальные» приоритеты элементов группы по отношению к родителю.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.012 с.) |

 дуг
дуг 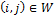 и веса
и веса 
 . Если на первом уровне один объект, то вес его принимается за 1.
. Если на первом уровне один объект, то вес его принимается за 1.
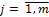 .
.
 .
. ,
,  , …,
, …,  -минимальная величина стимула, когда наши ощущения будут различать изменения в стимулах.
-минимальная величина стимула, когда наши ощущения будут различать изменения в стимулах.


 ;
; ;
;  =
= 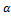
 ;
;

 , то
, то  (ощущений нет)
(ощущений нет)

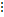

 на
на  . Мы получим последовательность абсолютных чисел фундаментальной шкалы Саати.
. Мы получим последовательность абсолютных чисел фундаментальной шкалы Саати. являются количественной оценкой интенсивности предпочтения i объекта, находящегося в i строке относительно j объекта, находящегося в j столбце, в соответствии с вышерассмотренной шкалой. При этом сравнении ЛПР/эксперту задаются два вопроса:
являются количественной оценкой интенсивности предпочтения i объекта, находящегося в i строке относительно j объекта, находящегося в j столбце, в соответствии с вышерассмотренной шкалой. При этом сравнении ЛПР/эксперту задаются два вопроса:


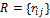 . Принимая во внимание свойство матрицы, т. е.
. Принимая во внимание свойство матрицы, т. е.  и, как следствие,
и, как следствие,  , количество вопросов равно:
, количество вопросов равно: 

 ,k (1)
,k (1) и k объект предпочтительней j объекта на
и k объект предпочтительней j объекта на  , то i объект должен быть предпочтительней j на
, то i объект должен быть предпочтительней j на  .
.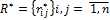 обладает свойством (1), то тогда существует такие числа
обладает свойством (1), то тогда существует такие числа 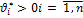 , что имеет место равенство:
, что имеет место равенство: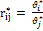
 (2)
(2) ,
,  является собственным вектором матрицы
является собственным вектором матрицы (3)
(3)
 будут отклоняться от «идеальных»
будут отклоняться от «идеальных»  являются собственными числами матрицы R и если
являются собственными числами матрицы R и если  .
. остается близким к n, остальные собственные значения остаются близкими к нулю.
остается близким к n, остальные собственные значения остаются близкими к нулю. , соответствующий максимальному собственному числу, т. е. решить уравнение
, соответствующий максимальному собственному числу, т. е. решить уравнение
 вызывают малое изменение
вызывают малое изменение 
 , то практически считается, что мера согласованности находится на приемлемом уровне.
, то практически считается, что мера согласованности находится на приемлемом уровне.

 ,
, 
 ,
,  ,
, 

 , соответствующий максимальному собственному значению
, соответствующий максимальному собственному значению 
 - единичный вектор;
- единичный вектор; производятся до достижения заданной точности:
производятся до достижения заданной точности: ,
, – допустимая погрешность.
– допустимая погрешность.



