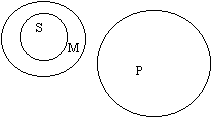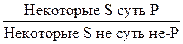Объединенная классификация простых суждений

ОБЪЕДИНЕННАЯ КЛАССИФИКАЦИЯ ПРОСТЫХ СУЖДЕНИЙ

Объединяя количественную и качественную характеристики, атрибутивные суждения делятся на четыре группы: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные.

Общеутвердительное – это суждение, общее по количеству и утвердительное по качеству. Напр., «Каждый, совершивший преступление, должен быть подвергнут справедливому наказанию». Схема такого суждения – «Все S суть Р», где кванторное слово «все» характеризует количество, утвердительная связка «суть» – качество суждения.

Общеотрицательное – суждение, общее по количеству и отрицательное по качеству. Напр., «Ни один невиновный не должен быть привлечен к уголовной ответственности». Схема такого суждения – «Ни одно S не есть Р». Кванторное слово «ни одно» характеризует количество, отрицательная связка «не есть» – качество суждения.

Частноутвердительное – суждение, частное по количеству и утвердительное по качеству. Напр., «Некоторые приговоры суда являются обвинительными». Схема такого суждения – «Некоторые S есть Р». Кванторное слово «некоторые» указывает на количество суждения, утвердительная связка, выраженная словом «есть», на его качество.

Частноотрицательное – суждение частное по количеству и отрицательное по качеству. Напр., «Некоторые приговоры суда не являются обвинительными». Схема такого суждения – «Некоторые S не есть Р». Кванторное слово «некоторые» указывает на количество суждения, отрицательная связка «не есть» – на его качество.

В логике принято сокращенное обозначение суждений по их объединенной классификации: А – общеутвердительные суждения; I – частноутвердительные; Е – общеотрицательные; О – частноотрицательные.

На языке логики предикатов рассмотренные суждения записывают следующим образом:

А – (Все S суть Р);

Е – (Ни одно S не есть Р);

I – (Некоторые S есть Р);

О – (Некоторые S не есть Р).

21) СЛОЖНЫЕ СУЖДЕНИЯ И ЕГО ВИДЫ

Сложным называют суждение, состоящее из нескольких про­стых, связанных логическими связками. Различают следующие виды сложных суждений: 1) соединительные, 2) разделительные, 3) услов­ные, 4) эквивалентные. Истинность таких сложных суждений опре­деляется истинностью составляющих их простых.

Соединительные (конъюнктивные) суждения.

Соединительным, или конъюнктивным называют суждение, со­стоящее из нескольких простых, связанных логической связкой «и».

В естественном языке конъюнктивная связка может быть пред­ставлена и такими выражениями, как: «а», «но», «а также», «как и», «хотя», «однако», «несмотря на», «одновременно» и другими.

Соединительное суждение может быть как двух-, так и многосо­ставным; в символической записи: р Ù q Ù r Ù… n. Приведем пример соединительного суждения, включающего более 20 конъюнктов:

В языке соединительное суждение может быть выражено одной из трех логико-грамматических структур.

1. Соединительная связка представлена в сложном субъекте по схеме: S и S₁ есть Р.

2) Связка представлена в сложном предикате по схеме: S есть P₁ и Р₂.

3) Связка представлена сочетанием первых двух способов по схеме: S и S₁ есть Р₁ и Р₂.

Соединительное суждение истинно при истинности всех состав­ляющих его конъюнктов и ложно при ложности хотя бы одного из них.

Разделительные (дизъюнктивные) суждения.

Разделительным, или дизъюнктивным, называют суждение, со­стоящее из нескольких простых, связанных логической связкой «или».

Разделительное суждение может быть как двух-, так и многосо­ставным: р Ú q Ú r Ú… n

В языке разделительное суждение может быть выражено одной из трех логико-грамматических структур.

1) Разделительная связка представлена в сложном субъекте по схеме: S₁ или S₂ есть Р.

2) Разделительная связка представлена в сложном предикате по схеме: S есть P₁ или P₂.

3) Разделительная связка представлена сочетанием первых двух способов по схеме: S₁ илиS₂ есть P₁ или P₂.

Нестрогая и строгая дизъюнкция. Поскольку связка «или» упот­ребляется в естественном языке в двух значениях — соединительно-разделительном и исключающе-разделительном, то следует разли­чать два типа разделительных суждений: 1) нестрогую (слабую) ди­зъюнкцию и 2) строгую (сильную) дизъюнкцию.

1) Нестрогая дизъюнкция — суждение, в котором связка «или» употребляется в соединительно-разделительном значении (сим­вол v).

2) Строгая дизъюнкция — суж­дение, в котором связка «или» упот­ребляется в разделительном значе­нии (символ).

Члены строгой дизъюнкции, называемые альтернативами, не могут быть одновременно истинными.

Разделительная связка в языке обычно выражается с помощью союзов «или», «либо». С целью усиления дизъюнкции до альтерна­тивного значения нередко употребляют удвоенные союзы: вместо выражения «р или q» употребляют «или р, или q», а вместе «р либо q» — «либо р, либо q».Поскольку в грамматике отсутствуют одно­значные союзы для нестрогого и строгого разделения, то вопрос о типе дизъюнкции в юридических и других текстах должен решаться содержательным анализом соответствующих суждений.

Полная и неполная дизъюнкция. Среди дизъюнктивных сужде­ний следует различать полную и неполную дизъюнкцию.

Полным или закрытым называют дизъюнктивное суждение, в котором перечислены все признаки или все виды определенного рода.

Символически это суждение можно записать следующим образом:

<р v q v r>.

Например: «Леса бывают лиственные, хвойные или смешанные». Полнота этого разделения (в символической записи обозначается знаком <...>) определяется тем, что не существует, помимо указанных, других видов лесов.

Неполным или открытым называют дизъюнктивное суждение, в котором перечислены не все признаки или не все виды определен­ного рода. В символической записи неполнота дизъюнкции может быть выражена многоточием:

р v q v r v...

В естественном языке не­полнота дизъюнкции выражается словами: «и т.д.», «и др.», «и тому подобное», «иные» и другими.

Отношения суждений по их истинностным значениям исследуются в логике между сравнимыми суждениями.

Несравнимые простые суждения имеют разные субъекты и предикаты, например: «Закон суров» и «Небо ясное». Истинность и ложность таких суждений не зависит друг от друга. Сравнимые простые суждения имеют одинаковые субъект и предикат (поэтому они и сравнимы по содержанию), но различаются количественными и качественными характеристиками логической формы. Несравнимые сложные суждения включают в себя полностью или частично разные по содержанию простые суждения. Например, суждения: «Прокуроры и следователи имеют юридическое образование» и «Прокуроры и следователи стоят на страже законности». Сравнимые сложные суждения включают одинаковые исходные простые суждения, а различаются типом связи между ними (т.е. логическими союзами). Например: «Кража и мошенничество строго караются по закону», «Кража или мошенничество строго караются по закону», «Неверно, что кража и мошенничество строго караются по закону».

Между сравнимыми суждениями выделяются два типа отношений: совместимость и несовместимость. Суждения рассматриваются как совместимые, если онимогут быть одновременно истинными, и как несовместимые, если они не могут быть одновременно истинными.

Совместимость бывает трех видов: эквивалентность, подчинение и частичная совместимость.

1. Суждения эквивалентны, если они всегда принимают одинаковые истинностные значения. Простые категорические суждения (А, Е, J, О) находятся в отношении эквивалентности, если они различны по количеству и качеству, и одно из них стоит под отрицанием: ~ А эквивалентно О («Неверно, что все юристы адвокаты» эквивалентно «Некоторые юристы не адвокаты»); ~ О эквивалентно А («Неверно, что некоторые адвокаты не юристы» эквивалентно «Все адвокаты юристы»); ~ J эквивалентно Е («Неверно, что некоторые студенты профессора» эквивалентно «Ни один студент не профессор»); ~ Е эквивалентно J («неверно, что ни один гриб не ядовит» эквивалентно «Некоторые грибы ядовиты»).

Сложные суждения находятся в отношении эквивалентности, когда при одних и тех же значениях истинности исходных простых суждений они принимают одинаковые значения. Это всегда можно установить построением истинностных таблиц для рассматриваемых сложных суждений.

2. Суждение находится в отношении подчинения к другому (подчиняющему), если оно истинно во всех тех случаях, когда истинно подчиняющее. Это отношение имеет место между простыми категорическим суждениями, у которых количество различно, а качество одно и то же. В таком отношении находятся: общеутвердительные (А) и частноутвердительные (J) суждения; общеотрицательные (Е) и частноотрицательные (О) суждения. Здесь действуют такиезакономерности: (1) из истинности общего (А или Е) следует соответственно истинность частного (J или О), но не наоборот; (2) из ложности частного (J или О) следует ложность общего (А или Е), но не наоборот. Например, если истинно «Все студенты нашей группы - успевающие» (А), то тем более истинно «Некоторыестуденты нашей группы успевающие» (J). В свою очередь, если ложно «Некоторые люди вправе нарушать закон» (J), то тем более ложно, что «Все люди вправе нарушать закон» (А).

Отношение подчинения в сложных суждениях имеет свойства логического следования, которое характеризуется тем, что при истинности подчиняющего суждения В подчиненное суждение С всегда истинно, и не может быть так, что суждение В истинно, а суждение С – ложно. Например: «Если у человека повышенная температура (В), то он болен (С)». При наличии температуры у человека (В) – истинно, следует с необходимостью истинность суждения (С). Но при ложности В, суждение С может быть как истинным, так и ложным.

Отношение частичной совместимости также имеет место как между простыми, так и сложными суждениями. Для этого отношения характерна следующая закономерность: невозможна совместная ложность суждений, находящихся в отношении частичной совместимости. В случае простых суждений – это отношение между суждениями одинакового количества, но разного качества: между частноутвердительными (J) и частноотрицательными (О) суждениями. Из ложности одного из них следует истинность другого, но не наоборот: из истинности одного из них не следует с необходимостью ложность другого – оно также может быть истинным. Эту закономерность особо следует учитывать в практике мышления. Так, при истинности (J) – «Некоторые следователи независимы» может быть истинным и (О) – «Некоторые следователи не являются независимыми». Но при ложности суждения (J) – «Некоторые следователи независимы» необходимо будет истинным противоположное по качеству суждение, т.е. (О) – «Некоторые следователи не являются независимыми».

Противоположность между суждениями проявляется в том, что данные суждения не могут быть вместе истинными, но могут быть вместе ложными. Для этого отношения характерна закономерность обратная той, которая характерна для отношения частичной совместимости: если одно из двух суждений истинно, то другое необходимо ложно, но при ложности одного из них другое может быть как истинным, так и ложным. Иными словами, возможна ложность обоих суждений.

В случае простых суждений, это отношение имеет место между общеутвердительными (А) и общеотрицательными (Е) суждениями. Так, если истинно (А) – «Все адвокаты – юристы», то ложно (Е) – «Ни один адвокат не юрист». Но если ложно (А) – «Все свидетели правдивы», то из него не следует истинность суждения (Е) – «Ни один свидетель не правдив», оно тоже ложно. Но в других случаях (Е) может быть истинным. Так, если ложно суждение (А) – «Все граждане вправе нарушать закон», то истинно (Е) – «Ни один гражданин не вправе нарушать закон».

Знание отношений между суждениями по их истинным значениям важно в познавательном и практическом планах, поскольку помогает избегать возможных ошибок в собственных рассуждениях, позволяет грамотно анализировать различные контексты, высказывания оппонентов. Часто встречаются ситуации, когда суждениями оперируют как исключающими друг друга. Например, когда кто-то выдвигает суждение в форме «Некоторые S есть Р», а другой - в форме «Некоторые S не есть Р». Логический же анализ этих суждений показывает, суждения, высказанные в такой форме, не исключают друг друга, а являются частично совместимыми, и оба могут оказаться истинными. Весьма часто также в споре из истинности частного суждения (J или О) выводят истинность общего (А или Е) соответственно, что нарушает правильность отношений между ними.

В дискуссии, споре, в частности по юридическим и экономическим вопросам, чтобы опровергнуть общее ложное суждение, часто используют противоположное ему общее суждение. Но так легко попасть впросак: оно тоже может оказаться ложным. В логическом отношении для точного опровержения достаточно привести противоречащее суждение (см. ниже схему логического квадрата). Смешение противоположных и противоречащих суждений довольно частая ошибка в практике мышления. Поэтому важно уметь осуществлять логический анализ отношений между суждениями.

Для осуществления логического анализа отношений между простыми суждениями используют графическую схему, называемую «логическим квадратом»: его вершины символизируют четыре вида простых категорических суждений – А, Е, J, О; стороны и диагонали – отношения между этими суждениями.

Чтобы определить отношение между простыми категорическими суждениями, нужно:

1. определить, какого вида эти суждения: А, Е, J, О;

2. найти соответствующие углы логического квадрата;

3. посмотреть какое отношение вписано между ними;

Правила терминов

1. В силлогизме должно быть только три термина (S, P, M). Нарушение этого правила ведёт к ошибке "учетверение терминов":

Движение (М) – вечно (Р)

Хождение в школу (S) – движение (М)

Хождение в школу вечно

В данном силлогизме средний термин "движение" употребляется в разных смыслах – в предельно широком (философском) и обыденном (движение как перемещение). Заключение ложно.

2. Средний термин должен быть распределён по крайней мере в одной из посылок.

Все гусеницы (Р) едят салат (М)

Я (S) ем салат (М)

Я – гусеница

Средний термин (те, кто едят салат) не распределён ни в одной из посылок. Вывод ложный.

3. Термин в заключении может быть распределён только тогда, когда он распределён в посылке.

Во всех городах за полярным кругом (М) – белые ночи (Р)

Санкт-Петербург (S) – не за полярным кругом (М)

В Санкт-Петербурге не бывает белых ночей.

Предикат вывода распределён в заключении, но не распределён в посылке. В терминах заключения говорится больше, чем в посылках: произошло расширение большего термина. Заключение ложно.

Правила посылок

1. Из двух отрицательных посылок вывод не производится.

Дельфины не рыбы.

Щуки не дельфины.

?

2. Если одна из посылок отрицательная, то и заключение должно быть отрицательным:

Некоторые люди не умеют читать.

Все люди умеют смеяться.

Некоторые из умеющих смеяться не умеют читать.

3. Из двух частных посылок нельзя сделать вывод:

Некоторые животные живут в воде.

Некоторые говорящие существа – животные.

?

4. Если одна из посылок частная, то заключение должно быть частным:

Все люди обладают сознанием.

Некоторые двуногие существа – люди.

Некоторые двуногие существа обладают сознанием.

Вывод А

Все М есть Р Все S есть М Все S есть Р   Все люди смертны Сократ – человек Сократ смертен

Вывод Е

Ни одно М не есть Р Все S есть М Ни одно S не есть Р   Ни одно дерево не летает Все берёзы – деревья Ни одна берёза не летает

Вывод I

Все М есть Р Некоторые S есть М Некоторые S есть Р   Все зебры – полосатые Некоторые лошади – зебры Некоторые лошади – полосатые

Вывод О

Ни одно М не есть Р Некоторые S есть М Некоторые S не есть Р   Ни одно растение не говорит Некоторые формы жизни – растения Некоторые формы жизни не говорят

Примеры ошибок:

а) Все студенты сдают экзамены, а некоторые водители не сдают экзаменов. Значит, некоторые водители – не студенты. Все Р есть М Некоторые S не есть М Некоторые S не есть Р

б) Некоторые студенты занимаются музыкой, а ни один попугай музыкой не занимается, следовательно некоторые попугаи не являются студентами. Некоторые Р есть М Ни одно S не есть М Некоторые S не есть Р

В обоих примерах вывод с необходимостью не следует из посылок, поскольку отношение субъекта и предиката в заключении не однозначно.

29) Непосредственным называется умозаключение, в котором вывод делается из одной посылки путем преобразования исходного суждения по форме при сохранении смысла.

Способы образования непосредственных умозаключений:

1) превращение;

2) обращение;

3) противопоставление предикату;

4) противопоставление субъекту;

5) ограничение третьего понятия;

6) умозаключение по логическому квадрату.

Превращение

Превращение – это такое непосредственное умозаключение, в котором устанавливается связь между понятием, являющимся субъектом исходного суждения, и понятием, противоречащим предикату исходного суждения.

Для превращения утвердительного суждения в отрицательное, при сохранении смысла исходного суждения вводят два отрицания, или наоборот: если исходное суждение отрицательно, то удаляют отрицание. Таким образом, во-первых, меняется связка исходного суждения на противоположную по качеству («есть» на «не есть», «суть» на «не суть», и наоборот), а, во-вторых, меняется качество предиката исходного суждения на противоположное («Р» на «не-Р», «не-Р» на «Р»).

· Общеутвердительное суждение (А), превращается в общеотрицательное (Е).

Например:

· Общеотрицательное суждение (Е) превращается в общеутвердительное (А).

Например:

· Частноутвердительное суждение (I) превращается в частноотрицательное (О).

Например:

· Частноотрицательное суждение (О) превращается в частноутвердительное (I).

Например:

Обращение

Обращение – это такое непосредственное умозаключение, при котором из данного суждения, – не являющегося частноотрицательным – выводится такое суждение, субъектом которого является предикат исходного, а предикатом – субъект исходного суждения.

В зависимости от распределенности терминов исходного суждения различают два вида обращения: чистое обращение и нечистое обращение.

1. Чистое (простое) обращение имеет место в том случае, если оба термина (субъект и предикат) исходного суждения являются распределенными или оба являются нераспределенными, то есть имеют одинаковые объемы.

· Общеотрицательное суждение (Е) обращается в общеотрицательное (Е):

Например:

· Частноутвердительное суждение (I) обращается в частноутвердительное (I):

Например:

2. Нечистое обращение представлено двумя вариантами: обращением с ограничением и обращением с приращением.

· Обращение с ограничением имеет место при переходе от общеутвердительных суждений (А) к частноутвердительным (I):

Например:

· Обращение с приращением имеет место в случае выделяющих суждений и связано с переходом от частных суждений к общим:

Например:

· Частноотрицательное суждение необращается.

Противопоставление субъекту

Противопоставление субъекту – это такое непосредственное умозаключение, в результате которого в заключении субъектом становится предикат исходного суждения, а предикатом – понятие, противоречащее субъекту исходного суждения. Противопоставление субъекту представляет собой последовательное применение обращения исходного суждения и далее превращения полученного при этом суждения.

· Противопоставление субъекту общеутвердительного суждения (A) дает частноотрицательное суждение (O):

Например:

· Противопоставление субъекту общеотрицательного суждения (E) дает общеутвердительное суждение (A):

Например:

· Противопоставление субъекту частноутвердительного суждения (I) дает частнотрицательное суждение (O):

Например:

· Противопоставление предикату частноотрицательного суждения (O) не возможно.

Понятие логической формы

Логической формой конкретной мысли является строение этой мысли, т.е. способ связи ее составных частей. Логическая фор­ма отражает объективный мир, но это отражение не всей полно­ты содержания мира, существующего вне нас, а его общих структурных связей, которые необходимо воплощаются и в стру­ктуре наших мыслей. Понятия, суждения, умозаключения име­ют свои специфические формы (структуры).

Структура мысли, т.е. ее логическую форму, можно выра­зить при помощи символов. Выявим структуру (логическую форму) трех следующих суждений: “Все караси - рыбы”, “Все люди смертны”, “Все бабочки - насекомые”. Содержание у них разное, а форма одна и та же: “Все S суть Р”; она включает S (субъект), т. е. понятие о предмете суждения, Р (предикат), т. е. понятие о признаке предмета, связку (“есть”, “суть”), кванторное слово (“все”). Иногда связка может отсутствовать или за­меняться на тире.

Два следующих условных суждения имеют одну и ту же форму:

1) “Если железо нагревать, то оно расширяется”;

2) “Если учащийся изучает логику, то он повышает четкость своего мышления”. Форма этих суждений такая: “Если S есть Р, то S есть Р1”.

Логические законы

Соблюдение законов логики - необходимое условие достиже­ния истины в процессе рассуждения. Основными формально-логи­ческими законами обычно считаются: 1) закон тождества; 2) за­кон непротиворечия, 3) закон исключенного третьего; 4) закон достаточного основания. Они будут подробно излагаться в отдельной главе. Эти законы (принципы) выражают определен­ность, непротиворечивость, доказательность мышления.

Логические принципы действуют независимо от воли людей, они не созданы по их воле и желанию, а являются отражением связей и отношений вещей материального мира. Общечеловече­скийхарактер принципов формальной логики состоит в том, что во все исторические эпохи все люди мыслили по одним и тем же логическим принципам. Кроме формально-логических принципов, правильное мышление подчиняется также основным законам диа­лектики: закону единства и борьбы противоположностей, закону взаимного перехода количественных и качественных изменений, закону отрицания отрицания.

Правила терминов

1. В силлогизме должно быть только три термина (S, P, M). Нарушение этого правила ведёт к ошибке "учетверение терминов":

Движение (М) – вечно (Р)

Хождение в школу (S) – движение (М)

Хождение в школу вечно

В данном силлогизме средний термин "движение" употребляется в разных смыслах – в предельно широком (философском) и обыденном (движение как перемещение). Заключение ложно.

2. Средний термин должен быть распределён по крайней мере в одной из посылок.

Все гусеницы (Р) едят салат (М)

Я (S) ем салат (М)

Я – гусеница

Средний термин (те, кто едят салат) не распределён ни в одной из посылок. Вывод ложный.

3. Термин в заключении может быть распределён только тогда, когда он распределён в посылке.

Во всех городах за полярным кругом (М) – белые ночи (Р)

Санкт-Петербург (S) – не за полярным кругом (М)

В Санкт-Петербурге не бывает белых ночей.

Предикат вывода распределён в заключении, но не распределён в посылке. В терминах заключения говорится больше, чем в посылках: произошло расширение большего термина. Заключение ложно.

Правила посылок

1. Из двух отрицательных посылок вывод не производится.

Дельфины не рыбы.

Щуки не дельфины.

?

2. Если одна из посылок отрицательная, то и заключение должно быть отрицательным:

Некоторые люди не умеют читать.

Все люди умеют смеяться.

Некоторые из умеющих смеяться не умеют читать.

3. Из двух частных посылок нельзя сделать вывод:

Некоторые животные живут в воде.

Некоторые говорящие существа – животные.

?

4. Если одна из посылок частная, то заключение должно быть частным:

Все люди обладают сознанием.

Некоторые двуногие существа – люди.

Некоторые двуногие существа обладают сознанием.

Вывод А

Все М есть Р Все S есть М Все S есть Р   Все люди смертны Сократ – человек Сократ смертен

Вывод Е

Ни одно М не есть Р Все S есть М Ни одно S не есть Р   Ни одно дерево не летает Все берёзы – деревья Ни одна берёза не летает

Вывод I

Все М есть Р Некоторые S есть М Некоторые S есть Р   Все зебры – полосатые Некоторые лошади – зебры Некоторые лошади – полосатые

Вывод О

Ни одно М не есть Р Некоторые S есть М Некоторые S не есть Р   Ни одно растение не говорит Некоторые формы жизни – растения Некоторые формы жизни не говорят

Примеры ошибок:

а) Все студенты сдают экзамены, а некоторые водители не сдают экзаменов. Значит, некоторые водители – не студенты. Все Р есть М Некоторые S не есть М Некоторые S не есть Р

б) Некоторые студенты занимаются музыкой, а ни один попугай музыкой не занимается, следовательно некоторые попугаи не являются студентами. Некоторые Р есть М Ни одно S не есть М Некоторые S не есть Р

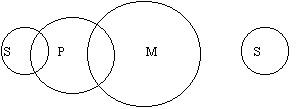
В обоих примерах вывод с необходимостью не следует из посылок, поскольку отношение субъекта и предиката в заключении не однозначно.

34) Фигуры и модусы простого категорического силлогизма

Фигурами категорического силлогизма называются формы силлогизма, различающиеся по положению среднего термина (М) в посылках. Имеется четыре фигуры категорического силлогизма:

I-ая фигура

Все злаки (М) – растения (Р) Рожь (S) – злак (М) Рожь (S) – растение (P)

II-ая фигура.

Все ужи (Р) – пресмыкающиеся (М) Это животное (S) – не пресмыкающееся (М) Это животное (S) – не уж (Р)

III-я фигура.

Все углероды (М) – простые тела (Р) Все углероды (М) – электропроводники (S) Некоторые электропроводники (S) – простые тела (Р)

IV-ая фигура.

Все киты (Р) – млекопитающие (М) Ни одно млекопитающее (М) – не рыба (S) Ни одна рыба (S) – не кит (Р)

Каждая фигура категорического силлогизма имеет свои особые правила:

I фигура:	Большая посылка – общая, меньшая посылка – утвердительная.
II фигура:	Большая посылка – общая, одна из посылок – отрицательная.
III фигура:	Меньшая посылка – утвердительная, заключение – частное.
IV фигура:	Заключение не может быть общеутвердительным суждением.

В каждой фигуре возможно несколько допустимых (правильных) сочетаний посылок и заключения. Такие сочетания называются модусами.

Модусы фигур категорического силлогизма – разновидности силлогизма, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключений.

Всего в фигурах силлогизма 19 правильных модусов. Каждому модусу присвоено латинское название, в котором гласные буквы последовательно обозначают вид суждений большей посылки, меньшей посылки и заключения.

I фигура:	Barbara, Celarent, Darii, Ferio; ААА, ЕАЕ, АII, ЕIО.
II фигура:	Cezare, Camestres, Festino, Baroko; ЕАЕ, АЕЕ, ЕIО АОО;
III фигура:	Darapti, Disamis, Datisi, Felapton, Вocardo, Ferison; ААI, IАI, АII, ЕАО, ОАО, ЕIО.
IV фигура:	Bramantip, Camenes, Dimaris, Fesapo, Fresison; ААI, АЕЕ, IАI, ЕАО, ЕIО.

Чтобы получить истинное заключение в силлогизме, необходимо брать истинные посылки, соблюдать правила фигур и не нарушать общие правила простого категорического силлогизма.

35) Умозаключение, посылки и заключение которого являются суждени­ями с отношениями, называется умозаключением с отношениями.

Например:

Петр — брат Ивана. Иван — брат Сергея.

Петр — брат Сергея.

Посылки и заключение в приведенном примере — суждения с от­ношениями, имеющие логическую структуру xRy, где х и у — понятия о предметах, R — отношения между ними.

Логическим основанием умозаключений из суждений с отноше­ниями являются свойства отношений, важнейшие из которых — 1) симметричность, 2) рефлексивность и 3) транзитивность.

1. Отношение называется симметричным (от греческого simmetria—«соразмерность»), если оно имеет место как между предметами х и у, так и между предметами у и х. Иначе говоря, перестановка членов отношения не ведет к изменению вида отношения. Симметричными являются отношения равенства (если а равно Ь, то и b равно а), сходства (если с сходно с d, то и d сходно с с ), одновременности (если событие х произошло одновременно с событием у, значит, и событие у произошло одновременно с событием х), различия и некоторые другие.

Отношение симметричности символически записывается:

XRy — yRx.

2. Отношение называется рефлексивным (от латинского reflexio — «отражение»), если каждый член отношения находится в таком же отношении к самому себе. Таковы отношения равенства (если а = Ь, тоа = аиЬ = Ь)и одновременности (если событие х произошло одновременно с событием у, значит, каждое из них произошло одновременно с самим собой).

Отношение рефлексивности записывается:

xRy -+ xRx Л yRy.

3. Отношение называется транзитивным (от латинского transitivus — «переход»), если оно имеет место между х и z тогда, когда оно имеет место между х и у и между у и z. Иначе говоря, отношение является транзитивным (переходным) тогда и только тогда, когда из отношения между х и у и между у и z следует такое же отношение между х и z.

Транзитивными являются отношения равенства (если а равно b и b равно с, то а равно с), одновременности (если событие х произошло одновременно с событием у и событие у одновременно с событием z, значит, событие х произошло одновременно с событием z), отноше­ния «больше», «меньше» (а меньше b, b меньше с, значит, а меньше с), «позднее», «находиться севернее (южнее, восточнее, западнее)», «быть ниже, выше» и т. п.

Отношение транзитивности записывается:

(xRy Л yRz) -* xRz.

Для получения достоверных заключений из суждений с отношени­ями необходимо опираться на правила:

Для свойства симметричности (xRy