
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложные суждения: логическая структура и видыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сложные суждения – это суждения, образованные их простых посредством той или иной логической связи. Структура сложных суждений отличается от структуры простых суждений. Основными структурообразующими элементами здесь выступают не понятия (термины – субъект и предикат), а самостоятельные простые суждения, внутренняя субъектно-предикатная структура которых уже не учитывается. Связь между элементами сложного суждения осуществляется с помощью логических союзов: «и», «или»; «если...то...»; «если и только если..., то»; «неверно, что...», которые близки к соответствующим грамматическим союзам, но полностью с ними не совпадают. Главное их отличие состоит в том, что логические союзы однозначны, тогда как грамматические союзы имеют множество смыслов и оттенков. Эти типы связи простых суждений выражаются соответствующими логическими связками: конъюнкцией («и»), дизъюнкцией («или»), строгой дизъюнкцией («либо,...либо»), импликацией («если..., то»), эквиваленцией (тогда и только тогда, когда...», отрицанием («неверно, что...»). Логические связки обозначают символами: Сложные суждения рассматриваются в логике только с точки зрения их истинностных значений, которые зависят от истинностных значений простых суждений, входящих в него, а также от характера связи этих суждений. Характер связи определяется смыслом логических союзов, который состоит в ответе на вопрос: при каких условиях сложное суждение будет истинно, а при каких – ложно. Иначе говоря, при каких сочетаниях истинности и ложности простых суждений, входящих в сложное, данный логический союз дает истинную связь, а при каких - ложную. Смысл логических союзов можно определить с помощью, так называемой истинностной таблицы, в которой на входе (см. Табл.1, столбцы 1,2) выписываются все возможные комбинации истинностных значений простых суждений (входящих в рассматриваемое сложное), а на выходе (Таблица 1 – столбцы 3 – 9) – значения сложного суждения, образованного из данных простых с помощью соответствующего логического союза. При этом, исходные простые суждения обозначают буквами: А,В,С,D..., а значения истинности символами: «и» - истино; «л» - ложно. Таблица 1.
Виды сложных суждений По характеру логической связи выделяют пять основных видов сложных суждений: соединительные (конъюнктивные), разделительные (дизъюнктивные), условные (импликативные), эквивалентные, отрицаемые. Соединительное или конъюнктивное суждение – это сложное суждение, образованное из исходных суждений посредством логического союза «и», обозначаемого символом « Конъюнктивное суждение истинно только при истинности всех составляющих его элементов и ложно при ложности хотя бы одного из них (см. табл.1 – столбец 3). Знание особенностей истинностного значения конъюнкции имеет особое значение в практике мышления, т.к. достаточно одного ложного суждения, чтобы придать всей, даже весьма сложной, конъюнктивной мысли ложность. Этот факт лежит в основе многих русских пословиц, например, о том, что делает ложка дегтя в бочке меда. Эту особенность важно учитывать в юридической практике, в дискуссиях – когда выстраивается сложная цепь мыслей, которая при одном ложном звене может распасться. С другой стороны, достаточно обнаружить хотя бы один ложный аргумент в доводах оппонента, чтобы опровергнуть все его рассуждение в целом. Разделительное или дизъюнктивное суждение – это сложное суждение, образованное из исходных суждений посредством логического союза «или», обозначаемого символом « Поскольку связка «или» употребляется в двух разных значениях – неисключающем и исключающем, то различают слабую и сильную дизъюнкции соответственно. Выше приведенный пример является слабой дизъюнкцией, т.к. право одновременно в одном отношении может способствовать развитию экономики, но препятствовать в другом. Слабая дизъюнкция является истинной в тех случаях, когда истинно по крайней мере одно из составляющих ее суждений (или оба вместе) и ложна, когда оба составляющих ее суждения ложны (Табл.1 – столбец 4). Сильная дизъюнкция (символ « Среди дизъюнктивных суждений следует различать также полную и неполную дизъюнкцию, когда соответственно: перечислены все признаки, виды определенного рода или это перечисление остается открытым (неполным), что в естественном языке выражается словами: «и т.д.», «и др.». Дизъюнктивные суждения широко распространены в практике мышления. Именно в них выражается логическая операция деления. Условное или импликативное суждение – это сложное суждение, в котором суждения объединяются логическим союзом «если..., то» (символ « Образуя условное суждение, прежде всего, имеют в виду, что не может быть так, чтобы то, о чем говорится в основании имело место, а то, о чем говорится в следствии отсутствовало. Иными словами, не может случится, чтобы антецедент был истинным, а консеквент – ложным. Это и определяет то, что условное суждение истинно во всех случаях, кроме одного: когда предшествующее есть, а последующего нет (т.е. – суждение по форме А В форме условных суждений выражают как объективные зависимости одних объектов от других, так и права и обязанности людей, связанные с теми или иными условиями. Эквивалентное суждение – это сложное суждение, в котором объединяются суждения с взаимной условной зависимостью. Поэтому они также называются двойной импликацией. Они образуются с помощью логического союза «если и только если..., то», который обозначается символом « Условия истинности эквивалентных суждений представлены в 7-ом столбце таблицы 1: эквивалентное суждение истинно в двух случаях – когда оба составляющих его суждения истинны или когда оба ложны. Иными словами, связь (отношение) между элементами эквивалентного суждения можно охарактеризовать как необходимую: истинность А достаточна для признания истинности В и наоборот; ложность А служит показателем ложности В и наоборот. Отрицаемое суждение – это сложное суждение, образованное с помощью логического союза «неверно, что...» (или просто «не»), который именуется знаком отрицания (символ «~»). В отличие от вышеотмеченных бинарных союзов он относится к одному суждению. Прибавление его к какому-либо суждению означает образование нового суждения, которое находится в определенной зависимости от исходного: отрицаемое суждение истинно, если исходное ложно, и наоборот. Это выражено в таблице1 – столбцы 8,9. Например, если исходное суждение: «Все свидетели правдивы», то отрицаемое: «Неверно, что все свидетели правдивы». Все выделенные виды сложных суждений используются в обычных рассуждениях и контекстах, в том числе экономических и правовых. Для более точного уяснения смысла этих контекстов важно овладение навыками логического анализа сложных суждений с использованием символического языка для выражения их логической структуры. Часто для достижения определенности высказывания необходимо выявить главную связь в суждении. Например, высказывание «Преступление совершено А и В или С» не отличается определенностью, поскольку не ясно, какая из двух логических связок – конъюнкция или дизъюнкция – является главной. Поэтому данное высказывание может быть истолковано как конъюнктивное суждение (1): «А и (В или С)», а может и как дизъюнктивное суждение (2): «(А и В) или С». Но по логической значимости, т.е. по их истинностному значению, они не эквиваленты. Это можно определить, построив для них истинностные таблицы, и по ним сравнить истинностные значения этих суждений. С этой целью важно знать, как вообще строятся истинностные таблицы для различных сложных суждений. Осуществляется это следующим образом. На входе таблицы: 1. Выписывают все простые суждения (А, В, С, D...), входящие в рассматриваемое сложное суждение. Пусть их число будет n. 2. Определяют число к строк в таблице по формуле к = 2n 3. В столбцах входа таблицы выписывают все возможные комбинации истинностных значений простых суждений в следующем порядке: в самом правом столбце чередуют и и л по одному; во втором справа столбце чередуют подряд два значения и и два значения л; в третьем столбце чередуют подряд четыре значения и и четыре значения л; в четвертом столбце – восемь значений и подряд и восемь значений л подряд и т.д. На выходе таблицы: 4. Слева направо выписывают логические формы всех сложных суждений, входящих в рассматриваемое суждение, по порядку: в начале суждения 1-ой степени сложности (т.е. с одним логическим знаком); затем 2-ой степени (с двумя логическими союзами); далее 3-ей степени (с тремя логическими союзами) и так до тех пор, пока последнее суждение не будет представлять логическую форму исходного сложного суждения. 5. Столбцы истинностных значений для выписанных логических форм образуют исходя из: (1) смысла логического союза (см. таблицу 1) и (2) значений истинности, которые принимают простые суждения, входящие в данную форму (см. строки входа таблицы). Мы можем сравнить вышеотмеченные суждения (1) и (2). С этой целью теперь построим таблицу 2 для конъюнктивного суждения (1), выразив его символически как «А
Из таблиц 2 и 3 видно, что истинностные значения суждений (1) и (2) не одинаковы (в двух строках – когда одно ложно, другое истинно), и следовательно они не эквивалентны, и представляют суждения, выражающие различные связи между их структурными элементами. Таким образом, для осуществления логического анализа формы сложных суждений необходимо записать их символически в виде формулы и построить соответствующие истинностные таблицы с последующим их сравнением. Отношения между суждениями Между суждениями существуют логические отношения. Суждения как и понятия, могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми. Но есть существенные различия, вызванные их различной логической структурой. Если сравнимые понятия соотносятся друг с другом по их объему, то между сравнимыми суждениями имеются многообразные отношения прежде всего по их истинностным значениям. Анализ этих отношений предполагает выяснение таких вопросов: могут ли рассматриваемые суждения быть вместе истинными, вместе ложными, обусловливает ли истинность одного истинность другого и ложность одного ложность другого. Такой анализ имеет важное теоретическое и практическое значение, но его осуществление имеет свою специфику относительно простых и сложных суждений, поскольку они различаются своей логической структурой. Отношения суждений по их истинностным значениям исследуются в логике между сравнимыми суждениями. Несравнимые простые суждения имеют разные субъекты и предикаты, например: «Закон суров» и «Небо ясное». Истинность и ложность таких суждений не зависит друг от друга. Сравнимые простые суждения имеют одинаковые субъект и предикат (поэтому они и сравнимы по содержанию), но различаются количественными и качественными характеристиками логической формы. Несравнимые сложные суждения включают в себя полностью или частично разные по содержанию простые суждения. Например, суждения: «Прокуроры и следователи имеют юридическое образование» и «Прокуроры и следователи стоят на страже законности». Сравнимые сложные суждения включают одинаковые исходные простые суждения, а различаются типом связи между ними (т.е. логическими союзами). Например: «Кража и мошенничество строго караются по закону», «Кража или мошенничество строго караются по закону», «Неверно, что кража и мошенничество строго караются по закону». Между сравнимыми суждениями выделяются два типа отношений: совместимость и несовместимость. Суждения рассматриваются как совместимые, если они могут быть одновременно истинными, и как несовместимые, если они не могут быть одновременно истинными. Совместимость бывает трех видов: эквивалентность, подчинение и частичная совместимость. 1. Суждения эквивалентны, если они всегда принимают одинаковые истинностные значения. Простые категорические суждения (А, Е, J, О) находятся в отношении эквивалентности, если они различны по количеству и качеству, и одно из них стоит под отрицанием: ~ А эквивалентно О («Неверно, что все юристы адвокаты» эквивалентно «Некоторые юристы не адвокаты»); ~ О эквивалентно А («Неверно, что некоторые адвокаты не юристы» эквивалентно «Все адвокаты юристы»); ~ J эквивалентно Е («Неверно, что некоторые студенты профессора» эквивалентно «Ни один студент не профессор»); ~ Е эквивалентно J («неверно, что ни один гриб не ядовит» эквивалентно «Некоторые грибы ядовиты»). Сложные суждения находятся в отношении эквивалентности, когда при одних и тех же значениях истинности исходных простых суждений они принимают одинаковые значения. Это всегда можно установить построением истинностных таблиц для рассматриваемых сложных суждений. 2. Суждение находится в отношении подчинения к другому (подчиняющему), если оно истинно во всех тех случаях, когда истинно подчиняющее. Это отношение имеет место между простыми категорическим суждениями, у которых количество различно, а качество одно и то же. В таком отношении находятся: общеутвердительные (А) и частноутвердительные (J) суждения; общеотрицательные (Е) и частноотрицательные (О) суждения. Здесь действуют такие закономерности: (1) из истинности общего (А или Е) следует соответственно истинность частного (J или О), но не наоборот; (2) из ложности частного (J или О) следует ложность общего (А или Е), но не наоборот. Например, если истинно «Все студенты нашей группы - успевающие» (А), то тем более истинно «Некоторые студенты нашей группы успевающие» (J). В свою очередь, если ложно «Некоторые люди вправе нарушать закон» (J), то тем более ложно, что «Все люди вправе нарушать закон» (А). Отношение подчинения в сложных суждениях имеет свойства логического следования, которое характеризуется тем, что при истинности подчиняющего суждения В подчиненное суждение С всегда истинно, и не может быть так, что суждение В истинно, а суждение С – ложно. Например: «Если у человека повышенная температура (В), то он болен (С)». При наличии температуры у человека (В) – истинно, следует с необходимостью истинность суждения (С). Но при ложности В, суждение С может быть как истинным, так и ложным. 3. Отношение частичной совместимости также имеет место как между простыми, так и сложными суждениями. Для этого отношения характерна следующая закономерность: невозможна совместная ложность суждений, находящихся в отношении частичной совместимости. В случае простых суждений – это отношение между суждениями одинакового количества, но разного качества: между частноутвердительными (J) и частноотрицательными (О) суждениями. Из ложности одного из них следует истинность другого, но не наоборот: из истинности одного из них не следует с необходимостью ложность другого – оно также может быть истинным. Эту закономерность особо следует учитывать в практике мышления. Так, при истинности (J) – «Некоторые следователи независимы» может быть истинным и (О) – «Некоторые следователи не являются независимыми». Но при ложности суждения (J) – «Некоторые следователи независимы» необходимо будет истинным противоположное по качеству суждение, т.е. (О) – «Некоторые следователи не являются независимыми». Рассмотрим теперь несовместимые суждения. Различают два вида несовместимости: противоречие и противоположность. Противоречие – это такое отношение между суждениями, при котором истинность одного необходимо влечет ложность другого и наоборот. Иными словами, противоречивые суждения не могут вместе быть ни истинными, ни ложными. Среди простых суждений это отношение имеет место между: общеутвердительными (А) и частноотрицательными (О) суждениями; общеотрицательными (Е) и частноутвердительными (J) суждениями. Так, если ложно суждение «Все следователи независимы», то истинно «Некоторые следователи не являются независимыми». Отношение противоречия между сложными суждениями означает, что их истинностные значения могут лишь исключать друг друга. Противоположность между суждениями проявляется в том, что данные суждения не могут быть вместе истинными, но могут быть вместе ложными. Для этого отношения характерна закономерность обратная той, которая характерна для отношения частичной совместимости: если одно из двух суждений истинно, то другое необходимо ложно, но при ложности одного из них другое может быть как истинным, так и ложным. Иными словами, возможна ложность обоих суждений. В случае простых суждений, это отношение имеет место между общеутвердительными (А) и общеотрицательными (Е) суждениями. Так, если истинно (А) – «Все адвокаты – юристы», то ложно (Е) – «Ни один адвокат не юрист». Но если ложно (А) – «Все свидетели правдивы», то из него не следует истинность суждения (Е) – «Ни один свидетель не правдив», оно тоже ложно. Но в других случаях (Е) может быть истинным. Так, если ложно суждение (А) – «Все граждане вправе нарушать закон», то истинно (Е) – «Ни один гражданин не вправе нарушать закон». Знание отношений между суждениями по их истинным значениям важно в познавательном и практическом планах, поскольку помогает избегать возможных ошибок в собственных рассуждениях, позволяет грамотно анализировать различные контексты, высказывания оппонентов. Часто встречаются ситуации, когда суждениями оперируют как исключающими друг друга. Например, когда кто-то выдвигает суждение в форме «Некоторые S есть Р», а другой - в форме «Некоторые S не есть Р». Логический же анализ этих суждений показывает, суждения, высказанные в такой форме, не исключают друг друга, а являются частично совместимыми, и оба могут оказаться истинными. Весьма часто также в споре из истинности частного суждения (J или О) выводят истинность общего (А или Е) соответственно, что нарушает правильность отношений между ними. В дискуссии, споре, в частности по юридическим и экономическим вопросам, чтобы опровергнуть общее ложное суждение, часто используют противоположное ему общее суждение. Но так легко попасть впросак: оно тоже может оказаться ложным. В логическом отношении для точного опровержения достаточно привести противоречащее суждение (см. ниже схему логического квадрата). Смешение противоположных и противоречащих суждений довольно частая ошибка в практике мышления. Поэтому важно уметь осуществлять логический анализ отношений между суждениями. Для осуществления логического анализа отношений между простыми суждениями используют графическую схему, называемую «логическим квадратом»: его вершины символизируют четыре вида простых категорических суждений – А, Е, J, О; стороны и диагонали – отношения между этими суждениями.
Чтобы определить отношение между простыми категорическими суждениями, нужно: 1. определить, какого вида эти суждения: А, Е, J, О; 2. найти соответствующие углы логического квадрата; 3. посмотреть какое отношение вписано между ними; 4. по характеру отношения установить связь истинностных значений для анализируемых суждений. Например, нужно определить отношение между суждениями: (1) «Не все металлы твердые» и (2) «Некоторые металлы твердые». Для этого осуществим их логический анализ. Прежде всего, определяем вид суждений (1) и (2): второе суждение – частноутвердительное (J), а первое суждение – общеутвердительное с отрицанием. Превращаем его согласно приведенным выше эквивалентностям (~ А эквивалентно О) в эквивалентное суждение – О. Определяем по логическому квадрату отношение между J и О. Отношение между ними – частичная совместимость, что означает, что совместная ложность невозможна, но возможна совместная истинность. Для определения отношений между сложными суждениями нужно: 1. определить по главному логическому союзу вид анализируемых сложных суждений; 2. записать символически в виде формул их логические формы; 3. построить их совместную истинностную таблицу; 4. сравнить истинностные значения формул данных суждений и по их характеру определить вид отношения. В качестве примера определим отношения между суждениями: (1) «Он не читает ни детективных, ни исторических романов» и (2) «Он читает либо детективные, либо исторические романы». Первое суждение – конъюнктивное, состоит из двух отрицательных суждений: «Он не читает детективных романов» (~ А), «Он не читает исторических романов» (~ В), соединительный союз (
Сравнивая результирующие столбцы (два крайних справа), которые представляют формулы суждений (1) и (2), видим, что эти суждения не бывают одновременно истинными, значит они несовместимые суждения. Но в первой строке обнаруживаем их совместную ложность, следовательно они находятся в отношении противоположности.
|

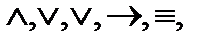 ~ соответственно. Каждый из этих логических союзов, за исключением отрицания, является бинарным, т.е. соединяет только два суждения, независимо от того простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы.
~ соответственно. Каждый из этих логических союзов, за исключением отрицания, является бинарным, т.е. соединяет только два суждения, независимо от того простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы. В
В
 В
В
 В
В
 В
В
 В
В
 ». Например, суждение: «Сегодня я пойду на лекцию по логике и в кино» является конъюнктивным суждением, состоящим из двух простых суждений (обозначим их соответственно – А, В):: «Сегодня я пойду на лекцию по логике» (А), «Сегодня я пойду в кино» (В). Символически данное сложное суждение можно записать как: А
». Например, суждение: «Сегодня я пойду на лекцию по логике и в кино» является конъюнктивным суждением, состоящим из двух простых суждений (обозначим их соответственно – А, В):: «Сегодня я пойду на лекцию по логике» (А), «Сегодня я пойду в кино» (В). Символически данное сложное суждение можно записать как: А  В, где А, В – элементы конъюнкции; «
В, где А, В – элементы конъюнкции; « » - символ логического союза – конъюнкции. В русском языке конъюнктивный логический союз выражается многими грамматическими союзами: и, а, но, да, хотя, однако, а также... Нередко подобные грамматические союзы заменяются запятой, двоеточием, точкой с запятой. Например, в суждении «Русские долго запрягают, да быстро ездят».
» - символ логического союза – конъюнкции. В русском языке конъюнктивный логический союз выражается многими грамматическими союзами: и, а, но, да, хотя, однако, а также... Нередко подобные грамматические союзы заменяются запятой, двоеточием, точкой с запятой. Например, в суждении «Русские долго запрягают, да быстро ездят». ». Например, суждение: «Право может способствовать экономическому развитию или препятствовать ему» является дизъюнктивным суждением, состоящим из двух простых: «Право может способствовать экономическому развитию», «Право может препятствовать экономическому развитию». Соответственно обозначив их через буквы А, В – выделим его логическую форму: А
». Например, суждение: «Право может способствовать экономическому развитию или препятствовать ему» является дизъюнктивным суждением, состоящим из двух простых: «Право может способствовать экономическому развитию», «Право может препятствовать экономическому развитию». Соответственно обозначив их через буквы А, В – выделим его логическую форму: А  В.
В. ») отличается от слабой тем, что ее составляющие исключают друг друга. Например: «Преступление может быть умышленным или по неосторожности». Для того, чтобы подчеркнуть строго разделительный, исключающий характер связи, в естественном языке используется усиленная двойная форма разделения: «...либо...либо», «или...или», например: «Либо я найду путь, либо я проложу его». Строгая дизъюнкция истинна лишь тогда, когда одно из составляющих ее суждений истинно, а другое – ложно (Табл. 1 – столбец 5).
») отличается от слабой тем, что ее составляющие исключают друг друга. Например: «Преступление может быть умышленным или по неосторожности». Для того, чтобы подчеркнуть строго разделительный, исключающий характер связи, в естественном языке используется усиленная двойная форма разделения: «...либо...либо», «или...или», например: «Либо я найду путь, либо я проложу его». Строгая дизъюнкция истинна лишь тогда, когда одно из составляющих ее суждений истинно, а другое – ложно (Табл. 1 – столбец 5). »), например: «Если правительство нарушает закон, то порождает неуважение к нему», «Если число делится на 2 без остатка, то оно четное». Условное суждение состоит из двух составляющих его суждений. Суждение, выраженное после слова «если» называется основанием или антецедентом (предыдущим), а суждение – после слова «то» называется следствием или консеквентом (последующим). Формула условного суждения: А
»), например: «Если правительство нарушает закон, то порождает неуважение к нему», «Если число делится на 2 без остатка, то оно четное». Условное суждение состоит из двух составляющих его суждений. Суждение, выраженное после слова «если» называется основанием или антецедентом (предыдущим), а суждение – после слова «то» называется следствием или консеквентом (последующим). Формула условного суждения: А  В, где А – основание, В – следствие. При этом, суждения, выполняющие роль основания и следствия, сами по себе могут быть как простыми, так и сложными суждениями.
В, где А – основание, В – следствие. При этом, суждения, выполняющие роль основания и следствия, сами по себе могут быть как простыми, так и сложными суждениями. В – ложно только в одном случае, когда А – истинно, а В – ложно). Это выражено в таблице 1 – столбец 6.
В – ложно только в одном случае, когда А – истинно, а В – ложно). Это выражено в таблице 1 – столбец 6. ». Формула эквивалентности: А
». Формула эквивалентности: А  В, где А, В – суждения, из которых образуется эквивалентное суждение, например: «Человек имеет право на пенсию по возрасту, если и только если он достиг пенсионного возраста». В естественном языке, в том числе в экономических и юридических текстах, для выражения эквивалентных суждений используются грамматические союзы: «лишь при условии, что..., то», «только тогда, когда..., то», «в том и только в том случае, когда..., тогда».
В, где А, В – суждения, из которых образуется эквивалентное суждение, например: «Человек имеет право на пенсию по возрасту, если и только если он достиг пенсионного возраста». В естественном языке, в том числе в экономических и юридических текстах, для выражения эквивалентных суждений используются грамматические союзы: «лишь при условии, что..., то», «только тогда, когда..., то», «в том и только в том случае, когда..., тогда». (В
(В  С)», и таблицу 3 для дизъюнктивного суждения (2), записав его символически как «(А
С)», и таблицу 3 для дизъюнктивного суждения (2), записав его символически как «(А  В)
В)  С».
С». С
С
 (В
(В  С)
С)
 В
В
 В)
В)  С
С
 В
В
 ) опущен. Символическая запись формы суждения (1): ~ А
) опущен. Символическая запись формы суждения (1): ~ А  ~В. Второе суждение – строго дизъюнктивное, состоит из двух суждений: «Он читает детективные романы» (А), «Он читает исторические романы» (В), которые связаны двойным разделительным союзом «либо...либо» (
~В. Второе суждение – строго дизъюнктивное, состоит из двух суждений: «Он читает детективные романы» (А), «Он читает исторические романы» (В), которые связаны двойным разделительным союзом «либо...либо» ( ). Поэтому символическая запись логической формы суждения (2): А
). Поэтому символическая запись логической формы суждения (2): А  В. Построим для них совместную истинностную таблицу, где А, В - исходные суждения.
В. Построим для них совместную истинностную таблицу, где А, В - исходные суждения. ~В
~В
 В
В



