
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ограничение третьего понятияСодержание книги
Поиск на нашем сайте
Ограничение третьего понятия – это такая форма непосредственного умозаключения, которая позволяет из суждения вида S a P, где a – какая-либо из констант A, E, I, O, выводить суждение вида s S as P, где s – есть некоторое общее или единичное имя, а «s S» и «s P» обозначает новое общее имя «s, обладающая свойством S» и «s, обладающая свойством P» соответственно. Например:
Данная операция применима также к единичным суждениям, например:
Очень важно отличать операцию ограничения третьего понятия от неправильной формы рассуждения, называемой «ограничение третьим понятием». Например: И еще более очевидный пример: Умозаключение по логическому квадрату Учитывая отношения между категорическими суждениями А, Е, I, О, которые изображаются с помощью «логического квадрата», можно строить выводы, основываясь на истинности или ложности исходного суждения. Выводы строятся по следующим правилам: Отношения противоречия (А-О; Е-I):
Отношение проотивоположности или контрарности (А-Е):
Отношение подпротивности или субконтрарности (I-О):
Отношение подчинения (А-I; Е-О):
В качестве примера можно построить вывод на отношения противоположности (A-E), из общеутвердительного суждения (A): «Все жидкости упруги», – истинность которого установлена, можно сделать заключение о ложности общеотрицательного суждения (E): «Неверно, что ни одна жидкость не является упругой». 30) Сокращённые силлогизмы. Перейдём к рассмотрению тех силлогизмов, которые называются сокращёнными и сложными силлогизмами; они по форме отличаются от обыкновенных. Некоторые утверждали, что мы в мышлении никогда не пользуемся силлогизмами. Но это неправильно, потому что в обиходной жизни мы пользуемся весьма часто силлогизмом, но только он не всегда бывает выражен полно, и именно оттого, что некоторые части его бывают выпущены. Эти силлогизмы называются сокращёнными, или также энтимемами. Это название происходит от греческого слова enthymema. Энтимема – это такой силлогизм, часть которого мы держим в уме (???????), а часть выражаем. Мы можем выбрасывать каждую часть силлогизма и мыслить всё-таки силлогистически. Например, если мы относительно кого-нибудь употребим выражение: «нужно быть дурным человеком, чтобы делать подобные вещи», то это выражение представляет собой силлогизм, который, если мы ему придадим полную форму, приобретёт следующий вид:
Все люди, которые делают подобные вещи, дурны. Этот человек делает подобные вещи. Следовательно, он дурной человек Для того чтобы пояснить, как происходит этот пропуск частей силлогизма, возьмём какой-нибудь полный силлогизм, например: Всякий порок заслуживает порицания. Скупость есть порок. Следовательно, скупость заслуживает порицания. Этим примером можно воспользоваться для того, чтобы иллюстрировать следующие три вида энтимемы. Вид 1: Скупость заслуживает порицания, потому что она есть порок. (Здесь пропущена большая посылка.) Вид 2: Скупость заслуживает порицания, потому что всякий порок заслуживает порицания. (Здесь пропущена меньшая посылка.) Вид 3: Всякий порок заслуживает порицания, скупость же есть порок… (Здесь пропущено заключение и именно потому, что оно очевидно.) Эпихейрема. Есть, наконец, ещё один вид сокращённых силлогизмов, который называется эпихейремой. Это такой силлогизм, в обе посылки которого входят энтимемы. Схема эпихейремы: M есть P, так как оно есть N. S есть M, так как оно есть O. Следовательно, S есть P. Первая посылка должна была бы быть выражена так: Все N суть P. Все M суть N. Следовательно, M есть P. Вторая посылка должна была бы быть выражена так: Все O суть M. Все S суть O. Следовательно, все S суть M. Пример: Ложь заслуживает презрения, так как она безнравственна. Лесть есть ложь, так как она есть умышленное извращение истины. Следовательно, лесть должна быть презираема. В этом силлогизме, как это легко видеть, каждая из посылок есть суждение, которое представляет собой заключение со средним термином; если же дать заключение со средним термином, то этого вполне достаточно, для того чтобы восстановить весь силлогизм. Теперь рассмотрим те силлогизмы, которые называются сложными. Полисиллогизмы. Может случиться, и собственно в научной мысли весьма часто бывает, что мы несколько силлогизмов соединяем в один, и тогда получается то, что называется цепью силлогизмов – полисиллогизм. Соединение силлогизмов происходит таким образом, что заключение одного силлогизма является посылкой для другого; тот силлогизм, который предшествует, называется просиллогизмом; тот силлогизм, который следует после, называется эписиллогизмом.
Схема полисиллогизма будет следующая: Просиллогизм: Все B суть A Все C суть B Следовательно, все C суть A Эписиллогизм: Все C суть A Все D суть C Следовательно, все D суть A Есть два типа полисиллогизмов. В первом умозаключение идёт от более общего к менее общему, во втором, наоборот, умозаключение идёт от менее общего к более общему. Первый тип называется прогрессивным, второй – регрессивным. Пример прогрессивного полисиллогизма: Все позвоночные имеют красную кровь. Все млекопитающие суть позвоночные. Все млекопитающие имеют красную кровь. Все млекопитающие имеют красную кровь. Все хищные суть млекопитающие. Все хищные имеют красную кровь. Все хищные имеют красную кровь. Тигры суть хищные животные. Тигры имеют красную кровь. Здесь умозаключение идёт от более общего к менее общему (позвоночные, млекопитающие, хищные, тигры), т.е. шествует вперёд по отношению к содержанию, так как в частных понятиях содержание больше. Пример регрессивного полисиллогизма: Позвоночные суть животные. Тигры суть позвоночные. Тигры суть животные. Животные суть организмы. Тигры суть животные. Тигры суть организмы. Организмы разрушаются. Тигры суть организмы. Тигры разрушаются. Здесь умозаключение идёт от менее общего к более общему (позвоночное, животное, организм, разрушимое). Сориты. Иногда при соединении нескольких силлогизмов для плавности мысли мы можем пропускать некоторые посылки. В таком случае получается то, что называется соритом (от греч.????? – куча). Существует два вида соритов: 1) аристотелевский, когда выбрасывается меньшая посылка каждого отдельного силлогизма, и 2) гоклениевский, когда выбрасывается большая посылка отдельных силлогизмов. Возьмём примеры: 1. Аристотелевский сорит. Буцефал есть лошадь. Лошадь есть четвероногое. Четвероногое есть животное. Животное есть субстанция. Буцефал есть субстанция. Если бы этому сориту мы придали полную форму, т.е. восстановили бы опущенные посылки, то у нас получилось бы следующих три силлогизма: 1) Лошадь есть четвероногое. Буцефал есть лошадь. Буцефал есть четвероногое 2) Четвероногое есть животное. (Буцефал есть четвероногое). Буцефал есть животное. 3) Животное есть субстанция. (Буцефал есть животное). Буцефал есть субстанция 2. Гоклениевский сорит. Животное есть субстанция. Четвероногое есть животное. Лошадь есть четвероногое. Буцефал есть лошадь. Буцефал есть субстанция. Это есть гоклениевский сорит, потому что выпущены большие посылки. Если бы мы восстановили пропущенные посылки, то у нас получился бы следующий ряд силлогизмов: 1) Животное есть субстанция. Четвероногое есть животное. Четвероногое есть субстанция. 2) [Четвероногое есть субстанция]. Лошадь есть четвероногое. Лошадь есть субстанция. 3) [Лошадь есть субстанция]. Буцефал есть лошадь. Буцефал есть субстанция. 31) Формальная логика - наука о законах и формах правильного мышления. В. С. Меськов пишет: “...Предметом науки логики являются рассуждения, а сама она есть наука о рассуждениях. Задачей логики как науки является установление законов и правил, которым подчиняются рассуждения”'. Рассуждения облекаются в логическую форму и строятся в соответствии с логическими законами. “...Логические формы и законы не пустая оболочка, а отражение объективного мира”2. Выясним более детально, что понимается под логической формой и логическим законом.
Понятие логической формы Логической формой конкретной мысли является строение этой мысли, т.е. способ связи ее составных частей. Логическая форма отражает объективный мир, но это отражение не всей полноты содержания мира, существующего вне нас, а его общих структурных связей, которые необходимо воплощаются и в структуре наших мыслей. Понятия, суждения, умозаключения имеют свои специфические формы (структуры). Структура мысли, т.е. ее логическую форму, можно выразить при помощи символов. Выявим структуру (логическую форму) трех следующих суждений: “Все караси - рыбы”, “Все люди смертны”, “Все бабочки - насекомые”. Содержание у них разное, а форма одна и та же: “Все S суть Р”; она включает S (субъект), т. е. понятие о предмете суждения, Р (предикат), т. е. понятие о признаке предмета, связку (“есть”, “суть”), кванторное слово (“все”). Иногда связка может отсутствовать или заменяться на тире. Два следующих условных суждения имеют одну и ту же форму: 1) “Если железо нагревать, то оно расширяется”; 2) “Если учащийся изучает логику, то он повышает четкость своего мышления”. Форма этих суждений такая: “Если S есть Р, то S есть Р1”. Логические законы Соблюдение законов логики - необходимое условие достижения истины в процессе рассуждения. Основными формально-логическими законами обычно считаются: 1) закон тождества; 2) закон непротиворечия, 3) закон исключенного третьего; 4) закон достаточного основания. Они будут подробно излагаться в отдельной главе. Эти законы (принципы) выражают определенность, непротиворечивость, доказательность мышления. Логические принципы действуют независимо от воли людей, они не созданы по их воле и желанию, а являются отражением связей и отношений вещей материального мира. Общечеловеческийхарактер принципов формальной логики состоит в том, что во все исторические эпохи все люди мыслили по одним и тем же логическим принципам. Кроме формально-логических принципов, правильное мышление подчиняется также основным законам диалектики: закону единства и борьбы противоположностей, закону взаимного перехода количественных и качественных изменений, закону отрицания отрицания.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.175.114 (0.012 с.) |




 .
.
 (
( ;
;  ).
). (
( );
);  .
. (
(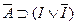 ;
;  ;
;  ;
;  )
)


