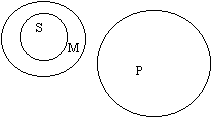Истинность мысли и формальная правильность рассуждений

Понятие истинности (ложности) относится лишь к конкрет­ному содержанию того или иного суждения. Если в суждении верно отражено то, что имеет место в действительности, то оно истинно, в противном случае оно ложно. Например, суждение “Все волки - хищные животные” истинно, а суждение “Все гри­бы - ядовиты” ложно.

Понятие формальной правильности рассуждения относится лишь к логическим действиям и операциям мышления. Если в числе посылок умозаключения встречается ложная посылка, то при соблюдении правил логики мы в заключении можем полу­чить и истину, и ложь. Чтобы это показать, возьмем два умоза­ключения:

1. Все металлы - твердые тела.

Ртуть не является твердым телом.

Ртуть не является металлом.

1. Все небесные тела – планеты

Юпитер-небесное тело.

Юпитер - планета.

В первом умозаключении заключение получилось ложным именно потому, что в качестве первой посылки взято ложное суждение. Во втором же умозаключении, несмотря на первую ложную посылку, заключение является истинным суждением.

Чтобы заключение было истинным, обе посылки должны быть истинными суждениями и соблюдаться правила логики. При не­соблюдении правил логики (если посылки при этом истинны) мы также можем получить как истинное, так и ложное заключение. Чтобы это показать, возьмем такие умозаключения:

1. Все тигры полосатые.

Это животное полосатое.

Это животное - тигр

4. Все ушастые тюлени – ластоногие.

Все ушастые тюлени - водные млекопитающие

_____________________________________

Все водные млекопитающие -ластоногие.

 

В третьем умозаключении обе посылки - истинные сужде­ния, но полученное заключение может быть как ложным, так и истинным потому, что нарушено было одно из правил умозаклю­чения. В четвертом умозаключении обе посылки - истинные суждения, но заключение - ложное, т. к. нарушено правило по­строения умозаключения (в соответствии с правилом, вместо слова “все” должно стоять слово “некоторые”).

Итак, с точки зрения содержания мышление может давать истинное или ложное отражение мира, а со стороны формы оно может быть логически правильным или неправильным. Истинность есть соответствие мысли действительности, а правиль­ность мышления - соблюдение законов и правил логики. Нель­зя отождествлять (смешивать) следующие понятия: “истин­ность” (“истина”) и “правильность”, а также понятия “ложность” (“ложь”) и “неправильность”.

Современная логика - это интенсивно развивающаяся наука, которая включает в себя логику формальную и логику диалекти­ческую. На их базе формируется логика научного познания, использующая методы обеих наук для анализа научного знания.

Как уже отмечалось, формальная логика - наука о законах и формах правильного мышления. Формальная логика в определен­ном смысле подобна грамматике. К. Д. Ушинский считал логику грамматикой мышления. Подобно грамматике, придающей языку стройный и четко осмысленный характер, логика обеспе­чивает доказательность и стройность мышления.

32) Категорический силлогизм – вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, связанных средним термином, при соблюдении правил вывода необходимо следует заключение.

Понятия, входящие в состав силлогизма, называются терминами силлогизма. В простом категорическом силлогизме только 3 термина:

больший термин (Р) – предикат заключения;

меньший термин (S) – субъект заключения;

средний термин (М) – связывает в посылках Р и S, в заключении отсутствует.

Структуру простого категорического силлогизма составляют две посылки и заключение. Посылка, содержащая больший термин (Р), называется большей посылкой; посылка, содержащая меньший термин (S) – меньшей посылкой.

Все жидкости (М) – упруги (Р) – большая посылка

Ртуть (S) – жидкость (М) – меньшая посылка

Ртуть (S) – упруга (Р) – заключение

33) Общие правила простого категорического силлогизма

Правила терминов

1. В силлогизме должно быть только три термина (S, P, M). Нарушение этого правила ведёт к ошибке "учетверение терминов":

Движение (М) – вечно (Р)

Хождение в школу (S) – движение (М)

Хождение в школу вечно

В данном силлогизме средний термин "движение" употребляется в разных смыслах – в предельно широком (философском) и обыденном (движение как перемещение). Заключение ложно.

2. Средний термин должен быть распределён по крайней мере в одной из посылок.

Все гусеницы (Р) едят салат (М)

Я (S) ем салат (М)

Я – гусеница

Средний термин (те, кто едят салат) не распределён ни в одной из посылок. Вывод ложный.

3. Термин в заключении может быть распределён только тогда, когда он распределён в посылке.

Во всех городах за полярным кругом (М) – белые ночи (Р)

Санкт-Петербург (S) – не за полярным кругом (М)

В Санкт-Петербурге не бывает белых ночей.

Предикат вывода распределён в заключении, но не распределён в посылке. В терминах заключения говорится больше, чем в посылках: произошло расширение большего термина. Заключение ложно.

Правила посылок

1. Из двух отрицательных посылок вывод не производится.

Дельфины не рыбы.

Щуки не дельфины.

?

2. Если одна из посылок отрицательная, то и заключение должно быть отрицательным:

Некоторые люди не умеют читать.

Все люди умеют смеяться.

Некоторые из умеющих смеяться не умеют читать.

3. Из двух частных посылок нельзя сделать вывод:

Некоторые животные живут в воде.

Некоторые говорящие существа – животные.

?

4. Если одна из посылок частная, то заключение должно быть частным:

Все люди обладают сознанием.

Некоторые двуногие существа – люди.

Некоторые двуногие существа обладают сознанием.

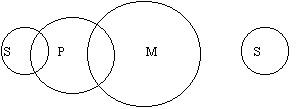
Анализ простых категорических силлогизмов с помощью круговых схем

Правильность силлогизма можно легко проверить без знания фигур, модусов и даже общих правил простого категорического силлогизма, опираясь только на иллюстрацию отношения понятий кругами Эйлера. Это называется методом круговых схем для отбора правильных силлогизмов.

Логическим основанием данного метода является следующая закономерность: если силлогизм построен правильно, то на схеме отношений понятий-терминов (Р, М, S) данного силлогизма их взаимное расположение, заданное суждениями-посылками, будет абсолютно однозначно определять отношение объёмов понятий субъекта и предиката заключения.

Все 19 модусов простого категорического силлогизма в конечном счёте сводимы к четырём правильным модусам первой фигуры, дающим четыре возможных вида выводов: общеутвердительный (А), общеотрицательный (Е), частноутвердительный (I) и частноотрицательный (О). Значит, и схем расположения терминов в правильном силлогизме возможно только четыре. Они представлены на следующих рисунках:

Вывод А

Все М есть Р Все S есть М Все S есть Р   Все люди смертны Сократ – человек Сократ смертен

Вывод Е

Ни одно М не есть Р Все S есть М Ни одно S не есть Р   Ни одно дерево не летает Все берёзы – деревья Ни одна берёза не летает

Вывод I

Все М есть Р Некоторые S есть М Некоторые S есть Р   Все зебры – полосатые Некоторые лошади – зебры Некоторые лошади – полосатые

Вывод О

Ни одно М не есть Р Некоторые S есть М Некоторые S не есть Р   Ни одно растение не говорит Некоторые формы жизни – растения Некоторые формы жизни не говорят

Примеры ошибок:

а) Все студенты сдают экзамены, а некоторые водители не сдают экзаменов. Значит, некоторые водители – не студенты. Все Р есть М Некоторые S не есть М Некоторые S не есть Р

б) Некоторые студенты занимаются музыкой, а ни один попугай музыкой не занимается, следовательно некоторые попугаи не являются студентами. Некоторые Р есть М Ни одно S не есть М Некоторые S не есть Р

В обоих примерах вывод с необходимостью не следует из посылок, поскольку отношение субъекта и предиката в заключении не однозначно.

34) Фигуры и модусы простого категорического силлогизма

Фигурами категорического силлогизма называются формы силлогизма, различающиеся по положению среднего термина (М) в посылках. Имеется четыре фигуры категорического силлогизма:

I-ая фигура

Все злаки (М) – растения (Р) Рожь (S) – злак (М) Рожь (S) – растение (P)

II-ая фигура.

Все ужи (Р) – пресмыкающиеся (М) Это животное (S) – не пресмыкающееся (М) Это животное (S) – не уж (Р)

III-я фигура.

Все углероды (М) – простые тела (Р) Все углероды (М) – электропроводники (S) Некоторые электропроводники (S) – простые тела (Р)

IV-ая фигура.

Все киты (Р) – млекопитающие (М) Ни одно млекопитающее (М) – не рыба (S) Ни одна рыба (S) – не кит (Р)

Каждая фигура категорического силлогизма имеет свои особые правила:

I фигура:	Большая посылка – общая, меньшая посылка – утвердительная.
II фигура:	Большая посылка – общая, одна из посылок – отрицательная.
III фигура:	Меньшая посылка – утвердительная, заключение – частное.
IV фигура:	Заключение не может быть общеутвердительным суждением.

В каждой фигуре возможно несколько допустимых (правильных) сочетаний посылок и заключения. Такие сочетания называются модусами.

Модусы фигур категорического силлогизма – разновидности силлогизма, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключений.

Всего в фигурах силлогизма 19 правильных модусов. Каждому модусу присвоено латинское название, в котором гласные буквы последовательно обозначают вид суждений большей посылки, меньшей посылки и заключения.

I фигура:	Barbara, Celarent, Darii, Ferio; ААА, ЕАЕ, АII, ЕIО.
II фигура:	Cezare, Camestres, Festino, Baroko; ЕАЕ, АЕЕ, ЕIО АОО;
III фигура:	Darapti, Disamis, Datisi, Felapton, Вocardo, Ferison; ААI, IАI, АII, ЕАО, ОАО, ЕIО.
IV фигура:	Bramantip, Camenes, Dimaris, Fesapo, Fresison; ААI, АЕЕ, IАI, ЕАО, ЕIО.

Чтобы получить истинное заключение в силлогизме, необходимо брать истинные посылки, соблюдать правила фигур и не нарушать общие правила простого категорического силлогизма.

35) Умозаключение, посылки и заключение которого являются суждени­ями с отношениями, называется умозаключением с отношениями.

Например:

Петр — брат Ивана. Иван — брат Сергея.

Петр — брат Сергея.

Посылки и заключение в приведенном примере — суждения с от­ношениями, имеющие логическую структуру xRy, где х и у — понятия о предметах, R — отношения между ними.

Логическим основанием умозаключений из суждений с отноше­ниями являются свойства отношений, важнейшие из которых — 1) симметричность, 2) рефлексивность и 3) транзитивность.

1. Отношение называется симметричным (от греческого simmetria—«соразмерность»), если оно имеет место как между предметами х и у, так и между предметами у и х. Иначе говоря, перестановка членов отношения не ведет к изменению вида отношения. Симметричными являются отношения равенства (если а равно Ь, то и b равно а), сходства (если с сходно с d, то и d сходно с с ), одновременности (если событие х произошло одновременно с событием у, значит, и событие у произошло одновременно с событием х), различия и некоторые другие.

Отношение симметричности символически записывается:

XRy — yRx.

2. Отношение называется рефлексивным (от латинского reflexio — «отражение»), если каждый член отношения находится в таком же отношении к самому себе. Таковы отношения равенства (если а = Ь, тоа = аиЬ = Ь)и одновременности (если событие х произошло одновременно с событием у, значит, каждое из них произошло одновременно с самим собой).

Отношение рефлексивности записывается:

xRy -+ xRx Л yRy.

3. Отношение называется транзитивным (от латинского transitivus — «переход»), если оно имеет место между х и z тогда, когда оно имеет место между х и у и между у и z. Иначе говоря, отношение является транзитивным (переходным) тогда и только тогда, когда из отношения между х и у и между у и z следует такое же отношение между х и z.

Транзитивными являются отношения равенства (если а равно b и b равно с, то а равно с), одновременности (если событие х произошло одновременно с событием у и событие у одновременно с событием z, значит, событие х произошло одновременно с событием z), отноше­ния «больше», «меньше» (а меньше b, b меньше с, значит, а меньше с), «позднее», «находиться севернее (южнее, восточнее, западнее)», «быть ниже, выше» и т. п.

Отношение транзитивности записывается:

(xRy Л yRz) -* xRz.

Для получения достоверных заключений из суждений с отношени­ями необходимо опираться на правила:

Для свойства симметричности (xRy -* yRx): если суждение xRy ис­тинно, то суждение yRx тоже истинно. Например:

А подобно В. В подобно А.

Для свойства рефлексивности (xRy -+ xRx л yRy ): если суждение xRy истинно, то истинными будут суждения xRx и yRy. Например:

а = Ь. а = а и b = b.

Для свойства транзитивности (xRy л yRz -* xRz ): если суждение xRy истинно и суждение yRz истинно, то суждение xRz также истинно, Например:

К. был на месте происшествия раньше Л. Л. был на месте происшествия раньше М.

К. был на месте происшествия раньше М.

Таким образом, истинность заключения из суждений с отношени­ями зависит от свойств отношений и регулируется правилами, выте­кающими из этих свойств. В противном случае заключение может оказаться ложным. Так, из суждений «Сергеев знаком с Петровым» и «Петров знаком с Федоровым» не следует необходимого заключе­ния «Сергеев знаком с Федоровым», так как «быть знакомым» не яв­ляется транзитивным отношением.