
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объединенная классификация суждений по качеству и количеству.Содержание книги
Поиск на нашем сайте
1. Загальностверджувальне суждения - это суждения, которые по количеству является общим, а по качеству - утвердительным. Обозначается как А. Структура его: "Все S есть Р". Например, "Все люди... стремятся к знанию" (Аристотель). Субъект суждения - "люди", предикат - "стремятся к знанию". На то, что это суждение загальностверджувальним указывает: кванторного слово "все" - суждение общее, и связка "есть" (ее можно привести в явном виде - "есть теми, кто стремится со знание") - суждение утвердительное. 2. Частковостверджувальне суждения - это частичное по количеству и утвердительное по качеству суждения. Обозначается как И. Структура такого суждения: "Некоторые S есть Р". Например, "Некоторые металлы тонут в воде". Субъект - "металлы", предикат - "тонут в воде". Это суждение частковостверджувальним: кванторного слово "некоторые" - суждение частичное и логическая связка "есть" ("некоторые металлы являются, тонущие в воде") - суждение утвердительное. 3. Загальнозаперечне суждения - это суждение общее по количеству и отрицательное по качеству. Обозначается как Э. Структура: "Ни одно S не есть Р". Например, "Ни один лев не является травоядным". Субъект - "лев", предикат - "травоядный". На то, что суждение загальнозаперечним указывает: кванторного слово - "ни один" (суждение общее) и логическая связка - не (суждение по качеству является отрицательным). 4. Частковозаперечне суждения - это суждения частичное по количеству и отрицательное по качеству. Обозначается как А. Структура: "Некоторые S не есть Р". Например, "Некоторые учебники не содержат интересной информации". Субъект - "учебники", предикат - "содержат интересную информацию". Суждения частковозаперечне на что указывает: кванторного слово "некоторые" и логическая связка "не есть".
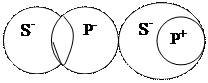
Распределенность терминов в категорических суждениях. Срок считается распределенным (обозначается +), если его объем полностью включается или полностью исключается из объема другого термина. Срок считается нераспределенной (обозначается -), если его объем частично включается или частично исключается из объема другого термина. Проанализируем типичные случаи. Суждения А. "Все S есть Р". 1. Все адвокаты (S) являются юристами (Р). Субъектом этого суждения является "адвокаты", предикатом - "юристы". Субъект является распределенным, так как речь едет о всех адвокатов. Для того, что быть адвокатом необходимо иметь юридическое образование, то есть объем понятия «адвокат» полностью включается в понятие "юрист". Сущность не является распределенным, поскольку в нем содержится только часть "юристов", которые являются адвокатами. Распределенность терминов можно проиллюстрировать с помощью кругов Эйлера. Для данного примера рассмотрим рисунок 1.
Малюнок 1 Малюнок 2 Малюнок 3. Малюнок 4. 2. М. Булгаков (S) является автором романа "Мастер и Маргарита" (Р). Субъектом суждения является понятие "М. Булгаков "(подчеркиваем и обозначаем как S), предикатом - автор романа" Мастер и Маргарита "(обозначаем в суждении как Р). Это загальностверджувальне суждения. Обозначаем как А. Субъект и предикат являются распределенными, поскольку их объемы полностью совпадают (рис. 2). Суждения И. "Некоторые S есть Р". 1. Некоторые врачи (S) шахматисты (Р). Субъектом суждения есть врачи (обозначаем, подчеркиваем), предикатом - "шахматисты" (обозначаем, подчеркиваем). Квантор - "некоторые". Субъект является нераспределенной, поскольку в нем понимается только часть врачей (те врачи, увлекающихся шахматами), т.е. объем субъекта лишь частично включается в объем предиката. Предикат тоже не является распределенным, поскольку тоже включается в объем субъекта лишь частично - только часть шахматистов являются врачами (рисунок 3). 2. Некоторые юристы (S) являются адвокатами (Р). Субъект суждения - юристы, предикат - адвокаты (это свойство мы приписываем субъекту). Субъект суждения не является распределенным, поскольку в нем понимается только часть юристов, те юристы, которые являются адвокатами. Предикат является распределенным, поскольку объем предиката полностью включается в объем субъекта - адвокат должен быть юристом (рисунок 4). Суждения Е. "Ни один S не есть Р". Никто (S) не является бессмертной (Р). Субъект суждения - человек, предикат - быть бессмертным. Субъект и предикат являются распределенными, поскольку объем субъекта полностью исключается из объема предиката - никто не относится к бессмертных существ, и наоборот. Рисунок 5.
Малюнок 5. Малюнок 6. Малюнок 7. Суждения А. "Некоторые S не есть Р". 1. Некоторые растения (S) не являются лекарственными растениями (Р). S - растения, Р - лекарственные растения (обозначаем, подчеркиваем). Субъект не является распределенным, поскольку понимается лишь часть растений, те растения, которые являются лекарственными. Предикат является распределенным, поскольку объем понятия "лекарственные растения" полностью включается в понятие "растения". Рисунок 6. 2. Некоторые студенты (S) не является музыкантами (Р). Субъект - студенты, предикатом является понятие "музыканты". Субъект не является распределенным, поскольку нас интересует часть студентов, которые не являются музыкантами. Предикат является распределенным, поскольку остается в полном объеме. Рисунок 7.
2. Примеры. Для того, чтобы дать логический анализ простого категорического суждения, необходимо: 1. Выяснить структуру суждения: субъект, предикат, логическую связи. 2. Определить вид суждения. 3. Записать логическую форму (схему) суждения. 4. Зарисовать соотношение между терминами суждения в кругах Эйлера. 1. Ни одна звезда не является планетой. а) Субъект суждения - звезда (подчеркиваем, обозначаем S), предикатом суждения является понятие "планета" (подчеркиваем, обозначаем Р). Ни одна звезда (S) не является планетой (Р). б) Это суждение - загальнозаперечне: "ни один" - является квантором всеобщности, а логическая связка "не является" указывает на отрицательный характер суждения. Обозначим суждения. Логическая схема: Ни один S не есть Р (Е) Ни звезда (S) не является планетой (Р). в) Находим соотношение между терминами суждения и указываем распределенность терминов. В данном случае сроки полностью исключают друг друга, т.е. оба термина являются распределенными и этому соответствует рисунок 5. 2. Большинство вулканов не угасли. а) Находим субъект и предикат суждения, обозначаем и подчеркиваем сроки суждение: "Большинство вулканов (S) не погасли (Р)". б) Устанавливаем тип суждения. Кванторного слово "большинство" указывает на то, что нас интересует не весь субъект, а часть субъекта, часть вулканов, то есть по количеству это суждение - частное. Логическая связка, которая не приведена в явном виде ("Большинство вулканов не являются вулканами, что погасли"), "не является" указывает на то, что суждение отрицательным по качеству. Суждение частковозаперечним - А. Логическая схема: Некоторые S не есть Р. Обозначим тип суждения. (О) "Большинство вулканов (S) не погасли (Р)". в) Находим соотношение между терминами суждения и указываем распределенность терминов. Субъект не является распределенным, поскольку в данном суждении указывается лишь часть субъекта (большинство вулканов); предикат является распределенным, поскольку объем понятия "же вулканы потухли" полностью включается в понятие "вулканы". Этому соответствует рисунок 6.
3. Задания для самостоятельного выполнения. 1.1. Укажите кванторного слова и логическую связи суждение если указан тип суждения: 1. (Е)... кролик... хищное животное 2. (А)... соболя... ценные пушные звери 3. (I)... животные... водоплавающие 4. (Е)... океан... пресноводным 5. (О)... спортсмены... чемпионами Олимпийских игр 6. (I)... ягоды... ядовитые 7. (Е)... картофель... ананас 8. (О)... вулканы... такими, что погасли 9. (I)... преступники... невменяемыми 10. (О)... истины... опровергнуть 1.2. Найдите субъект, предикат, укажите тип суждения, найдите соотношение между терминами и зарисуйте их в кругах Эйлера. 1. Некоторые животные делают запасы на зиму 2. Все ежи являются колючими 3. Везувий - это действующий вулкан 4. Некоторые тела легче воды 5. Озеро Виктория не находится в США 6. Ни один химический элемент не является сложной веществом 7. Некоторые млекопитающие не различают цвета 8. Он был невысоким 9. Некоторые народы не находятся в неволе 10. Все, кроме одного, студенты нашей группы получили высокие баллы
2.2. логический квадрат 1. Теоретичні відомості Відношення між простими атрибутивними судженнями – А, Е,
у вигляді “логічного квадрату”. Літери, що знаходяться у кутах квадрата, позначають види суджень, а сторони та діагоналі - усі можливі І О відношення між судженнями.
Отношение подчинения-это отношение между такими суждениями с одинаковыми субъектами и предикатами, в которых количество различно, а качество то же самое. В таком отношении находятся суждения А - И, а также Е - О. При этом действуют следующие закономерности: 1) Из истинности суждения типа А (или Е) с необходимостью следует вывод об истинности суждения и (или О). Например, если известно, что суждения типа А: "Все слоны - млекопитающие" являются истинными суждением, то и суждения И "Некоторые слоны - млекопитающие" является истинным. Внимание! Но следует отметить, что истинность частичного суждения оставляет общее суждение неопределенным: оно может быть как истинным, так и ложным (при нарушении этого правила может возникнуть логическая ошибка - "поспешное обобщение"). Например, если истинно, что "Некоторые кролики - белые" (суждения I), то остается неопределенным общее суждение А: "Все кролики - белые". 2) С ложности частичного суждения (I или О) с необходимостью следует вывод о ложности общего суждения (А или Е). Например, если известно, что суждение О: "Некоторые дельфины не являются млекопитающими" ошибочно, то общее суждение (Е): "Все дельфины не являются млекопитающими" ошибочно также. Внимание! Следует отметить, что ошибочность общего суждения (А или Е) оставляет частичное суждение (I или О) неопределенным: оно может быть как истинным так и ложным. Например, если суждение (А): "Все кролики являются белыми" ложно, то это не значит, что частичное суждение (I): "Некоторые кролики являются белыми" тоже должно быть ложным, оно может быть истинным. Отношение противоречия между суждениями с одинаковыми субъектами и предикатами характеризуется тем, что суждения, которые находятся в этом отношении, не могут быть ни одновременно истинными, ни одновременно ложными, знание истинности одного из них свидетельствует об ошибочности второго, а знание ложности одного из них - об истинности второго. Отношение противоречия имеет место между суждениями: А - О, Е - И. Например, если суждение "Все планеты Солнечной системы движутся вокруг Солнца" (А) является истинным, то противоречащее ему суждение О "Некоторые планеты Солнечной системы не движутся вокруг Солнца" является ложным. Если известно, что суждение Е "Ни один паук не является насекомым" является истинным, то противоречащее ему суждение И "Некоторые пауки являются насекомыми" ошибочно. Отношение противоположности (контрарности) (между суждениями (с одинаковыми S и Р) А - Е) характеризуется тем, что суждения, которые находятся в этом отношении, не могут быть одновременно истинными, но могут быть одновременно ложными. Отсюда вытекают следующие выводы: 1) если одно из суждений оказывается истинным, то второе непременно будет ложным, поскольку оба они одновременно не могут быть истинными, 2) если одно из суждений будет ложно, то сделать вывод (чисто логический, не считая реального положения вещей) о втором невозможно, поскольку оба эти суждения могут быть ошибочными. Второе суждение остается неопределенным. Другими словами: ложность одного из контрарных суждений показывает, что второе принадлежит или к ошибочным (поскольку А - Е могут быть одновременно ложными), или к истинным. Например, если известно, что суждение "Все рыбы дышат жабрами" (А) является истинным, то контрарных суждения (Е) "Ни одна рыба не дышит жабрами" является ошибочным. Если известно, что суждение (А) "Все студенты являются отличниками" ошибочно, то суждение (Е) "Ни один студент не является отличником" может быть как, к сожалению, истинным, так и ложным (некоторые студенты могут быть отличниками). Отношение пидпротивности (субконтрарности) (отношение между суждениями И - О) характеризуется тем, что субконтрарни суждения с одинаковыми субъектами и одинаковыми предикатами не могут быть одновременно ложными, но могут быть одновременно истинными. Таким образом, если суждение И ложно, то соответствующее суждение О есть непременно истинным. Однако с истинности суждения И не следует вывод ни о истинность, ни о ложности суждения А. Это касается и выводов из информации о суждениях А. Например, если известно, что суждения и "Некоторые студенты нашей группы являются отличниками" истинно, то суждение О "Некоторые студенты нашей группы не являются отличниками" является неопределенным, поскольку оно может быть как истинным, так и ложным. Если известно, что суждение О "Некоторые свидетели не говорят правду" ошибочно, то суждение И "Некоторые свидетели говорят правду" является истинным.
2. Примеры Проверьте логическую способность следующих суждений с помощью "логического квадрата". Укажите, в каких примерах допущены ошибки и в чем они заключаются. 1. Верно, что все совы - птицы, значит неверно, что некоторые совы не является птицами. Первое суждение загальностверджувальним (А), второе - частично-отрицательным (О). Отношения между этими суждениями называется отношение противоречия и заключается в том, что эти два суждения не могут быть одновременно ни истинными, ни ложными: если одно из них истинно, то второе будет ложным и наоборот. Суждение А по условиям нашей задачи является истинным, а суждение О - ложным (неверно, что...), поэтому вывод является верным. 2. Верно, некоторые цветы - розы, значит, неверно, что некоторые цветы не является розами. Первое суждение "Некоторые цветы - розы" является частично-утвердительным (I), второе суждение "Некоторые цветы не является розами" - частичной-возаперечним (О). Отношения между этими суждениями - пидпротивности (или субконтрарности). Известно, что субконтрарни суждения не могут быть одновременно ложными, но могут быть одновременно истинными. Таким образом, если известно, что суждения и является истинным, то сделать вывод (чисто логический, не считая реального положения вещей) о втором суждения О невозможно, поскольку оба эти суждения могут быть истинными, а также может вторым суждения О может оказаться ложным. Поэтому чисто логический вывод, сделанный с помощью логического квадрата имеет неопределенный характер. 3. Неверно то, что все дороги ведут в Рим, значит неверно то, что некоторые дороги ведут в Рим. Первое суждение загальностверджувальним (А), второе - частично-утвердительным (I). Отношения между этими суждениями является отношением подчинения. При этом действует такая закономерность (см. теоретическую часть): ложность общего суждения (А) оставляет частичное суждение (I) неопределенным: оно может быть как истинным так и ложным. Поэтому чисто логический вывод, сделанный с помощью логического квадрата имеет неопределенный характер. 4. Истинно, что все киты не является рыбами, выходит, что неверно, что некоторые киты - рыбы. Первое суждение - загальнозаперечне (Е), второе суждение - частично-утвердительное (I). Отношения между этими суждениями - это отношение противоречия, которое заключается в том, что эти отношения не могут быть одновременно ни истинными, ни ложными: если одно из них истинно, то другое непременно будет ложным, и наоборот. Поэтому вывод является верным. 5. Неверно, что ни один страус не является птицей, значит, верно, что все страусы - птицы. Первое суждение загальзаперечним (Е), второе - загальностверджувальне (А). Отношения между этими суждениями называется отношение противоположности (контрарности). Если одно из противоположных суждений ложное (в нашем случае суждения Е), то сделает вывод (чисто логический, не считая реального положения вещей) о втором суждения А невозможно, поскольку оба эти суждения могут быть ошибочными. Суждения А неопределенным, поскольку, по правилам "логического квадрата" оно может быть как истинным, так и ложным. 3. Неверно то, что все дороги ведут в Рим, значит неверно то, что некоторые дороги ведут в Рим. Первое суждение загальностверджувальним (А), второе - частично-утвердительным (I). Отношения между этими суждениями является отношением подчинения. При этом действует такая закономерность (см. теоретическую часть): ложность общего суждения (А) оставляет частичное суждение (I) неопределенным: оно может быть как истинным так и ложным. Поэтому чисто логический вывод, сделанный с помощью логического квадрата имеет неопределенный характер. 4. Истинно, что все киты не является рыбами, выходит, что неверно, что некоторые киты - рыбы. Первое суждение - загальнозаперечне (Е), второе суждение - частично-утвердительное (I). Отношения между этими суждениями - это отношение противоречия, которое заключается в том, что эти отношения не могут быть одновременно ни истинными, ни ложными: если одно из них истинно, то другое непременно будет ложным, и наоборот. Поэтому вывод является верным. 5. Неверно, что ни один страус не является птицей, значит, верно, что все страусы - птицы. Первое суждение загальзаперечним (Е), второе - загальностверджувальне (А). Отношения между этими суждениями называется отношение противоположности (контрарности). Если одно из противоположных суждений ложное (в нашем случае суждения Е), то сделает вывод (чисто логический, не считая реального положения вещей) о втором суждения А невозможно, поскольку оба эти суждения могут быть ошибочными. Суждения А неопределенным, поскольку, по правилам "логического квадрата" оно может быть как истинным, так и ложным. (А) Усі S є Р
Увага! Не слід забувати про зміну предикату!
(Е) Жоден вовк (S) не є не хижою твариною (не-Р)
2. загальнозаперечне суждения Е превращается в обще-утвердительное суждение А. Схема преобразования:
Приклад: (Е) Жоден вовк (S) не є травоїдним (Р)
3. частковостверджувальне суждения и превращается в частично-отрицательное суждение А. Схема преобразования:
(І) Деякі S є Р
Приклад: (І) Деякі числа (S) – прості (Р)
4. частковозаперечне суждения О превращается в частично-утвердительное И. Схема преобразования:
(О) Деякі S не є Р
Приклад: (О) Деякі книги (S) не є цікавими (Р)
Обращения. Обращение - это такое непосредственное умозаключение в результате которого субъект и предикат меняются местами, при этом субъект посылки становится предикатом заключения, а предикат посылки - субъектом заключения. В результате операции обращения качество суждения сохраняется, а количество может измениться. Осуществляя обращения, необходимо соблюдать требования равенства объемов терминов: объемы сроков заключения должны равняться объемам соответствующих терминов посылки. Традиционно различают два вида обращения: простое (или чистый) и обращения с ограничением. Если не меняется количество суждения, то обращение будет чистым или простым. Оно бывает тогда, когда оба термина исходного суждения (субъект и предикат) являются распределенными или оба термина не являются распределенными. Обращение с ограничением бывает тогда, когда изменяется количество исходного суждения, т.е. изменяется кванторного слово (например, кванторного слово "все" меняется на "некоторые"). Это происходит для того, чтобы не нарушить требования равенства объемов терминов. 1. Суждения А может вращаться как чисто, так и с ограничением. а) чистое или просто обращение происходит при равенстве объемов S и Р, например, в определениях. Суждение А вращается в суждение А. Схема обращения:
(А) Усі S є Р
(А) Усі рівносторонні прямокутники (Р) є квадратами (S) б) обернення з обмеженням відбувається коли суб’єкт вихідного судження є розподіленим, а предикат – нерозподіленим. Судження А обертається в судження І. Схема обернення:
(І) Деякі Р є S Приклад: (А) Усі дельфіни (S) є ссавцями (Р)
2. загальнозаперечне судження Е обертається в загальнозаперечне судження Е. Оскільки в загальнозаперечном судженні Е суб’єкт і предикат є розподіленими, то обернення буде чистим або простим. Схема обернення: (Е) Жоден S не є Р
Приклад: (Е) Жоден плазун (S) не літає (Р)
3. частковостверджувальне судження І також може обертатися як чисто, так і з обмеженням: а) просте обернення відбувається при нерозподіленності термінів S і Р, судження І обертається в судження І. Схема обернення: (І) Деякі S є Р
Приклад: (І) Деякі вчені (S) – митці (Р)
б) коли обсяг Р менше за обсяг S, тобто Р є розподіленим, а S – не розподіленим, то відбувається обернення з обмеженням, зі зміною кванторного слова “деяке” на “всі”. Частковостверджувальне судження І обертається на загальностверджувальне судження А. Схема обернення: (І) Деякі S є Р
(А) Всі композитори (Р)– музиканти (S) 4. частковозаперечне суждения О не вращаются. Субъект в таких суждениях не является распределенным, значит, он не может стать предикатом нового, тоже отрицательного суждения, где предикат всегда распределенным. Применив операцию обращения к частковозаперечних суждений, мы не получим необходимого вывода. Так, например, с истинного частковозаперечного суждения "Некоторые животные не являются львами" путем обращения невозможно получить истинное суждение. Противопоставление предикату Противопоставление предикату - это такое непосредственное умозаключение, в ходе которого осуществляется сначала преобразование, а затем обращения суждения. При Противопоставление предикату субъект посылки (исходного суждения) становится предикатом заключения, а субъектом заключения выступает понятие, противоречащее предикат посылки. То есть мы выполняем следующую последовательность действий: 1. сначала делаем преобразования - Логическую связи меняем на противоположную; - Вместо предикату Р берем не-Р; 2. делаем операцию обращения: меняем местами S и не-Р; Противопоставление предикату для различных видов суждения: 1. Загальностверджувальне суждения А перестраивается по схеме: Першій крок: (А) Усі S є Р; далі перетворення (Е) Жоден S не є не-Р; далі обернення: (Е) Жодне не-Р не є S. Схема протиставлення: (А) Усі S є Р
Приклад (Усі приклади розглядаються як послідовне виконання операцій перетворення і обернення): (А) Усі леви (S) – ссавці (Р) (Е) Жоден лев (S) не є не-ссавцем (не-Р)
2. Загальнозаперечне судження Е перебудовується в судження І: 1. (Е) Жоден S не Р; 2. (А) Усі S є не-Р; 3. (І) Деякі не-Р є S. Схема:
(І) Деякі не-Р є S
Приклад: (Е) Жодна планета (S) не є зіркою (Р) (А) Усі планети (S) є не-зірками (не-Р)
3. Частковозаперечне судження О перебудовується в судження І: 1. (О) Деякі S не є Р; 2.(І) Деякі S є не-Р; 3. (І) Деякі не-Р є S. Схема: (О) Деякі S не є Р
Приклад: (О) Деякі гриби (S) не є отруйними (Р) (І) Деякі гриби (S) є не-отруйними (не-Р)
4. Із частковостверджувального судження І необхідні висновки не випливають. 1. (І) Деякі S є Р; 2. (О) Деякі S не є не-Р; 3. Судження О не обертаються. 2. примеры 1. Сделает преобразования: 1. Некоторые млекопитающие не являются хищниками. Находим субъект и предикат суждения, обозначаем их; устанавливаем тип суждения. (О) Некоторые млекопитающие (S) не являются хищниками (Р) При преобразованы изменяется качество посылки без изменения ее количества, при этом предикат вывода является отрицанием предиката посылки. То есть надо изменить качество суждения (логическую связи "не есть" на "е") и при этом помнить, что предикат суждения тоже меняется: (I) Некоторые млекопитающие (S) не-хищниками (не-Р). Есть частковостверджувальне суждения. Итак, (О) Деякі ссавці (S) не є хижаками (Р)
2. Знаходимо суб’єкт та предикат, позначаємо їх; встановлюємо тип судження: (А) Усі жирафи (S) мають довгу шию (Р)
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.132.80 (0.011 с.) |


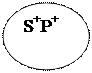



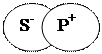


 А Е І, О – для наочності зображають графічно
А Е І, О – для наочності зображають графічно (Е) Жоден S не є не -Р
(Е) Жоден S не є не -Р Приклад: (А) Усі вовки (S) – хижі тварини (Р)
Приклад: (А) Усі вовки (S) – хижі тварини (Р) (Е) Жоден S не є Р
(Е) Жоден S не є Р
 (А) Усі вовк (S) є не-травоїдним (не-Р)
(А) Усі вовк (S) є не-травоїдним (не-Р) (О) Деякі S не є не-Р
(О) Деякі S не є не-Р (І) Деякі S є не-Р
(І) Деякі S є не-Р
 (А) Усі Р є S
(А) Усі Р є S Приклад: (А) Усі квадрати (S) є рівносторонніми прямокутниками (Р)
Приклад: (А) Усі квадрати (S) є рівносторонніми прямокутниками (Р) (А) Усі S є Р
(А) Усі S є Р (І) Деякі ссавці (Р) є дельфінами (S)
(І) Деякі ссавці (Р) є дельфінами (S) (Е) Жоден Р не є S
(Е) Жоден Р не є S (Е) Жоден з літаючих (Р) не належить до плазунів (S)
(Е) Жоден з літаючих (Р) не належить до плазунів (S) (І) Деякі Р є S
(І) Деякі Р є S
 (А) Усі Р є S
(А) Усі Р є S (Е) Жоден не-Р не є S
(Е) Жоден не-Р не є S (Е) Жоден не-ссавець (не-Р) не є левом (S)
(Е) Жоден не-ссавець (не-Р) не є левом (S) (Е) Жоден S не є Р
(Е) Жоден S не є Р (І) Деякі не-зірки (не-Р) є планетами (S)
(І) Деякі не-зірки (не-Р) є планетами (S) (І) Деякі не-Р є S
(І) Деякі не-Р є S (І) Деякі не-отруйні (не-Р) є грибами (S)
(І) Деякі не-отруйні (не-Р) є грибами (S) (І) Деякі ссавці (S) є не- хижаками (не-Р)
(І) Деякі ссавці (S) є не- хижаками (не-Р)


