
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение изменчивости оценок критериевСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
С применением энтропии
1. Сформируем матрицу принятия решений
2. Проведем нормировку P =>
где i = 0≤ 3. Определим уровень энтропии
4. Уровень изменчивости
5. Определим
6. Если имеется экспертная оценка
Упорядочение альтернатив методом перестановок При применении этого метода проверяются все перестановки альтернатив по предпочтительности и сравниваются между собой. 1. Составление исходной матрицы принятия решения P={ 2. Назначение весовых коэффициентов для критериев
3. Построение вариантов всевозможных перестановок πg =
4. Построение множества номеров критерия (для каждой пары альтернатив), значения которых согласуются с порядком альтернатив рассматриваемой перестановки
5. Построение множества номеров критериев (для каждой пары альтернатив), значения которых не согласуются с порядком рассматриваемых перестановок
6. Определение оценки каждой перестановки альтернатив согласно выражению:
7. Упорядочиваем перестановки по убывания. Перестановка с максимальным Преимущества: - могут быть использованы оценки критериев (в ранговых шкалах). Недостатки: - сложность алгоритма n!; - сложность оценки системы предпочтения; - результат получен в ранговой шкале.
Пример выполнения лабораторной работы Лабораторная работа №1 Методы принятия решений: «смещённого идеала» и перестановок
Цель работы: изучение основных алгоритмов метода «смещённого идеала» и перестановок. Постановка задачи: провести ранжирование альтернатив выбранной предметной области методом «смещённого идеала» и методом перестановок. Предварительно сформировать множество Эджворта-Парето. Матрица принятия решений – 4x4. При определении важности критериев учитывать степень изменчивости их оценок. Сравнить полученные результаты. Содержание отчёта 1. Назначение и цель лабораторной работы. 2. Постановка задачи в соответствующей предметной области. 3. Полученные результаты. Выводы. Пример выполнения Предметная область – пылесосы. Критерии – мощность, ёмкость пылесборника – мажорируемые, вес, цена – минорируемые. Альтернативы: 1. Bosch BSG 82425; 2. Electrolux Z 8810 UltraOne; 3. Samsung SC6530; 4. Zelmer Aquawelt 919.0 ST. Исходные данные
Альтернативы соответствуют множеству Эджворта-Парето. Важность критериев (экспертная оценка)
Шаг №1. Матрица принятия решений (x):
1. Идеальный и неидеальный объекты:
2. Переход к относительным единицам (d):
3. Определение комплексной важности: А) Матрица принятия решений:
Б) Нормированная матрица принятия решений (p):
В) Энтропия (Е):
Г) Инвертированная энтропия (l):
Д) Комплексная важность (
P1: S1>S3>S2>S4 P2: S1>S3>S2>S4 P3: S1>S3>S2>S4 P4: S1>S3>S2>S4 P5: S1>S3>S2>S4 Найдена наихудшая альтернатива – S4. Исключаем её. Шаг №2. Матрица принятия решений (x):
1) Идеальный и неидеальный объекты:
2) Переход к относительным единицам (d):
3) Определение комплексной важности:
А) Матрица принятия решений:
Б) Нормированная матрица принятия решений (p):
В) Энтропия (Е):
Г) Инвертированная энтропия (l):
Д) Комплексная важность (
4) Определение расстояния от неидеального объекта до i-го:
5) Ранжирование альтернатив и отсеивание: P1: S1>S3>S2 P2: S1>S3>S2 P3: S1>S3>S2 P4: S1>S3>S2 P5: S1>S3>S2 Найдена наихудшая альтернатива – S2. Исключаем её.
Шаг №3. Матрица принятия решений (x):
1) Идеальный и неидеальный объекты:
2) Переход к относительным единицам (d):
3) Определение комплексной важности: А) Матрица принятия решений:
Б) Нормированная матрица принятия решений (p):
В) Энтропия (Е):
Г) Инвертированная энтропия (l):
Д) Комплексная важность (
4) Определение расстояния от неидеального объекта до i-го:
5) Ранжирование альтернатив и отсеивание: P1: S1>S3 P2: S1>S3 P3: S1>S3 P4: S1>S3 P5: S1>S3 Найдена наихудшая альтернатива – S3. Исключаем её. Результат – альтернатива №1 – Bosch BSG 82425.
Метод перестановок Матрица принятия решений (x):
Комплексная важность (
Для перестановки {S1 S2 S3 S4} 1) S1>S2 C=(1 2 3) H=(4) 2) S1>S3 C=(1 2) H=(3 4) 3) S1>S4 C=(1 2 4) H=(3) 4) S2>S3 C=(1) H=(2 3 4) 5) S2>S4 C=(1 4) H=(2 3) 6) S3>S4 C=(3 4) H=(1 2) Вес перестановки: B=1,22314
Веса всех перестановок:
Лучшая перестановка (с максимальным весом) – 1324. Получаем лучшую альтернативу S1 – Bosch BSG 82425. Лабораторная работа № 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.243 (0.009 с.) |

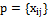
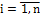
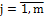
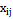 – оценка по j-ому критерию для i-ой альтернативы.
– оценка по j-ому критерию для i-ой альтернативы.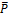
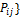
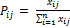 ,
, , j =
, j =  ,
, 
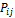 ≤1
≤1 для каждого критерия
для каждого критерия = -k
= -k 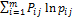 , где j=
, где j= 
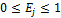
 =1-
=1-  , j=
, j=  , то комплексная важность критерия
, то комплексная важность критерия  , j=
, j=  , i=
, i=  , j=
, j= 
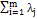 =1, j=
=1, j= 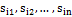 ∀g, g=
∀g, g= 
 >
> 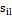 , если k>e
, если k>e
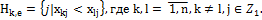
 , g=
, g= 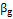 является наилучшей.
является наилучшей. ):
):


