Карти поняття і карти мислення

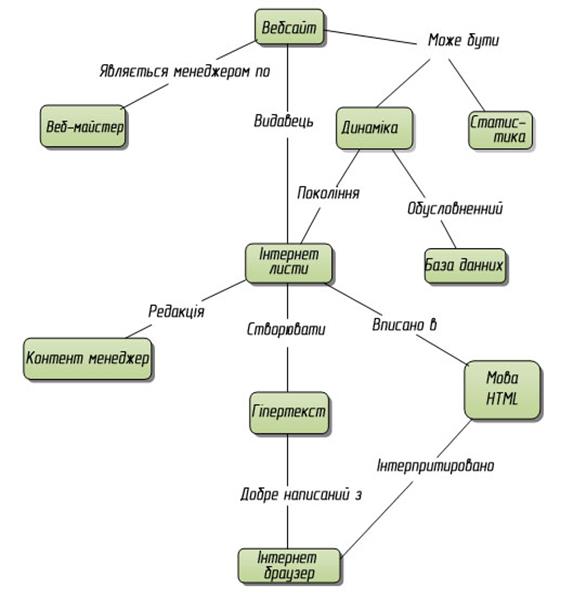
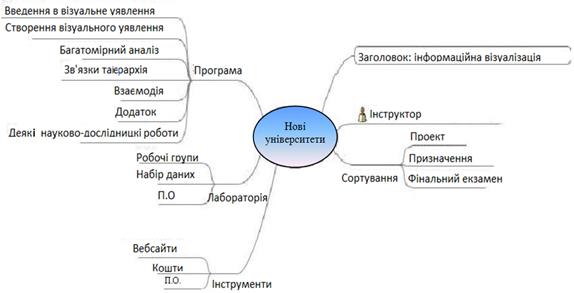
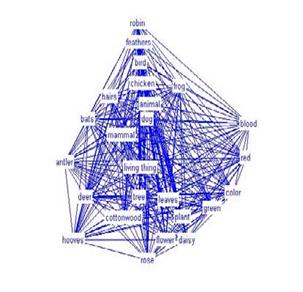
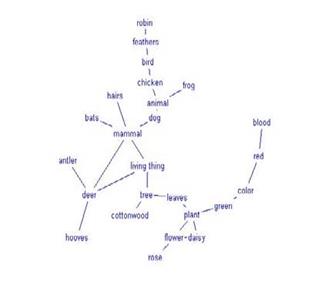
Карти поняття, запропоновані Джозефом Новеком на початку 1970 є об'єднанням синтаксису і морфології тобто певною граматикою уявлення, показуючи відносини серед понять складної і структурованої області. Вони побудовані з ряду понять (семантичні вузли), які продовжуються до їх зв'язків за допомогою маркірованих країв (думки), які описують тип зв'язку. Також можливо почати із загального доводу "проти", зв'язуючи це, поступово, з більш визначеним поняттями, і мати достатньо детальний опис області. Можливо створити карти для будь-якого типу даних: вебсайт, книга, обслуговування, продукт, і т.д. карти поняття краще всього використовуються в навчанні, оскільки їм вдається змальовувати у загальних рисах структуроване знання в дуже синтетичній і аргументованій манері. Рис. 2.25 зображає карту поняття, що описує поняття "вебсайта".

Карти мислення подібні картам поняття. Вони використовуються, щоб описати ідеї, ситуації, проекти, організації, і т.д. графічними асоціаціями. Вони знаходять багато застосувань в сесії мозкової атаки, в освітньому просторі, навколишньому середовищі, або організації ідеї. Наприклад, відвідуючи урок для уявлення, потрібна ефективна мнемонічна і організаційна техніка що складається з розгляду найважливіших понять в графічно-текстовій манері і з'єднанні їх один з одним, графічно, через логічно-асоціативні відносини. Карти мислення звичайно організовуються, починаючи з центрального поняття. Потім з нього випускаються більш корельовані вузли, які будуть далі спеціалізовані і розділені. Відрізняє, карту розуму від карти поняття, факт наявності єдиної теми що як відправна крапка (в протилежність картам поняття, у яких може бути багато початків). Наявність радіальної структури, де вузли розвиваються від основного предмету, згідно багатьом рівням, тоді як карти поняття засновані на зв'язках між поняттями. Приклад карти розуму, яка представляє початкові ідеї для підготовки університетського курсу, ілюстрований в рис. 2.26.

Рис 2.25 Карта поняття, яка описує поняття вебсайта.

 

Тоні Бузене, англійський дослідник, який вводив термін “карта розуму," спробував теоретизувати цей підхід, проектуючи багато правил і передового досвіду, щоб використовувати карту розуму, таку як використовування кольорів, зображень, символів, і різних розмірів.

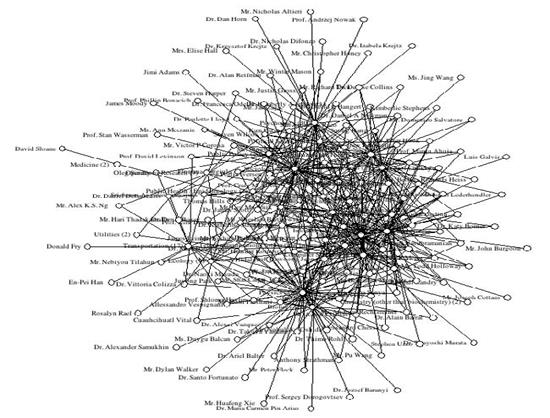
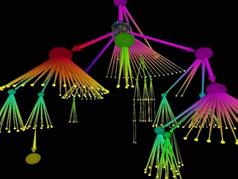
Рис. 2.26 Карта розуму для планування університетського курсу.

Складні дані мережі

Графи - дуже ефективна форма уявлення для даних мережі, але на жаль у них є незручність від того, що вони слабо масштабуються: збільшуючи число вузлів, граф стає дуже складним і не дуже легким для читання. Граф на рис. 2.27 описує мережу соціальних відносин серед багатьох людей. Кожен вузол представляє людину, тоді як краї представляють соціальні відносини серед цих людей, таких як сім'я, друзі, колеги, або знайомі.

Візуальне уявлення цього типу, назване соціальними мережами, важливе щоб зрозуміти соціальні відносини серед різних людей, і визначити якісні аспекти, такі як лідерство або появу неофіційних структур. Проблема уявлення в цьому випадку - густина вузлів і країв, сконцентрованих в маленькому місці, яка позбавляє можливості розрізняти їх серед графічних елементів, поміщених в центр.

Дослідження щодо проблеми складних графів продовжуються.

Періодично, пропонуються нові методології, щоб збільшити число значущих вузлів - в графі, або для поліпшення їх чіткості. Цими проблемами можна зайнятися, приймаючи одну з наступних стратегій:

• використовування нових геометричних заходів (розташування) для проекту графа, щоб забезпечити легкість для читання

• наближаючи структуру із зменшеним, але більш легким для читання, графом, скорочуючи кількість зв’язків показаних на графі або приховуючи не істотні відносини після того, як вони показані

• додавання до програмного забезпечення, яке надає візуальні уявлення, щоб задати динамічні графи, якими можна управляти і досліджувати згідно потребам користувача.

Рис 2.27 Складний граф соціальних відносин

 

Інтерактивні методи активно розвиваються. Далі розглянуті деякі приклади того, як були застосовані геометричні заходи і наближення, щоб надавати легші для читання графи.

 

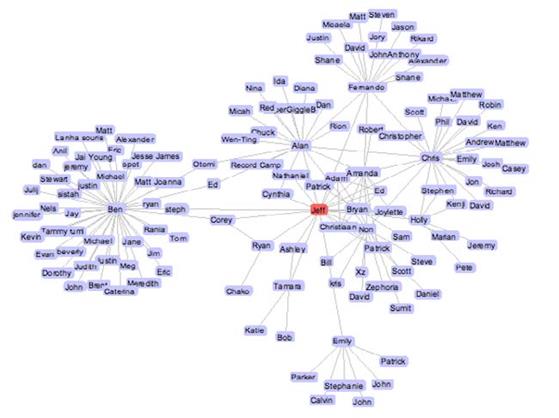
Оптимізація розташування

Основна проблема в представленні графа з дуже великою кількістю вузлів полягає в тому, що у них часто є така велика кількість країв, які перетнулися, що для користувча стає не можливим відчувати загальну структуру графа. Ідеал повинен був би влаштувати вузли в місці, щоб мінімізувати число країв, які перетнулися. Найзагальніші методи розташування, які намагаються оптимізувати розташування вузлів, використовують алгоритми, які поміщають вузли графа в двох - або тривимірний простір так, щоб всі краї мали більш менш рівну довжину і є краями, що трохи, наскільки можливо перетнулися. У графа, що виходить, також є добрі естетичні властивості (однорідна довжина краю, однорідний розподіл краю, і деяка симетрія). Рис. 2.28 представляє граф, створений інструментом Джеффрі Хира, який показує соціальну сіть, що використовує направлений алгоритм.

Скорочення складності графа

Коли число вузлів є дуже великим (як структура даних з десятками вузлів), геометричні методи також показують свої межі, і для зменшеного місця на екрані, для складності алгоритмів розташування, більш довгий час обчислення. Можливість, що ми маємо при візуалізації графа, який міг бути корисним користувачу, полягає в тому, щоб створити "зменшену версію" графа. Порівняння з скороченою версією, яка жертвує інформацією, але одночасно закінчує тим, що була більш легкою для читання і тримає глобальну структуру даних, дозволяючи ідентифікацію головних ознак. Щоб добре врахувати заключне візуальне представлення графа, необхідно спробувати скоротити кількість представлених об'єктів і, в той же самий час, зберегти глобальну структуру графа (який звичайно є головним цікавим місцем для аналізу). Дуже проста технологія, названа скороченням зв'язку, складається з візуалізації тільки країв, що мають вагу вище певної цінності, якщо це задовольняє певним критеріям. Таким чином, тільки краї, які могли представляти інтерес для користувача будуть представлені.

Рис 2.28 Граф який використовує алгоритм, представлення соціальної мережі.

Інші, складніші методи, такі як мінімальні дерева обхвату аналізують топологічну структуру вузлів і країв, щоб усунути надмірні краї і підтримати найістотніші зв'язки. Уявлення в рис. 2.29 повний (залишений) граф і його зменшена версія (праворуч).

Щоб зменшити складність графа, можна також втрутитися, намагаючись зменшити число вузлів, що візуалізуються. Так групують методи, які можуть бути застосовані до даних, які будуть представлені графами. Ці методи мають тенденцію візуалізувати групу "подібних вузлів", комбінуючи їх в одному вузлі (група), щоб скоротити кількість вузлів і країв, які візуалізуватимуться. Ступінь "подібності між двома вузлами залежить від" прикладного типу і області даних, що візуалізуються через граф.

 

Деякі рішення були вивчені для виробництва і управління графами з надзвичайно високим числом вузлів. Ці рішення використовують комбінуючи методи розташування, наближення, і взаємодії. Один з їх, Niche Works, в змозі розглядати до мільйона вузлів через декілька хвилин.

Рис 2.29 Повній граф і зменшена версія зв'язку.

Велика кількість вузлів, що відноситься до області. Niche Works використовує радіальне позиціонування, щоб оптимізувати розташування вузлів в місці, на шляху, який уникає країв, що перетнулися, і визначає високий номер вузлів у видимому місці. Крім того, вага, пов'язана з краями, врахована в конструкції графа, так, щоб вузли були поміщені на відстані, обернено-пропорційно вагам країв, які сполучають їх. Рис. 2.30 показує три типи розташувань, запропоновані Niche Works:

• Кругле розташування. Вузли влаштовані циркулярно в безпосередній периферії єдиного круга.

• Шестикутна сітка. Вузлі влаштовані в пунктах регулярної шестикутної сітки.

Рис. 2.30Головні розташування NicheWorks: проспект, шестикутний (центр), і дерево (праворуч).

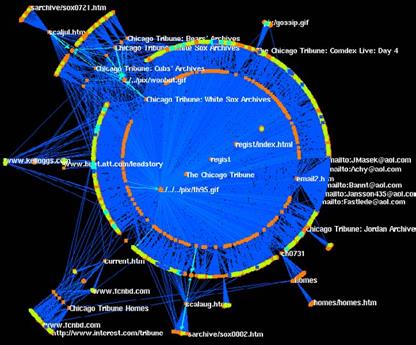
Рис. 2.31 NicheWorks показує граф структури вебсайта Chicago Tribune.

• Розташування дерева. Вузли влаштовані з вузлом коріння в центрі, навколо якого кожен вузол влаштований на крузі. Цей тип розташування є відповідним для ієрархічних структур, але також може бути застосований, щоб передати дані.

NicheWorks використовувався, щоб вивчити шахрайські міжнародні телефонні дзвінки і проаналізувати складні структури вебсайта. Рис. 2.31 показує граф структури сторінок і внутрішніх посилань,, вебсайта Chicago Tribune, однієї з головних щоденних газет Чикаго. Мета уявлення полягає в тому, щоб зрозуміти, як вебсайт був структурований і бачити, які критерії розрахунку використовувалися в його виробництві. Граф був уявлений, використовуючи розташування дерева. У формі і кольорах вузлів є наступна картографія:

• оранжевий квадрат: місцеві сторінки

• оранжевий круг: місцеві зображення

• синій квадрат: зовнішні сторінки

• жовтий квадрат: інтерфейс програми для того, щоб управляти формами або динамічними сторінками.

Деякі з найважливіших рис у маркіровані розглянуті нижче. Граф показує вхідні сторінки ділянки (розміщений в центрі) як зв'язок з місцевою сторінкою. Ці сторінки містять зв'язок з подальшими динамічними сторінками (зовнішній круг). Тому, структура трьох рівнів (головна сторінка вебсайта, внутрішній круг, і зовнішній круг) глобально домінує. Тільки у обмеженого числа сторінок є різна структура, яка є головним чином сторінками, що мають справу із спортивними темами.

Перевага підходів, заснованих на візуальних уявленнях, у протилежність автоматичним методам аналізу, таким як алгоритми пошуку даних використовують, їх гнучкість і здатності людської візуальної системи пристосуватися. Згідно авторам NicheWorks], люди, які намагаються обдурити телефонні компанії, використовують системи, які ухиляються від систематичних перевірок, що виконані на міжнародних дзвінках. Використовування систем візуалізації може натомість бути пристосоване динамічно до низького визнання можливих змін, які тоді використовуються злочинцями в цих зловживаннях.

 

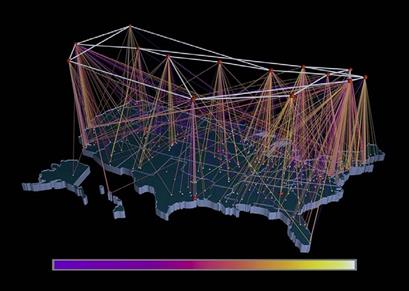
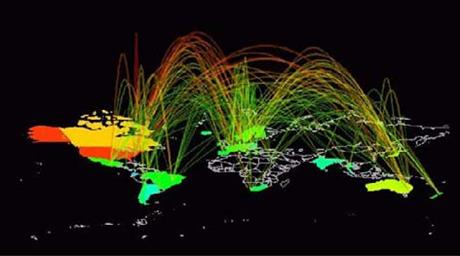
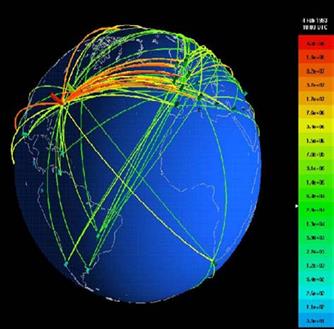
Географічні уявлення

Часто графи використовуються, щоб описати топологію сітей, в яких присутній просторовий або географічний компонент. В цьому випадку, цей компонент використовується, щоб помістити вузли в місце. Наприклад, ми звикли представляти мережі графами, де вузли відповідають фізичному компоненту, сервер, маршрутизатор, центр, і т.д., тоді як краї представляють зв'язки (фізичний або дійсний) серед різних елементів сіті. Часто, у вузлів є широкий масштаб географічного розташування, яке повинне бути зображено візуально. Рис. 2.32 використовує техніку шару, щоб представити географічне освітлення. Основа і зв'язки з різними містами візуально диференційована піднятим шаром географічної карти, щоб створити ясне візуальне розділення між сіттю і територією. Кольоровий масштаб, який йде від фіолетового (нульові байти) білому (100 мільйонів байтів), указує об'єм руху, виміряного в кожному пункті.

Інші приклади топології мережі в світовому масштабі представлені в рис.2.35 SeeNet, як результат роботи Стівена Еіка на Bell Labs. SeeNet візуалізував кількість інтернет-руху усюди по 50 країнам, виміряний за основою NSFNET в 1993. Проте, ці типи уявлень часто цінуються більше для враження від кіберпростору, ніж для їх ефективного використовування

Рис 2.33 Візуалізація яка показує топологію NSFNET T1 базова мережа у вересні 1991 в Сполучених Штатах. Ситуація сьогодні звичайно складніша.

Транспортні мережі

Дуже загальним прикладом інформації, представленої в графічній формі, є сіті портів, представлені на географічній карті, в якій висунуті на перший план міста, зв'язані залізничними лініями. Є, проте, дуже специфічний тип - представлення порту: карти метро. Рис.2.34 показує карту Мадридської сіті метро. Цей тип карти був задуманий в 1931 Гарі Беком, Лондонським службовцем суспільного транспорту, який, в свій вільний час, створив перший проект того, що використовується сьогодні як модель сітей суспільного транспорту у всьому світі. Він запропонував новий тип карти, що була подібна електричними мережами. Його інтуїція повинна була зрозуміти, що мандрівник хоче знати, як досягти призначення, виїжджаючи від певної станції, і не цікавиться фізичним положенням станцій. Що дійсно є топологією сіті, то це як різні станції зв'язані і який маршрут вибрати, щоб швидко досягти певного місця призначення. Таким чином, Мадридська карта Метро, не є "картою" в істинному значенні слова, оскільки пропорції фізичних відстаней між станціями не виражені.

 

Рис 2.35 Тривимірне представлення інтернет-руху через базову мережу NSFNET

Тривимірні Графи

Деякі сучасні інструменти для побудови графів в змозі виробити тривимірне представлення. На Рис.2.36 відображено два приклади, надані програмою Тюльпан, одним з кращих наборів інструментів для того, щоб генерувати графи. Тривимірний граф розташування може бути перетворений і переміщений, щоб дозволити користувачу змінювати уявлення і робити видимий будь-які об'єкти, які можливо могли бути закриті.

 

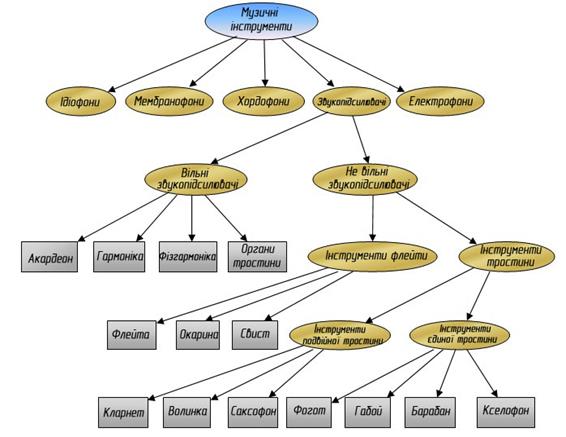
Рис 2.34 Карта Мадридської системи метро.

Ієрархічні Дані

Ми говоримо про ієрархію, розглядаючи дані, що характеризуються базою. Приклади ієрархії в організації файлів, і довідники в комп'ютері (файли містяться в межах довідників, які в свою чергу містяться в межах інших довідників), структура книг (організована в частинах, главах, у графічній формі, організація компанії (президент, директор, радники, спостерігачі, і т.д.), подібні таксономії використовується в біології. Ієрархія може бути представлена через граф із початковим вузлом, названим коренем. У кожного вузла є нуль або більше дитячих вузлів, які звичайно представляються нижче за предка, а предка називають батьківським вузлом.

Рис.2.36 Графи з тривимірними розташуваннями вироблені програмним забезпеченням Тюльпан.

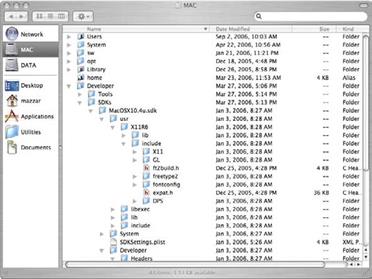
Рис 2.37 Дерево, що представляє класифікацію духових інструментів

У вузла є один батько, графи цього типу визначені як дерева, через їх подібність фактичним деревам, але у відмінності від ботанічних дерев, вони мають корені вгорі а листя в основі. Приклад дерева відтворений на рис 2.37 який представляє спрощену версію класифікації духових інструментів

Файлова система

Для будь-кого, хто витрачає велику частину дня, працюючи з комп'ютерами, знайома ієрархічна структура файлових систем, яка є механізмом, за яким файли зберігаються і організовані на жорсткий диск. У файловій системі файли організовані ієрархічно, починаються з довідника званого коренем, який містить файли або інші довідники. Файлова система може бути представлена через оболонку операційної системи і графічно, через браузер файлу. У візуальному уявленні, що використовується всіма сучасними операційними системами наприклад ієрархія тек рис. 2.22. Проте, це часткове представлення файлової системи, оскільки вона може містити десятки тисяч файлів і довідників. Особливо тим, хто повинен управляти серверами з великими кількостями даних, розділених серед багатьох людей, управління файловою системою, украй важливо. У адміністратора системи повинні бути інструменти, які дозволяють ефективний контроль колекцій файлу на диску, щоб бути в змозі ідентифікувати ситуації, в яких може бути потрібне втручання адміністратора системи.

Рис 2.38 Представлення файлової системи інтерфейсу.

Використовується уявлення з прямокутниками, які поміщені в екран зліва направо. Розташування прямокутників відображає ієрархію файлової системи. Кожен прямокутник відповідає довіднику, і вимірювання прямокутника нанесене на карту до фізичного місця, яке зайняте кожним довідником на диску.

Інші інструменти також робили спробу візуалізації в тривимірній динаміці. Це зробило придатним все більш і більш швидкі тривимірні графічні уявлення на персональних комп'ютерах і можливостями сильних графічних мов, наприклад OpenGL. рис.2.39 який, натомість представляє довідник як "платформа", що підтримує тривимірні блоки, які представляють файли. Візуальне уявлення не повинне нас обманювати: вершини системи адміністрування і професіонали, які управляють файловими системами з великими об'ємами даних, завжди виражали подив про ефективну повноцінність цих типів візуальних уявлень.

Рис 2.39 Використано уявлення файлової системи у вигляді прямокутників.