
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Падение плоской волны на границу поглощающей среды.Содержание книги
Поиск на нашем сайте
Пусть плоская волна падает из идеального диэлектрика на плоскую границу с поглощающей средой. Общие соотношения, полученные для 2-ух идеальных диэлектрических сред применимы и в данном случае т. к. 2-оя Среда является поглощающей, то мы должны предположить, что k2 является комплексной величиной:
Закон Снелиуса применим в любых случаях: т. к. k2 величина комплексная, а k1 и sinj — действительные, то следует предположить, что sin jп — комплексная величина. Т. о. в данном соотношении jп уже нельзя считать геометрическим углом, характеризующим направление распространения преломленной волны. В этом случае удобно ввести следующие обозначения:
Рассмотрим случай перпендикулярной поляризации и запишем выражения для составляющих поля во 2-ой среде:
Из соотношения следует, что в этом случае поле во 2-ой среде представляет собой плоскую волну, у которой поверхность равных фаз не совпадает с поверхностью равных амплитуд:
Это плоская неоднородная не поперечная волна. Направление распространения преломленной волны составляет с осью угол jд (действит.). Учитывая, что фазовый фронт перпендикулярен направлению распространения волны, угол jд можно определить как:
В этом случае поле в 1-ой среде не имеет принципиальных отличий по сравнению со случаем 2-ух идеальных диэлектрических сред. Амплитуда поля во 2-ой среде экспоненциально затухает при удалении от границы раздела. Угол между поверхностью равных фаз и поверхностью равных амплитуд также совпадает с jд. Для дальнейшего обсуждения особо важным является случай, когда: k2>>k1 Обычно это неравенство выполняется, если 2-ая среда является реальным проводником:
В этом случае при любом угле падения j Это означает, что при любом угле j преломленная волна распространяется практически по перпендикуляру к границе раздела. При этом поверхность равных фаз можно считать совпадающей с поверхностью равных амплитуд, т. е. преломленная волна является однородной. Кроме того, при выполнении этого неравенства составляющими поля в направлении распространения преломленной волны можно пренебречь по сравнению с поперечными составляющими, т. е. она является плоской, однородной и поперечной. Т. о. при выполнении этого неравенства преломленную волну можно рассматривать как плоскую волну, существующую в однородном свободном изотропном пространстве с параметрами 2-ой среды. При выполнении этого неравенства преломленная волна существует в тонком приграничном слое. Для реальных металлов:
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.229.217 (0.007 с.) |

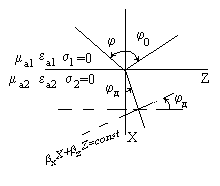
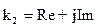 ,
, 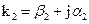 (1)
(1)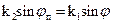 (2)
(2)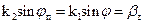 (3)
(3)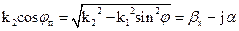 (4)
(4)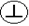
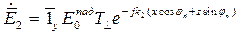 ,
, 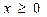 (5)
(5)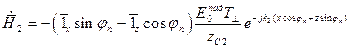 ,
, 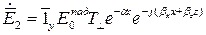 ,
, 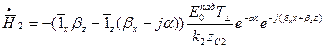 ,
, 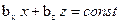 ,
, 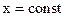 (9)
(9)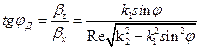 (10)
(10)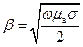 (11)
(11)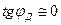 , отсюда
, отсюда 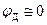 .
.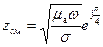 , поэтому между компонентами преломленной волны существует фазовый сдвиг
, поэтому между компонентами преломленной волны существует фазовый сдвиг 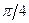 .
.


