
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система уравнений монохроматического (гармонического) поля.
Известно, что уравнения Максвелла относятся к линейным дифференциальным уравнениям. Поэтому в случае гармонических электромагнитных полей в уравнениях Максвелла можно перейти к комплексным амплитудам.
Т.е. если
Используя понятие комплексных амплитуд, получим:
Входящее в соотношение (5) отношение Комплексная диэлектрическая проницаемость в форме (5) справедлива для сред, в которых имеются только джоулевы потери. В общем случае, когда необходимо учесть диэлектрические потери
Этот общий случай позволяет также учесть потери, связанные с эффектом поляризации в переменном электрическом поле. Наличие диэлектрических потерь приводит к появлению фазового сдвига между электрическими векторами D и Е. Величина которого: Переходя во втором уравнении Максвелла к комплексным амплитудам получим:
Магнитные потери связаны с эффектом периодического изменения намагниченности вещества во внешнем поле. Наличие магнитных потерь приводит к фазовому запаздыванию вектора В относительно вектора Н (явление Гистерезиса) в электромагнитных средах. В случае гармонического поля при использовании метода комплексных амплитуд, возникает дополнительная возможность учесть потери, связанные с эффектами поляризации и намагничивания вещества. В случае гармонических полей при использовании метода комплексных амплитуд 3 и 4 уравнения Максвелла являются следствием первых двух. Поясним это: В средах с проводимостью неравной нулю объемная плотность убывает и в случае установившегося электромагнитного процесса (к ним относятся гармонические колебания). Можно считать, что объемная плотность электрического заряда равна нулю. В этом случае третье уравнение Максвелла запишется следующим образом:
Это соотношение для среды с конечной проводимостью. Оно является справедливым и для не проводящих сред. Если в непроводящей среде рассмотрим гармонический процесс, то:
Всякое изменение свободных электрических зарядов сопровождается появлением в среде электрического тока, но при Переходя в уравнении (13) к комплексным амплитудам, получим: Покажем, что оно является следствием (4). Возьмем дивергенцию от правой и левой части. Аналогично и для 4 уравнения Максвелла: В случае гармонических полей они полностью описываются соотношениями (4), (11). Будем предполагать, что в рассмотренной области имеются сторонние источники. В этом случае выражения (4), (11) не применимы. Для получения справедливых соотношений воспользуемся 1 уравнением Максвелла:
Рассмотрим 3 уравнение Максвелла. Возьмем дивергенцию от соотношения (16). Для сторонних токов: В случае гармонических электромагнитных полей мы должны воспользоваться соотношением (17) и (18), при этом (4) и (11) останутся без изменений. Итак, когда имеются сторонние источники:
Уравнения Максвелла без учета сторонних источников:
Подставляя вторую систему в первую, с использованием метода комплексных амплитуд, получим:
В дальнейшем индекс m будем формально опускать.
|
|||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.196 (0.008 с.) |
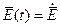
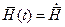
 , то
, то  , где
, где 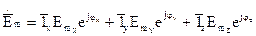
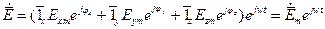 .
.
 (1) т.к.
(1) т.к.  ,
,  (2)
(2) (3)
(3) (4), где
(4), где 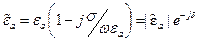 (5)
(5) 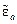 — комплексная диэлектрическая проницаемость среды.
— комплексная диэлектрическая проницаемость среды.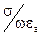 называется тангенсом угла электрических потерь:
называется тангенсом угла электрических потерь:  (6)
(6)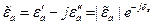 (7)
(7)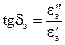 (8) – тангенс угла диэлектрических потерь
(8) – тангенс угла диэлектрических потерь (9)
(9)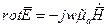 (10).
(10).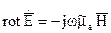 , где
, где  (11)
(11)  (12) — тангенс угла магнитных потерь.
(12) — тангенс угла магнитных потерь.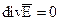 (13)
(13)
 в среде невозможно появление тока удовлетворяющего закону Ома. Поэтому (13) является справедливым в случае гармонических процессов и для непроводящих сред.
в среде невозможно появление тока удовлетворяющего закону Ома. Поэтому (13) является справедливым в случае гармонических процессов и для непроводящих сред. (14)
(14)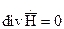 (15)
(15)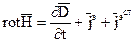
 (16)
(16) 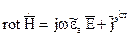 (17)
(17)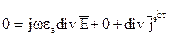
 Окончательно получим:
Окончательно получим: 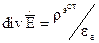 (18)
(18)





