
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электродинамические потенциалы для комплексных амплитуд.Содержание книги
Поиск на нашем сайте
Даже уравнения Максвелла, преобразованные к уравнениям Гельмгольца в форме (5), (8), используются при решении электродинамических задач из-за сложной правой части. При решении задач для векторов поля уравнения используются только для полей без сторонних источников. Обычно, если рассматриваемые задачи со сторонними источниками, используют искусственный прием - вводят формальные поля, которые описываются некоторыми функциями, называемыми электродинамическими потенциалами. Для них решают электродинамическую задачу, а соответствующие вектора электромагнитного поля находят, используя уравнения связи между электромагнитными потенциалами и векторами поля. Получим выражения для электродинамических потенциалов. Для этого запишем уравнения Максвелла:
Существует следующее векторное тождество:
Векторную функцию Подставим (5) в (2). Получим: Воспользуемся вновь тождеством: Скалярную функцию
Помножим на
Формальные поля векторного и электрического потенциалов были введены без ограничений, т.е. это совершенно произвольные функции. Единственное ограничение — это то, что векторное поле электрического потенциала определяется точностью до градиента произвольной функции. Поэтому мы вправе ввести какие-то ограничения. Пусть таким ограничением будет: Равенство (8) называется условием калибровки. А теперь: Аналогичным образом может быть получено выражение для определения скалярного электрического потенциала. Для этого нужно воспользоваться третьим уравнением Максвелла. Вместо
Вместо окончательно получаем:
|
||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.239 (0.007 с.) |

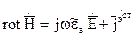 (1)
(1) 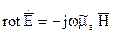 (2)
(2) 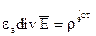 (3)
(3) 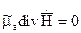 (4)
(4)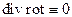 и
и 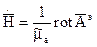 (5)
(5)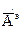 называют векторным электрическимпотенциалом. Соотношение (5) при известном
называют векторным электрическимпотенциалом. Соотношение (5) при известном 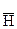 . Обратное определение неоднозначно, т.е. при известном векторном поле
. Обратное определение неоднозначно, т.е. при известном векторном поле 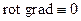 . Поэтому, если ввести
. Поэтому, если ввести 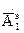 и
и 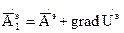 , то соотношение (5) не изменится. Поэтому соотношение (5) определяет
, то соотношение (5) не изменится. Поэтому соотношение (5) определяет 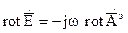 или
или 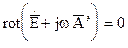 (6)
(6)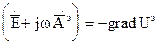 . При этом:
. При этом:  (7)
(7)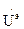 называют скалярным электрическим потенциалом. Знак " - " поставлен, чтобы в случае электростатических полей мы получили соотношение, связывающее напряженность электрического поля и электрический потенциал. С помощью соотношений (5) и (7) определили векторы магнитного и электрического полей через два формальных поля: поля векторного электрического потенциала и поля скалярного электрического потенциала. Получим уравнения для их определения. Подставим соотношения (5) и (7) в первое уравнение Максвелла:
называют скалярным электрическим потенциалом. Знак " - " поставлен, чтобы в случае электростатических полей мы получили соотношение, связывающее напряженность электрического поля и электрический потенциал. С помощью соотношений (5) и (7) определили векторы магнитного и электрического полей через два формальных поля: поля векторного электрического потенциала и поля скалярного электрического потенциала. Получим уравнения для их определения. Подставим соотношения (5) и (7) в первое уравнение Максвелла: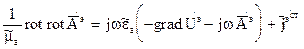
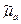 , раскроем
, раскроем 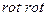 и раскроем скобки.
и раскроем скобки.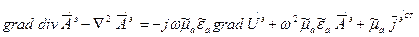
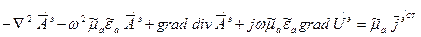
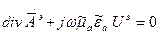 (8)
(8)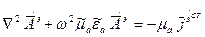 (9)
(9)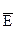 запишем соотношение (7):
запишем соотношение (7):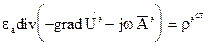
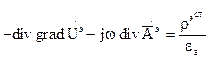
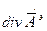 подставим то, чему она равна, используя условие калибровки:
подставим то, чему она равна, используя условие калибровки: 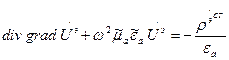
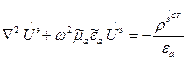 (10)
(10)


