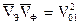Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия возникновения полного внутреннего отражения.Содержание книги
Поиск на нашем сайте
1 условие: 2 условие:
В нашем случае коэффициенты: Для свертки соотношений надо вынести за круглую скобку множитель С учетом проделанных преобразований:
Из полученных соотношений следует: 1. Поле в первой среде является плоской волной. 2. Поверхности равных фаз образуют семейство плоскостей, перпендикулярных оси Z, т.е. определяется уравнением Z=const. 3. Амплитуда плоских волн зависит от угла падения j и координаты Х. 4. Поверхность равных амплитуд определяется уравнением X=const. 5. Поверхность равных амплитуд не совпадает с поверхностью равных фаз. 6. Плоские волны являются неоднородными. 7. Плоские волны в первой среде распространяются вдоль оси Z, т.е. вдоль границы раздела, такие волны называются направляемыми. И в случае перпендикулярной и параллельной поляризации плоские волны имеют составляющую поля в направлении распространения (в случае перпендикулярной поляризации Нz, в случае параллельной поляризации Ez), т.е. полученные решения представляют собой плоскую, неоднородную, не поперечную волну. Определим фазовую скорость. Общее выражение: Проанализируем:
Из выражения (9) видно, что направляющая волна распространяется с фазовой скоростью, которая превышает фазовую скорость плоской волны в свободном пространстве с параметрами первой среды, но меньше фазовой скорости в свободном пространстве с параметрами второй среды. Определяем длину волны в направлении распространения: Из соотношений при
Глядя на эти же соотношения, можно отметить, что поперечные, относительно направления распространения поля, компоненты поля ( Определим энергетические параметры. Определим комплексный вектор Пойнтинга:
В выражении (12) знак "+" соответствует нормальной поляризации, а знак "-" для параллельной поляризации. Как следует из (12) комплексный вектор Пойнтинга имеет реальную и мнимую части.
Среднее за период значение вектора Пойнтинга направлено вдоль оси Z.
Т.е. в среднем за период энергия переносится вдоль оси Z. В направлении, перпендикулярном границе раздела существует реактивный поток мощности. Из (*) видно, что имеется бесконечное количество плоскостей, перпендикулярных оси Х (параллельных границе раздела), в которых Еt и Нn обращаются в нуль. Точки пересечения этих плоскостей с осью Х можно определить из следующего соотношения:
В случае параллельной поляризации, параллельной границе раздела, будет параллельна и компонента Еz. Из предыдущего соотношения следует:
где n=1, 2, 3,... Из приведенных рассуждений следует, что в плоскостях, параллельных границе раздела, положение которых описывается в (14), автоматически удовлетворяет граничные условия, соответствующие граничным условиям на поверхности идеального проводника (Еt=0, Нn=0). Если мы одну из этих плоскостей заменим идеально проводящей поверхностью (Хn), то получим, что при
Еще характерная особенность этих плоскостей (14) заключается в том, что поток энергии через эти поверхности (как активной, так и реактивной) равна нулю. Определим среднее за период значение скорости распространения энергии в первой среде. В первой среде при В качестве энергетической трубки удобно взять часть пространства, ограниченное соседними поверхностями, положение которых определяется (14). Например, Xn, Xn+1. В этом случае, учитывая, что составляющая поля зависит от координаты Х, выражение для скорости распространения энергии включает обязательно интегрирование. Подставляя соответствующие компоненты и осуществляя интегрирование, получим:
Выражение для фазовой скорости:
|
|||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

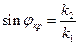 так как sinj<1 то k2<k1 Вторая среда должна быть оптически менее плотная, чем первая
так как sinj<1 то k2<k1 Вторая среда должна быть оптически менее плотная, чем первая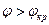 Получим выражение для структуры поля, результирующей волны в первой среде при
Получим выражение для структуры поля, результирующей волны в первой среде при 
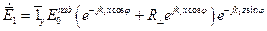 ,
, 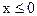
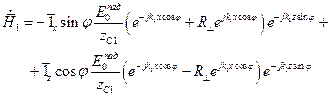 ,
, 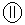
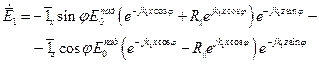 ,
, 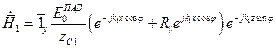 ,
, 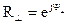 ,
, 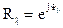
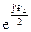 .
.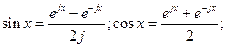
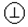
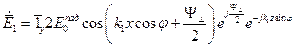 ,
, 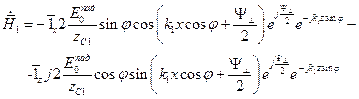 ,
, 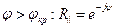
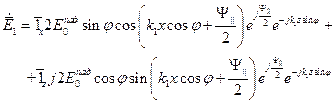 ,
, 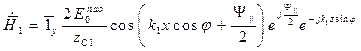 ,
, 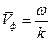 В нашем случае:
В нашем случае: 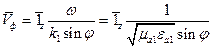
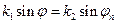 при
при 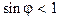 ;
; 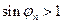
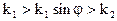 ,
, 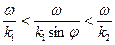
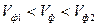 (9)
(9)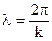 Или в данном случае:
Или в данном случае: 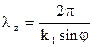 (10)
(10) 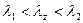 (11)
(11)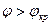 следует, что в направлении, перпендикулярном границе раздела (параллельной оси Х), поле имеет характер стоячей волны с пространственным периодом или длинной волны.
следует, что в направлении, перпендикулярном границе раздела (параллельной оси Х), поле имеет характер стоячей волны с пространственным периодом или длинной волны. 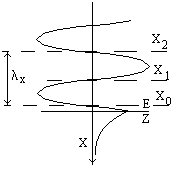
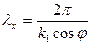
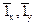 )—синфазны. Продольная, относительно поперечных, имеет фазовый сдвиг 90 (Z).
)—синфазны. Продольная, относительно поперечных, имеет фазовый сдвиг 90 (Z).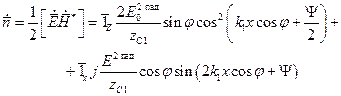 (12)
(12)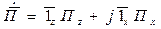
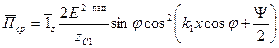 (13)
(13)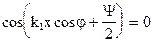
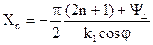 (14)
(14)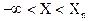 (т.е. над плоскостью в первой среде) поле останется неизменным.
(т.е. над плоскостью в первой среде) поле останется неизменным.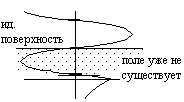
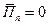 .
.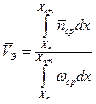 (15)
(15)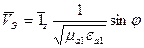 (16)
(16)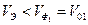
 Из (16) видно, что скорость распространения энергии в первой среде меньше скорости света в первой среде.
Из (16) видно, что скорость распространения энергии в первой среде меньше скорости света в первой среде.